Two-step Equations Math Worksheets
If you are a math teacher or a parent looking to reinforce the concept of two-step equations with your students or child, then these two-step equations math worksheets are the perfect resource for you. This collection of worksheets is designed to help solidify understanding and improve problem-solving skills by providing a variety of practice problems involving two-step equations.
Table of Images 👆
- Math Expressions Worksheets 7th Grade
- 8th Grade Algebraic Equations Worksheets
- Two-Step Inequalities Worksheets
- Algebra 1 Step Equation Problems Worksheets
- One Step Equations Worksheets
- 4th Grade Math Worksheets Fractions
- Two-Step Equation Word Problems Worksheets
- Multi-Step Equations Worksheets
- Multi-Step Equations
- Math Problem Solving Steps Worksheet
- Algebra Math Worksheets Printable
- 7 Grade Math
- Common Core Grade 7 Math Worksheets
- 4th Grade Multiplication Comparison Problems
- Algebra Solving Multi-Step Equations Worksheet
More Math Worksheets
Printable Math WorksheetsMath Worksheets Printable
Printable Math Worksheets Multiplication
Math Worksheets for 2nd Graders
Math Practice Worksheet Grade 6
Math Multiplication Worksheets
First Grade Subtraction Math Worksheets Printable
Rocket Math Practice Worksheets
Math Worksheets Integers
Superhero Math Worksheets
What is a two-step equation?
A two-step equation is an algebraic equation that requires two different operations to solve for the variable. This typically involves applying inverse operations such as addition or subtraction, followed by multiplication or division, to isolate the variable on one side of the equation.
How do you represent a two-step equation mathematically?
A two-step equation can be represented mathematically as \( ax + b = c \), where \(a\), \(b\), and \(c\) are constants and \(x\) is the variable unknown that needs to be solved for. The equation involves two operations that need to be performed in sequence to isolate the variable \(x\), such as adding or subtracting a constant term and then multiplying or dividing by a coefficient.
What is the purpose of solving a two-step equation?
The purpose of solving a two-step equation is to find the value of the variable in the equation by performing a sequence of two mathematical operations. By solving a two-step equation, we can determine the specific value of the unknown variable that satisfies the given equation, helping us to understand and analyze various mathematical and real-world problems involving relationships between different quantities.
What are the two steps involved in solving a two-step equation?
The two steps involved in solving a two-step equation are: 1) Perform the operation that is furthest away from the variable to isolate the variable on one side of the equation. 2) Perform the inverse operation to isolate the variable and solve for its value.
How do you apply the addition or subtraction property of equality in two-step equations?
In two-step equations, you apply the addition or subtraction property of equality by first isolating the variable term. To do this, you add or subtract the constant term from both sides of the equation in order to get the variable term by itself on one side of the equation. This allows you to easily solve for the variable by performing the necessary operations while keeping the equation balanced.
How do you apply the multiplication or division property of equality in two-step equations?
To apply the multiplication property of equality in two-step equations, you can multiply or divide both sides of the equation by the same non-zero number to isolate the variable on one side. For example, if you have the equation 3x - 5 = 10, you can first add 5 to both sides to get 3x = 15. Next, you can multiply both sides by 1/3 to find the value of x. The division property of equality works in a similar way, where you divide both sides of the equation by the same non-zero number to isolate the variable.
Can you provide an example of a two-step equation and its solution?
Sure! An example of a two-step equation is 3x + 7 = 16. First, we subtract 7 from both sides to isolate the variable: 3x = 9. Then, we divide both sides by 3 to solve for x: x = 3. So, the solution to the equation 3x + 7 = 16 is x = 3.
Are there any special cases or exceptions in solving two-step equations?
In solving two-step equations, there are no specific special cases or exceptions to keep in mind. The main idea is to isolate the variable by performing inverse operations to both sides of the equation until the variable is alone. Just remember to follow the order of operations and be careful with signs when combining like terms.
How can you check if a solution to a two-step equation is correct?
To check if a solution to a two-step equation is correct, you can substitute the solution back into the original equation and solve for both sides of the equation to see if the values are equal. If they are, then the solution is correct.
Are there any real-life applications of two-step equations?
Yes, two-step equations have numerous real-life applications. They are commonly used in various fields such as finance for calculating interest rates and loan payments, in engineering for determining forces and velocities, in physics for solving motion and energy problems, and in chemistry for calculating reaction rates and concentrations. Additionally, two-step equations are also used in everyday scenarios such as budgeting, recipe conversions, and HVAC system calculations. Overall, understanding and solving two-step equations is essential for problem-solving in a wide range of professions and daily life situations.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






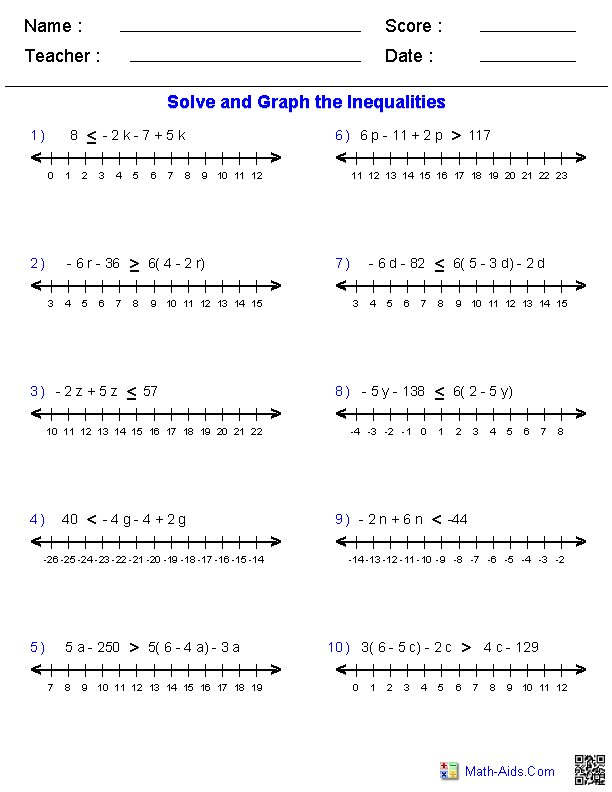

























Comments