Trigonometry Worksheets and Answers PDF

Trigonometry worksheets provide a valuable resource for students looking to strengthen their understanding of this mathematical subject. These worksheets cover various topics within trigonometry, including angles, functions, and equations. With clear instructions and detailed solutions, they offer a comprehensive learning experience for high school and college students studying trigonometry.

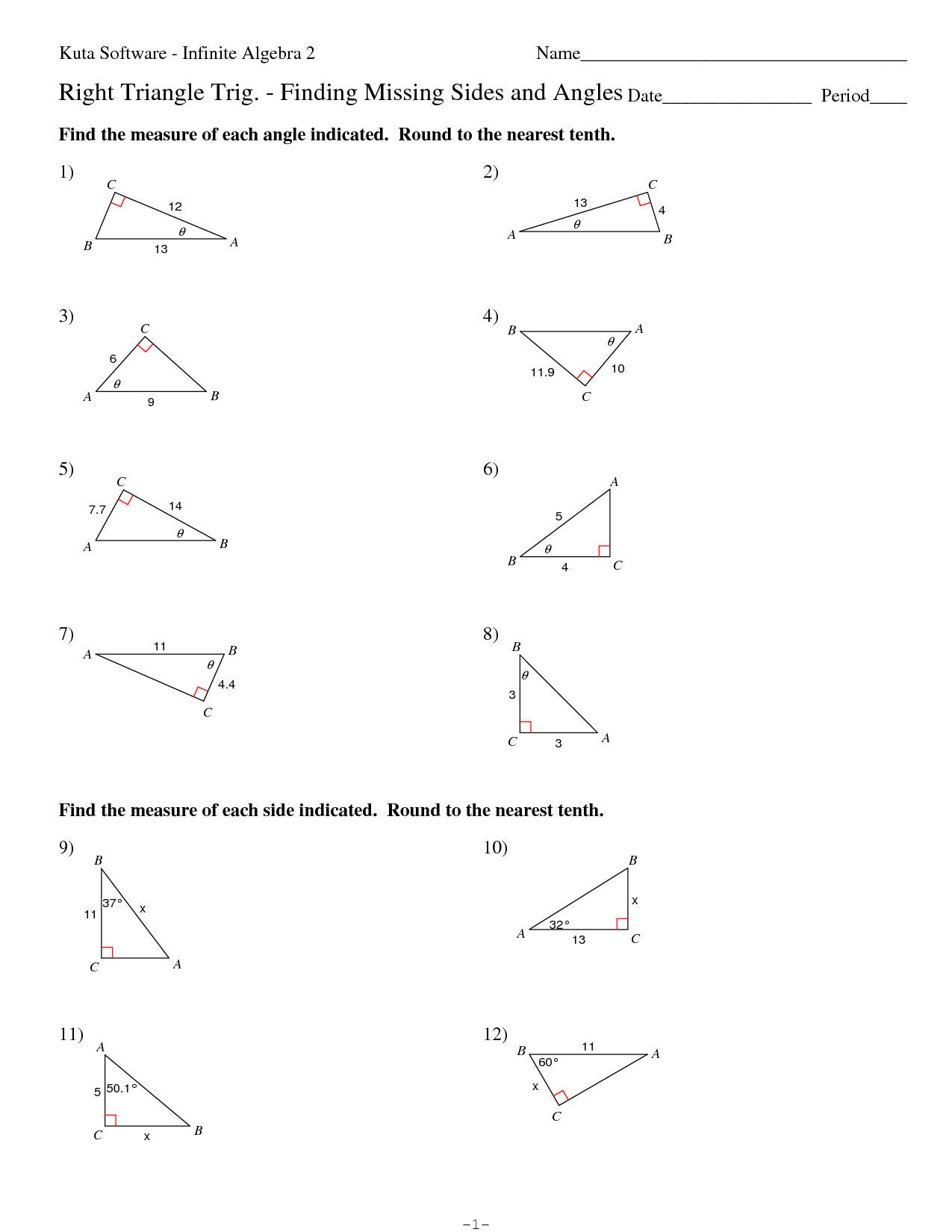
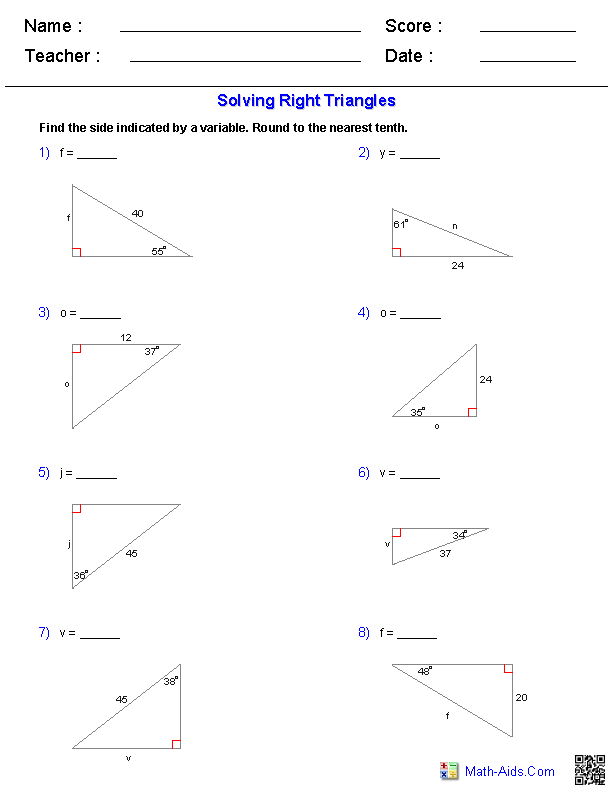
  Right Triangle Trigonometry Worksheet

---

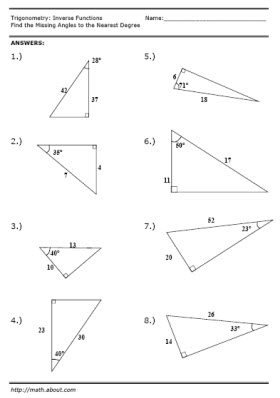
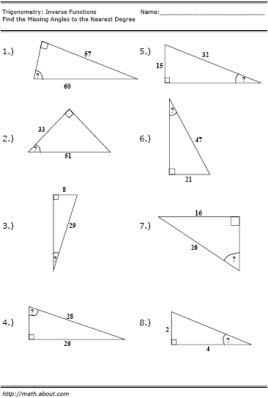
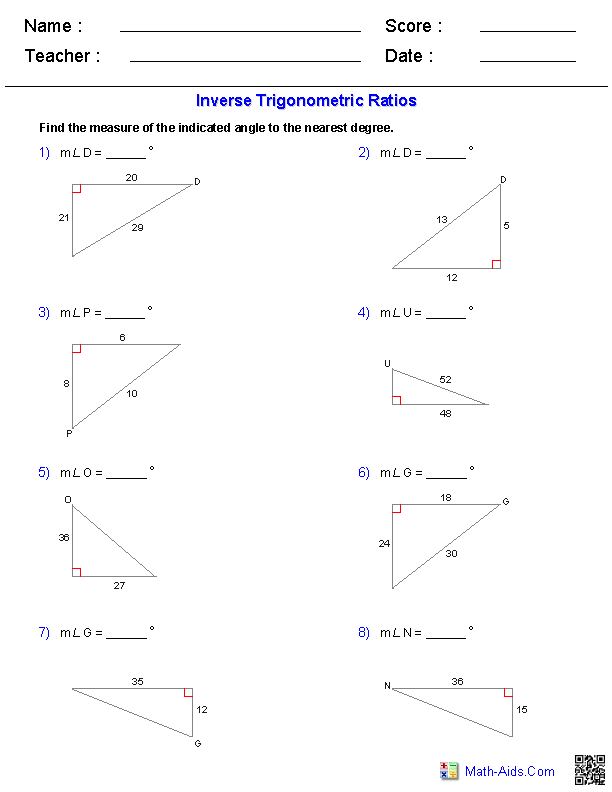
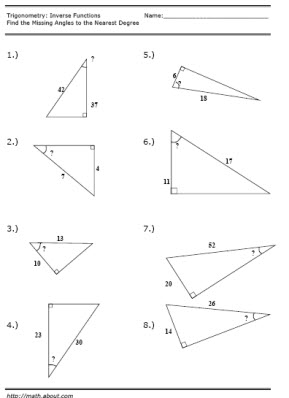
  Inverse Trig Functions Worksheet

---

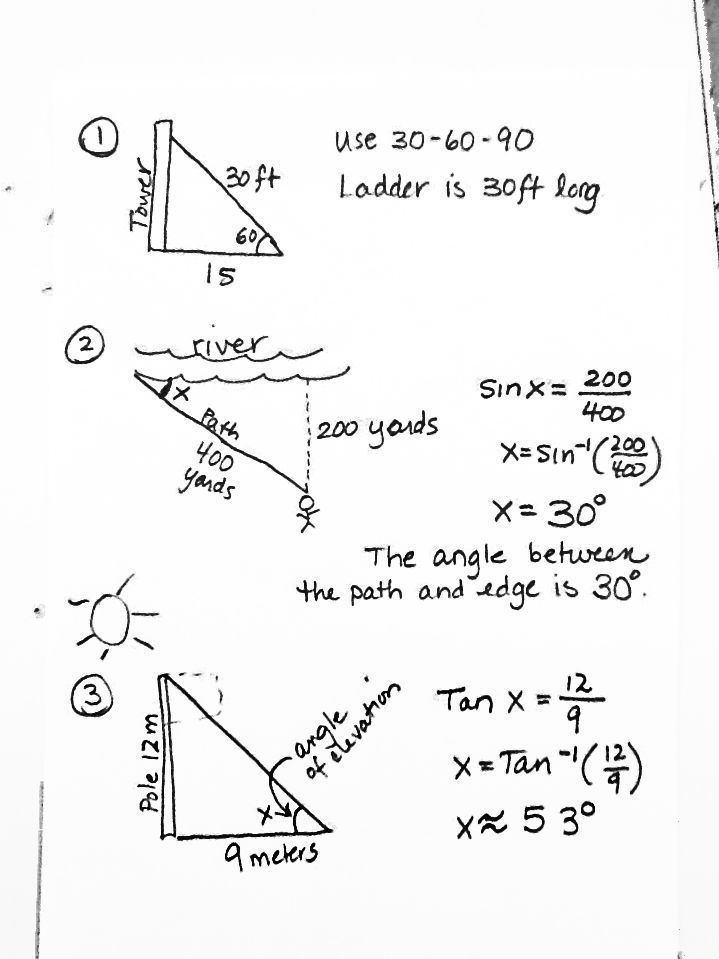
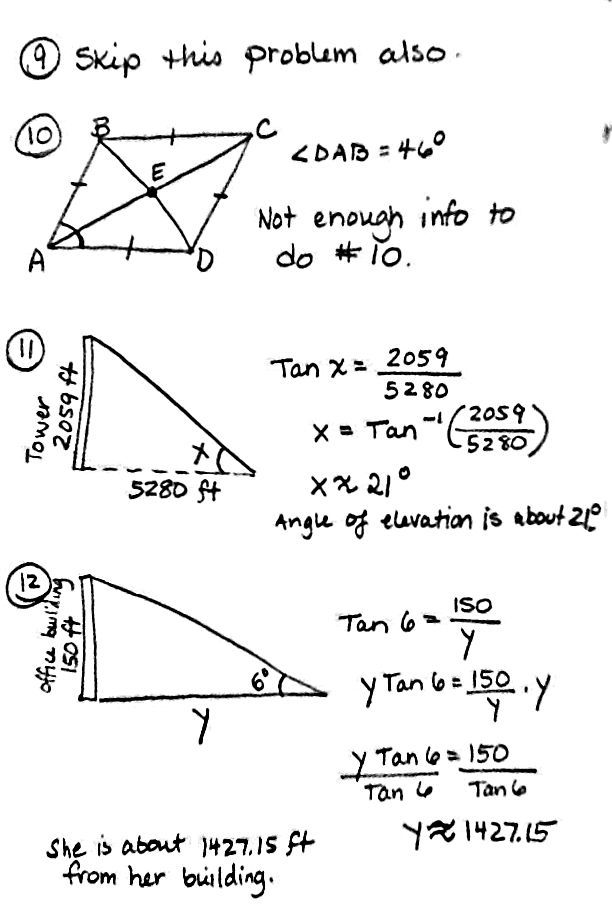
  Right Triangle Trigonometry Word Problems Worksheets

---

  Right Triangle Trigonometry Worksheet

---

  Inverse Trig Functions Worksheet

---

  Free Printable Trigonometry Worksheets

---

  Special Right Triangles Worksheet Answers

---

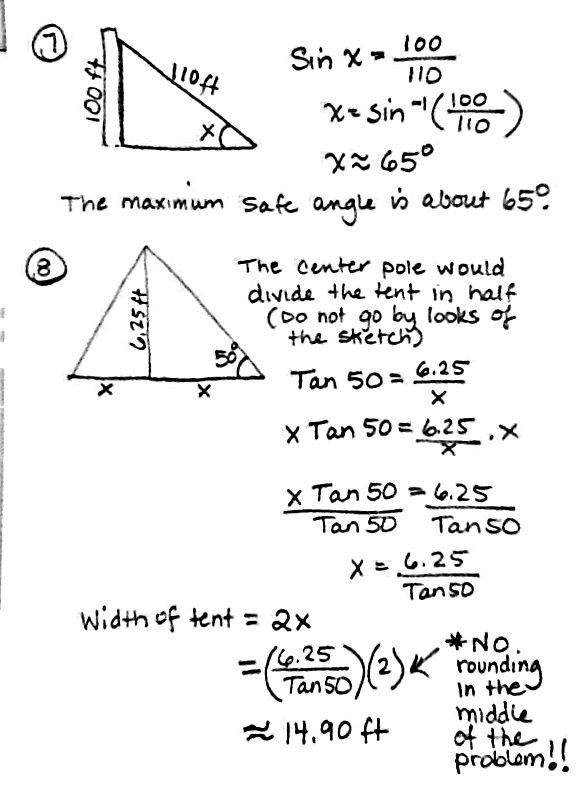
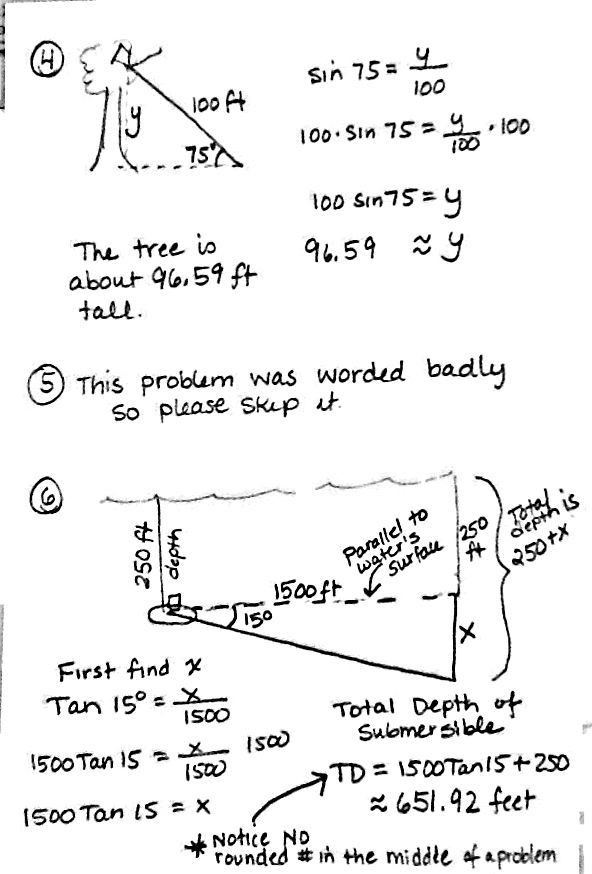
  Right Triangle Trig Word Problems Worksheet

---

  Right Triangle Word Problems Worksheet

---

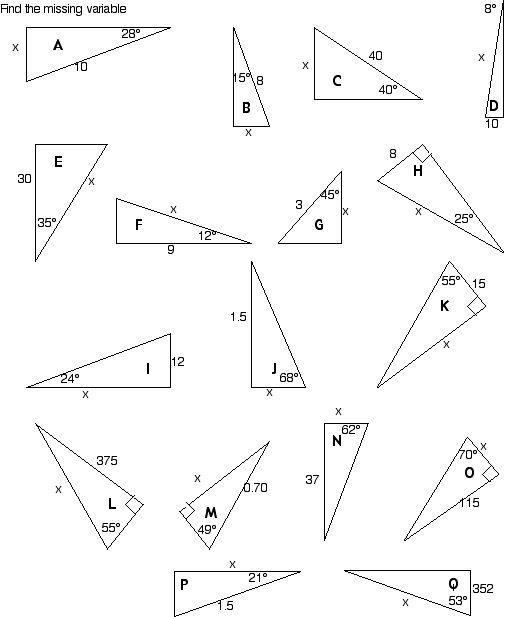
  Trigonometric Ratios Worksheets

---

  Inverse Trig Functions Worksheet

---

  Trig Unit Circle Worksheet

---

  Right Triangle Word Problems Worksheet

---

  Basic Trigonometry Worksheet

---

  Trigonometry Sin Cos Tan Worksheets

---

  Inverse Trigonometry Functions Worksheets

---

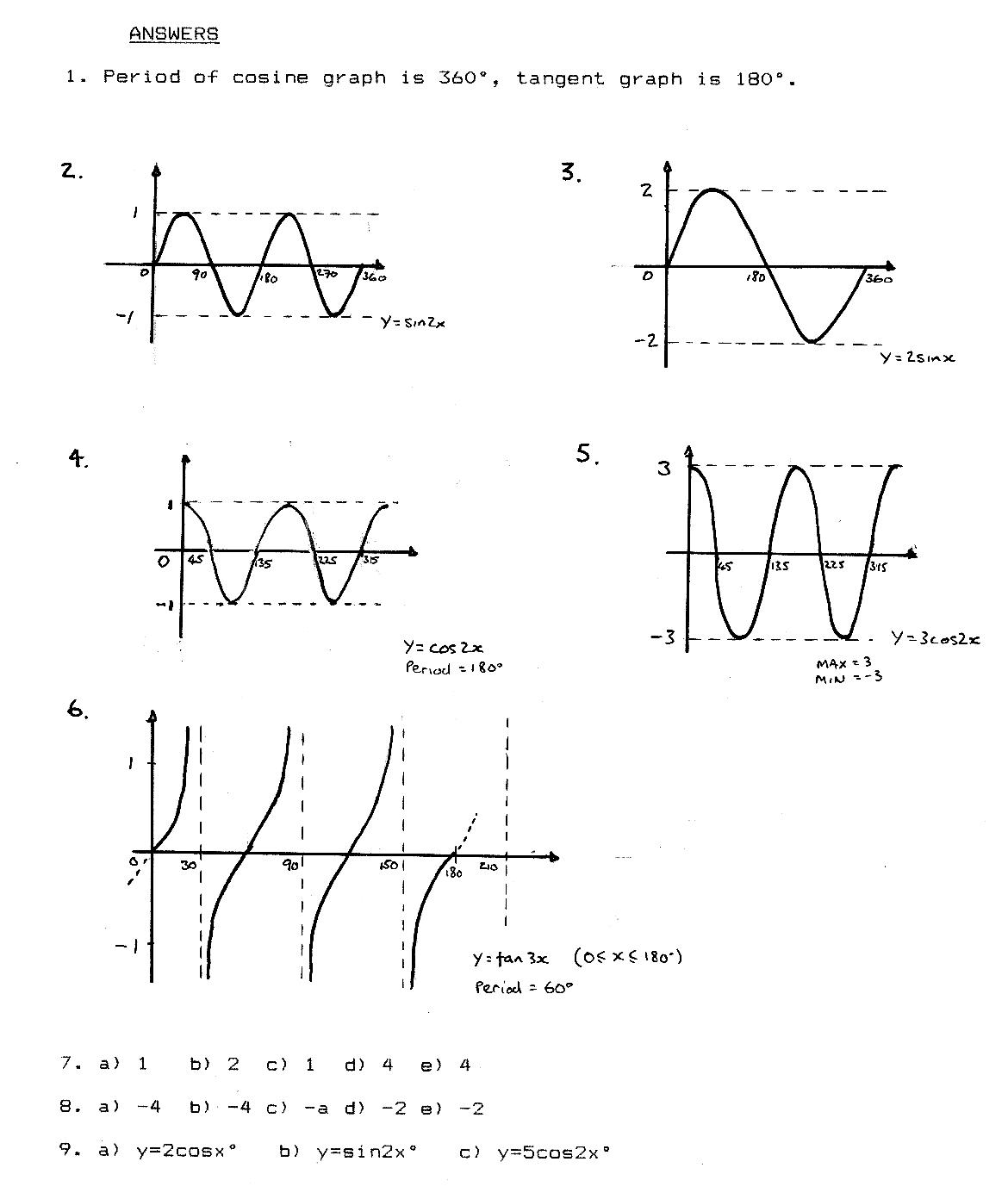
  Graph Trig Functions Worksheet

---

  Trig Identity Cheat Sheet

---

What is Trigonometry?

Trigonometry is a branch of mathematics that focuses on the relationships between the angles and sides of triangles. It involves studying the properties and functions of triangles, such as sine, cosine, and tangent, to solve problems related to angles, distances, and heights. Trigonometry is commonly used in fields like engineering, physics, and astronomy to analyze and understand various phenomena involving angles and distances.

What are the basic trigonometric functions?

The basic trigonometric functions are sine, cosine, and tangent. These functions relate the angles of a right triangle to the lengths of its sides, with sine representing the ratio of the length of the opposite side to the hypotenuse, cosine representing the ratio of the length of the adjacent side to the hypotenuse, and tangent representing the ratio of the length of the opposite side to the adjacent side.

How are sine, cosine, and tangent related to right triangles?

Sine, cosine, and tangent are trigonometric functions that relate the angles of a right triangle to the lengths of its sides. In a right triangle, the sine of an angle is the ratio of the length of the side opposite the angle to the hypotenuse, the cosine is the ratio of the length of the adjacent side to the hypotenuse, and the tangent is the ratio of the length of the opposite side to the adjacent side. These functions are fundamental in trigonometry for solving problems related to right triangles and other geometric shapes.

How can trigonometry be applied in real-life situations?

Trigonometry can be applied in various real-life situations such as architecture for designing buildings, engineering for calculating forces and angles in structures, physics for analyzing motion and waves, astronomy for studying celestial bodies, and navigation for determining distances and directions. It is also used in surveying land, designing video games, analyzing sound waves in music and sound engineering, and in medical imaging for creating detailed images of the human body.

How can the unit circle be used to solve trigonometric equations?

The unit circle can be used to solve trigonometric equations by visualizing the relationship between the coordinates of a point on the unit circle and the values of sine and cosine for different angles. By understanding the properties of the unit circle, one can easily determine the values of trigonometric functions for specific angles and use them to solve equations involving trigonometric functions. This method helps in simplifying calculations and providing geometric insight into the solutions of trigonometric equations.

What are the identities and formulas used in trigonometry?

In trigonometry, some common identities and formulas include: sine: sin(?) = opposite/hypotenuse, cosine: cos(?) = adjacent/hypotenuse, tangent: tan(?) = opposite/adjacent, Pythagorean theorem: a^2 + b^2 = c^2, sum and difference formulas, double angle formulas, half angle formulas, and law of sines and cosines. These identities and formulas are essential for solving trigonometric equations and proving various mathematical relationships in triangles and circles.

What is the Law of Sines and how is it used?

The Law of Sines is a trigonometric formula that relates the lengths of the sides of a triangle to the sines of its angles. It states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is constant for all three sides and angles in a triangle. This law is used to solve triangles when given certain combinations of side lengths and angle measures, particularly in cases where not all three sides are known. By using the Law of Sines, we can find missing side lengths or angles in a triangle.

What is the Law of Cosines and how is it used?

The Law of Cosines is a mathematical formula used to find the length of a side or measure of an angle in a triangle when the lengths of the other two sides and the angle between them are known. It is particularly useful for solving triangles that are not right-angled. The formula is c^2 = a^2 + b^2 - 2ab * cos(C), where c is the length of the unknown side, a and b are the lengths of the other two sides, and C is the angle opposite to side c. This law is used in trigonometry and geometry to calculate unknown triangle measurements.

How can trigonometric functions be graphed?

Trigonometric functions can be graphed by plotting points based on the values of the function at various angles within the unit circle, where the x-coordinate represents the cosine value and the y-coordinate represents the sine value. By connecting these points smoothly, the graph of the trigonometric function can be visualized, showing the periodic behavior of the function over a specific domain. Additionally, knowing the fundamental properties of trigonometric functions like amplitude, period, and phase shift, can help accurately graph them on coordinate axes.

What are some common trigonometric identities and their applications?

Some common trigonometric identities include the Pythagorean identity (sin^2(theta) + cos^2(theta) = 1), the even and odd identities (sin(-theta) = -sin(theta), cos(-theta) = cos(theta)), and the double angle identities (sin(2theta) = 2sin(theta)cos(theta), cos(2theta) = cos^2(theta) - sin^2(theta)). These identities are essential in simplifying trigonometric expressions, solving trigonometric equations, and proving mathematical statements in calculus, physics, engineering, and other fields that involve periodic functions and angles.