Trigonometry Trig Worksheets

Trigonometry Trig worksheets are a helpful tool for students who are studying or reviewing trigonometric concepts. These worksheets provide a focused and structured approach to learning about the various entities and subjects within the field of trigonometry. Designed to reinforce key principles and provide practice opportunities, trig worksheets offer a comprehensive resource for students seeking to improve their understanding and proficiency in trigonometry.

  Free Printable Trigonometry Worksheets

---

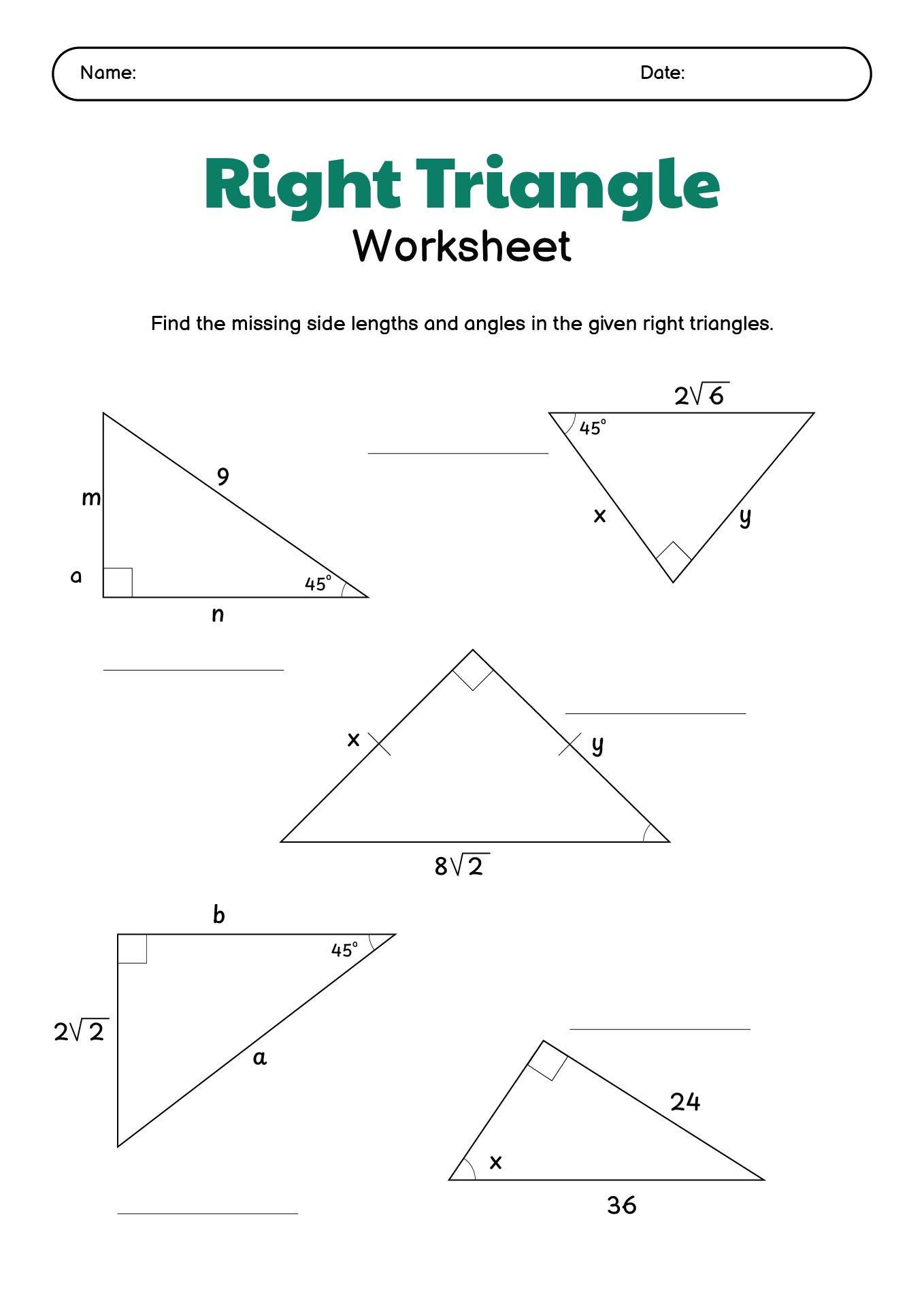
  Right Triangle Trigonometry Worksheet

---

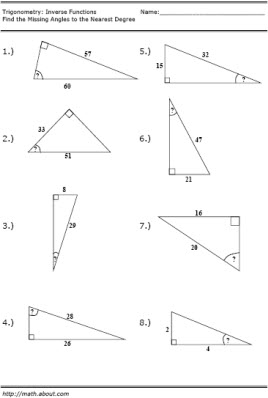
  Inverse Trig Functions Worksheet

---

  Trig Identities Worksheet

---

  Derivative Inverse Trig Functions Worksheet

---

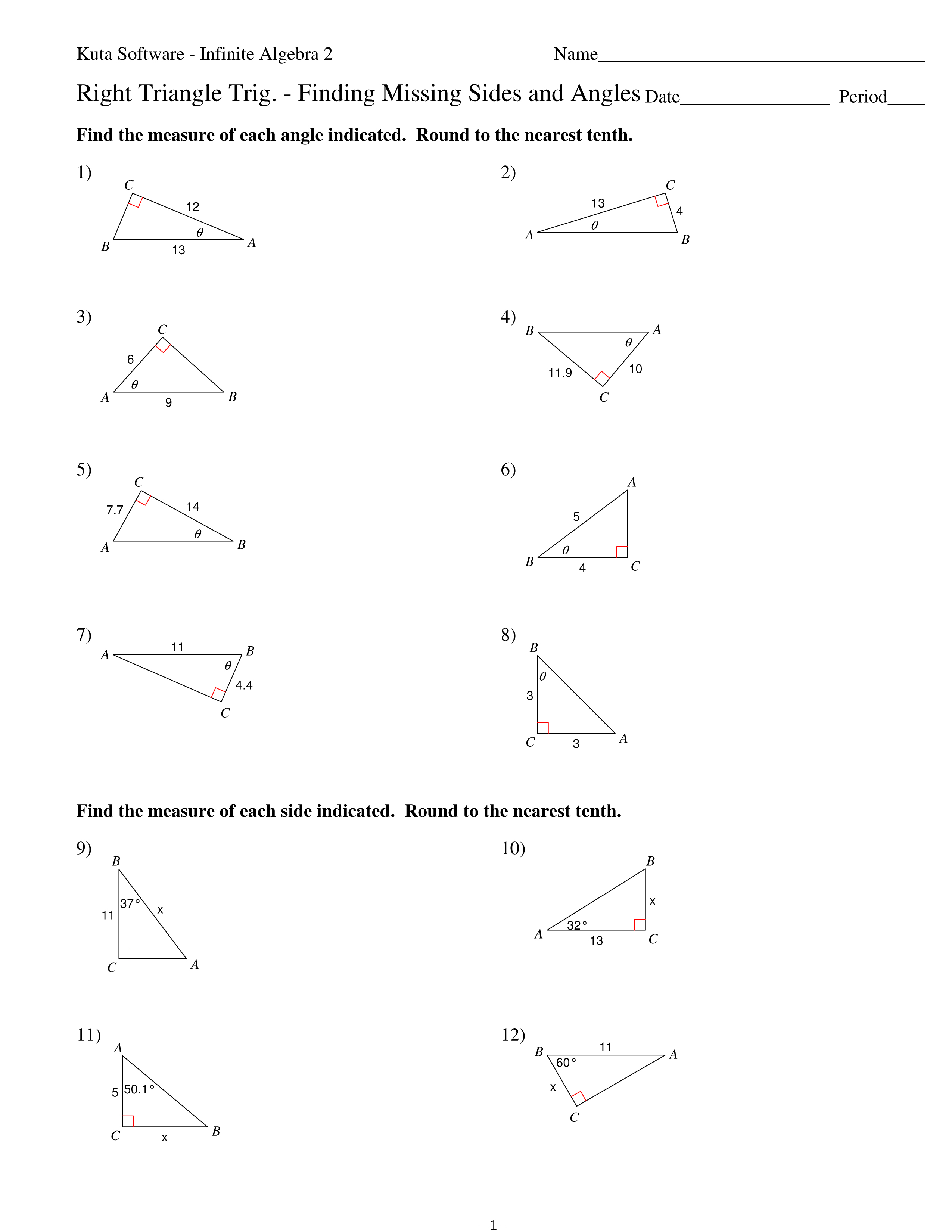
  Trig Right Triangles Missing Angles and Sides

---

  Flag Pole Heights for Buildings

---

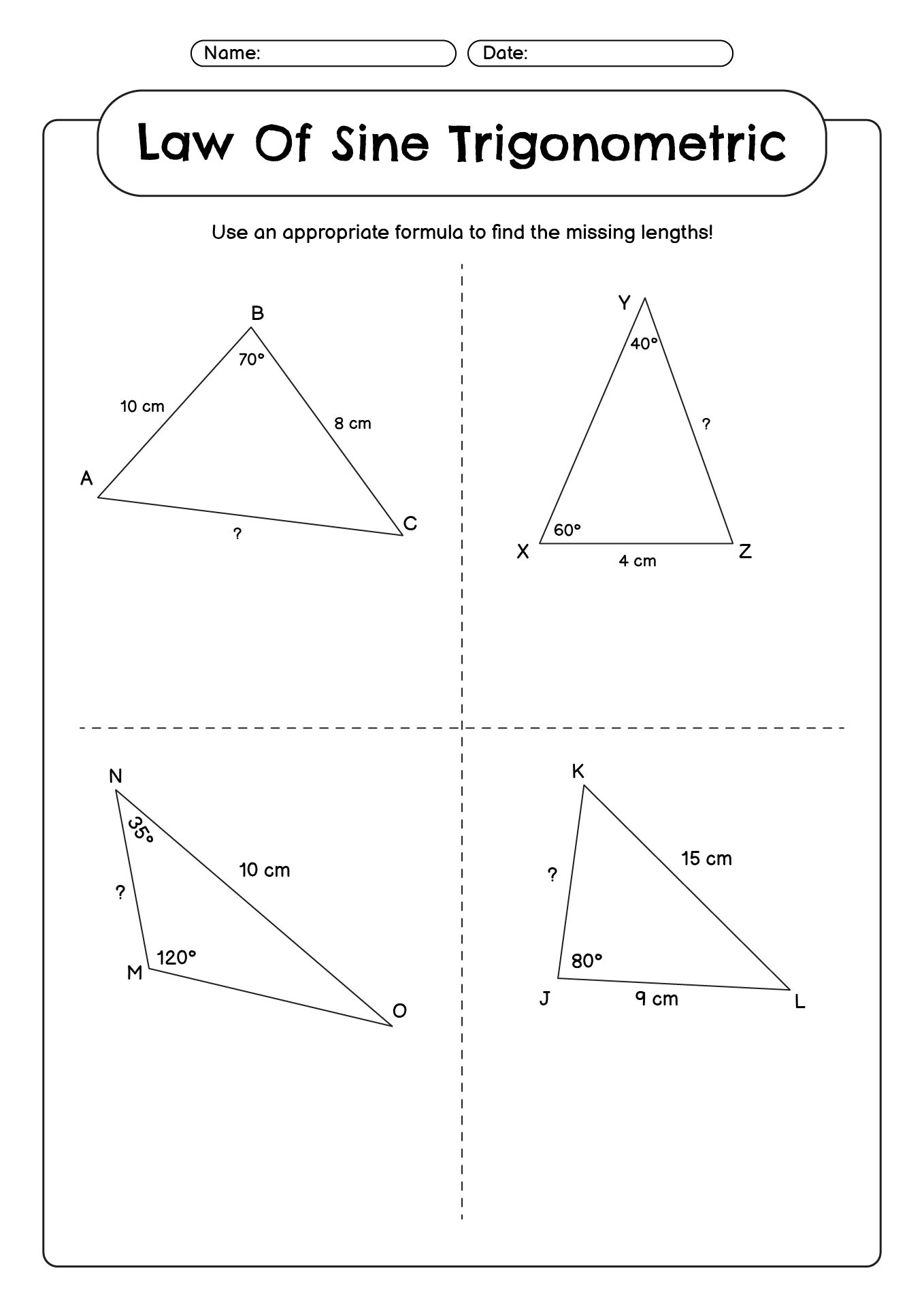
  Law of Sine Trigonometric Functions

---

  Blank Trig Graph Paper Radians

---

  Circle Graph Worksheets 8th Grade

---

  Trigonometry Homework Sheets

---

  Geometry Trig Ratios Worksheet

---

  Geometry Trig Ratios Worksheet

---

  Geometry Trig Ratios Worksheet

---

What is the sine of an acute angle in a right triangle?

The sine of an acute angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is calculated by dividing the length of the side opposite the angle by the length of the hypotenuse.

How is the tangent of an angle defined?

The tangent of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. In terms of trigonometry, the tangent of an angle ? is equal to the opposite side length divided by the adjacent side length, which can be represented as tan(?) = oppositie/adjacent.

What is the relationship between the cosine of an angle and its adjacent side?

The cosine of an angle in a right triangle is equal to the length of the adjacent side divided by the length of the hypotenuse. This means that the cosine function relates the adjacent side of a right triangle to the angle formed by that side and the hypotenuse.

What does the Pythagorean Identity state in Trigonometry?

The Pythagorean Identity in trigonometry states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. It is expressed as \( \sin^2(\theta) + \cos^2(\theta) = 1 \), where \( \theta \) is the angle in the right triangle.

How is the angle of elevation or depression calculated?

The angle of elevation or depression is calculated by measuring the angle formed between a horizontal line and the line of sight to an object above (elevation) or below (depression) the horizontal line. This angle can be measured using a clinometer or by using trigonometric functions such as tangent, sine, or cosine when the distance to the object and the height difference are known.

What is the purpose of the Law of Sines in Trigonometry?

The Law of Sines in Trigonometry is used to solve triangles that are not right-angled. It relates the lengths of the sides of a triangle to the sines of its angles, allowing us to find missing side lengths or angles given certain information. This law is particularly useful in navigation, surveying, and other real-world situations where non-right triangles are encountered.

How is the Law of Cosines useful in solving triangles?

The Law of Cosines is useful in solving triangles because it allows us to find the lengths of sides and measures of angles in non-right triangles. By using the formula c^2 = a^2 + b^2 - 2ab cos(C), where c is the unknown side and C is the unknown angle opposite that side, we can solve for missing sides or angles in a triangle. This is particularly helpful when dealing with oblique triangles where we do not have a right angle to apply the Pythagorean theorem.

What is the unit circle and how is it used in Trigonometry?

The unit circle is a circle with a radius of 1 centered at the origin of a coordinate system. In trigonometry, the unit circle is used to define the values of trigonometric functions for all angles. By associating each point on the unit circle with an angle, trigonometric functions like sine, cosine, and tangent can be calculated for any angle by examining the coordinates of the corresponding point on the circle. This helps in simplifying trigonometric calculations and visualizing relationships between angles and trigonometric ratios.

How are trigonometric functions extended to include any angle?

Trigonometric functions are extended to include any angle by using the unit circle and periodicity. By defining the trigonometric functions sine and cosine on the unit circle, we can associate any angle with a point on the circle. From there, we can use periodicity to extend these functions to any angle by repeating the values of the functions at regular intervals. This allows us to calculate trigonometric functions for angles beyond 0 to 360 degrees or 0 to 2? radians, making them applicable to any angle in the Cartesian coordinate system.

What are the reciprocal trigonometric functions and how are they defined?

The reciprocal trigonometric functions are secant, cosecant, and cotangent. They are defined as the reciprocals of the cosine, sine, and tangent functions respectively. Specifically, secant(theta) = 1/cos(theta), cosecant(theta) = 1/sin(theta), and cotangent(theta) = 1/tan(theta). These functions are commonly used in trigonometry to calculate the lengths of sides in right triangles and to solve trigonometric equations.