Trig Identities Worksheet

The Trig Identities Worksheet is an essential tool for high school and college students studying trigonometry. This worksheet provides a comprehensive practice on the different trigonometric identities and their applications. Designed to reinforce understanding and sharpen skills, the Trig Identities Worksheet is perfect for students seeking additional practice on this subject.

  Trig Identities Equations

---

  Basic Trig Functions Worksheet

---

  Math Algebra Cartoons Equations

---

  Trig Identities Cheat Sheet for Precalculus

---

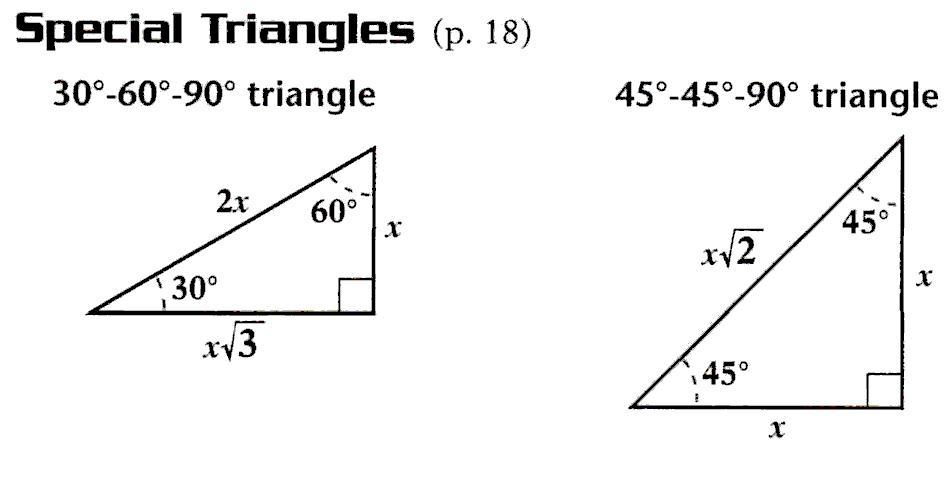
  Special Triangles Formulas

---

  Trigonometry Ratio Worksheets

---

  Trigonometry Ratio Worksheets

---

  Trigonometry Ratio Worksheets

---

  Trigonometry Ratio Worksheets

---

  Trigonometry Ratio Worksheets

---

  Trigonometry Ratio Worksheets

---

What is the definition of a trigonometric identity?

A trigonometric identity is an equation involving trigonometric functions that is true for all values of the variables within its domain. These identities are used to simplify expressions, prove mathematical theorems, and solve equations in trigonometry. Key identities include the Pythagorean identities, sum and difference identities, double angle identities, and half-angle identities.

What is the Pythagorean identity and how is it used?

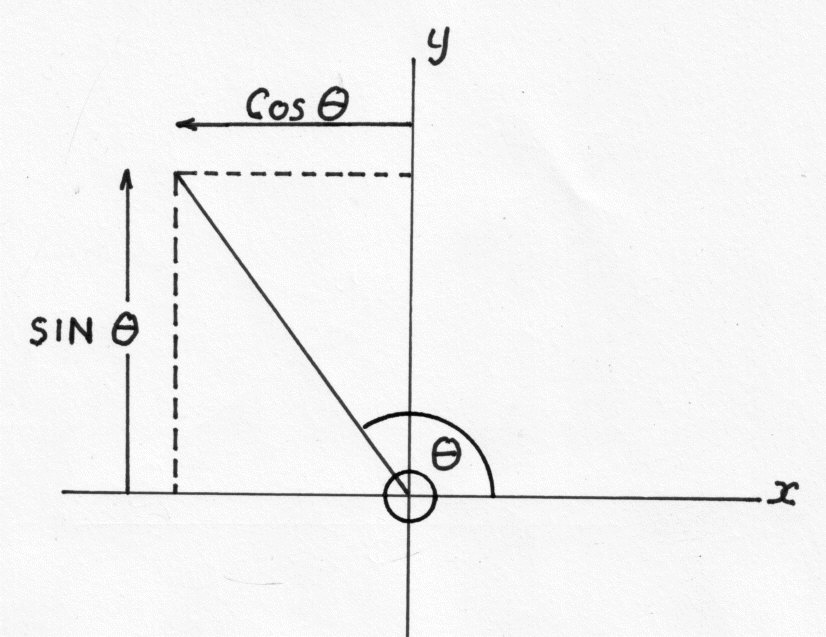
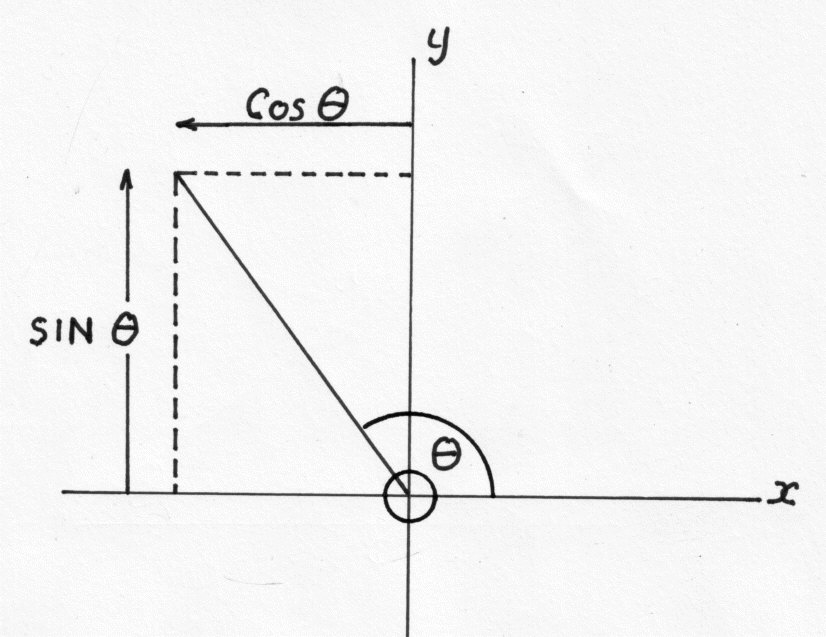
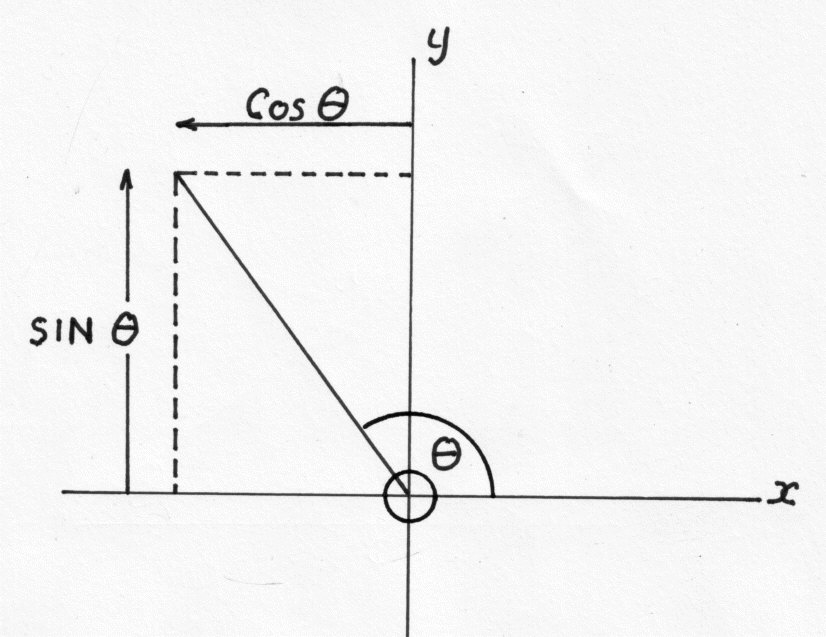
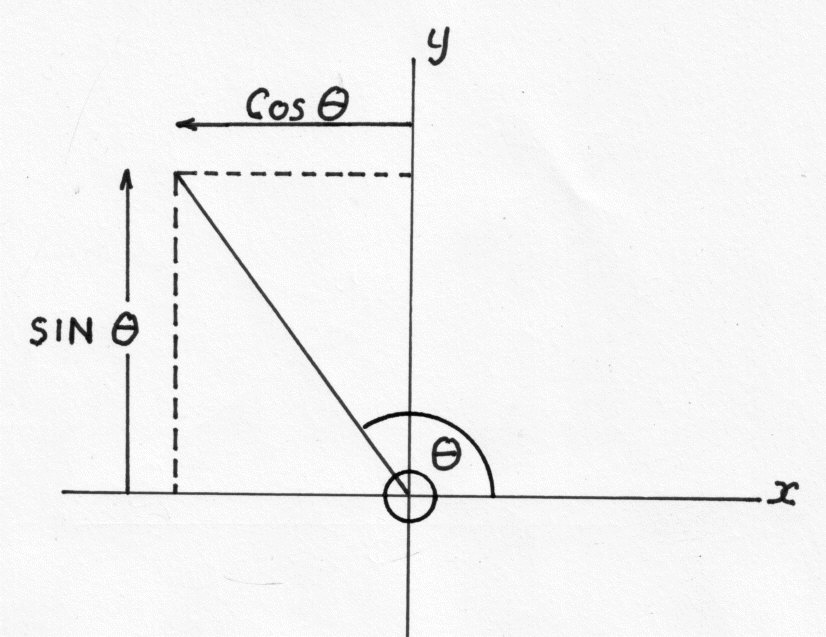
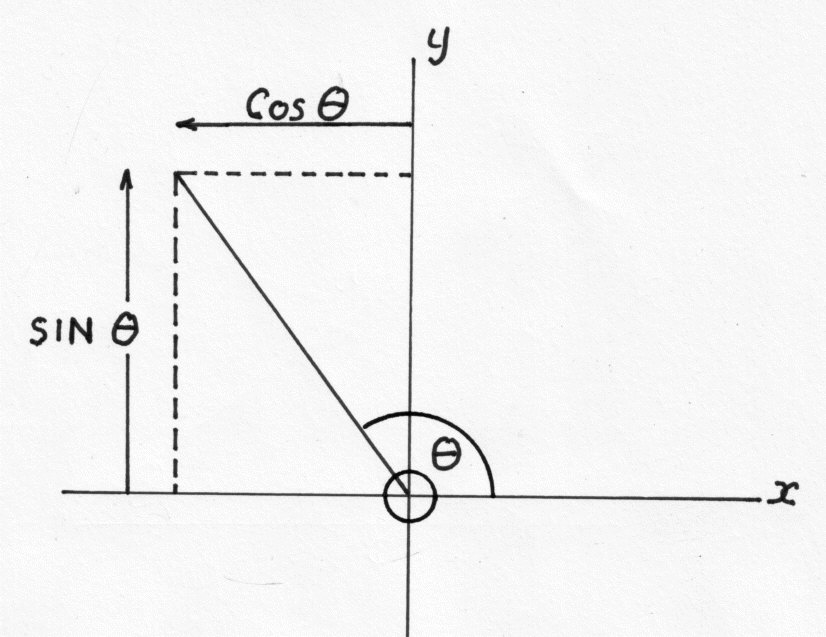
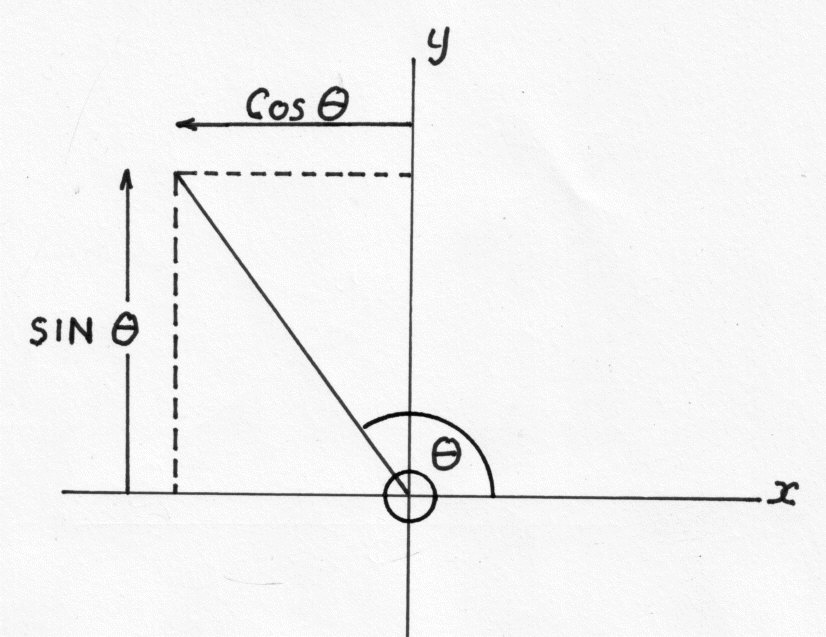
The Pythagorean identity in trigonometry is sin²(?) + cos²(?) = 1, where ? represents an angle in a right triangle. This identity is used to relate the trigonometric functions sine and cosine within a right triangle, specifically showing their relationship to the hypotenuse. By using the Pythagorean identity, trigonometric calculations and proofs can be simplified and relationships between sine and cosine can be better understood in various trigonometric problems.

How can the co-function identities be used to simplify trigonometric expressions?

Co-function identities can be used to simplify trigonometric expressions by replacing one trigonometric function with its co-function counterpart. This can help to convert trigonometric expressions involving sine, cosine, tangent, secant, cosecant, or cotangent functions to expressions involving complementary functions, leading to simpler calculations and easier identification of relationships between different trigonometric functions. By using co-function identities, trigonometric expressions can be transformed into equivalent forms that are easier to work with and manipulate algebraically.

Explain the double angle identities and give an example of how they can be used.

The double angle identities in trigonometry express trigonometric functions of twice an angle in terms of the trigonometric functions of the angle itself. For example, sin(2?) = 2sin?cos? and cos(2?) = cos^2(?) - sin^2(?). These identities are useful for simplifying trigonometric expressions, solving trigonometric equations, and proving trigonometric identities. For instance, if we have an expression involving sin(60°), we can use the double angle identity sin(2?) = 2sin?cos? with ? = 30° to simplify it into sin(60°) = 2sin(30°)cos(30°) = 2(1/2)(?3/2) = ?3/2.

How are the sum and difference of angles identities helpful in solving trigonometric equations?

The sum and difference of angles identities are helpful in solving trigonometric equations because they allow us to rewrite trigonometric expressions and equations in a simplified form that is easier to work with. By using these identities, we can express complex trigonometric functions in terms of simpler trigonometric functions, making it easier to manipulate and solve the equations. This simplification process can help us identify relationships between angles and trigonometric ratios, ultimately leading to a more systematic and efficient approach to solving trigonometric equations.

What are the reciprocal identities and why are they important in trigonometry?

The reciprocal identities in trigonometry are sine equals reciprocal cosecant, cosine equals reciprocal secant, and tangent equals reciprocal cotangent. These identities are crucial in trigonometry because they allow us to easily switch between trigonometric functions by taking reciprocals, simplifying calculations and expressions. They provide an efficient way to analyze trigonometric functions and relationships between angles, making them important tools in solving various trigonometric problems.

Describe the power-reducing identities and provide an example of their usage.

The power-reducing identities are trigonometric identities that express higher powers of sine and cosine functions in terms of lower powers. One such identity is the double angle identity: \( \sin^2(x) = \frac{1 - \cos(2x)}{2} \). This identity allows us to express \( \sin^2(x) \) in terms of \( \cos(2x) \), which is a simpler expression and can be more easily manipulated in trigonometric equations and calculations.

How does the quotient identity relate to other trigonometric functions?

The quotient identity in trigonometry, which states that tangent is equal to sine divided by cosine, is related to the other trigonometric functions through their interdependencies and their definitions in terms of each other. For example, the tangent function can be expressed in terms of sine and cosine, and similarly, the other trigonometric functions such as secant, cosecant, and cotangent can be derived from the basic sine and cosine functions using the quotient identity and other trigonometric identities. This shows the close relationship and interconnectedness between the various trigonometric functions in the unit circle and how they can be expressed in terms of one another.

Explain the periodicity identities and discuss their significance in trigonometric functions.

Periodicity identities in trigonometry refer to the properties of trigonometric functions that repeat their values at regular intervals. The main periodicity identities are for sine and cosine functions, where sin(x + 2?) = sin(x) and cos(x + 2?) = cos(x). These identities signify that the trigonometric functions have a repeating pattern after every 2? radians, which is the period of these functions. Understanding periodicity identities helps in simplifying trigonometric expressions and equations, as well as in analyzing and graphing trigonometric functions accurately. They are fundamental in trigonometry and play a crucial role in various mathematical and scientific applications.

What is the purpose of the even and odd identities in trigonometry?

The purpose of the even and odd trigonometric identities is to simplify trigonometric functions by expressing them in terms of simpler functions. Even identities relate the trigonometric functions to their corresponding functions with even symmetry (e.g., cosine is even, so cos(-x) = cos(x)), while odd identities relate them to their corresponding functions with odd symmetry (e.g., sine is odd, so sin(-x) = -sin(x)). This simplification helps in integrating functions, proving identities, and solving trigonometric equations more easily.