Trig Equations Worksheet

Trig equations can often be tricky to solve, requiring a solid understanding of angles, functions, and identities. For students looking to sharpen their skills in this area, a trig equations worksheet can serve as an invaluable tool. These worksheets aim to provide practice problems that cover various topics like solving equations involving sine, cosine, and tangent functions. By working through these exercises, students can effectively build their confidence and proficiency in solving trigonometric equations.

  Blank Graph Paper Worksheet

---

  Moves Dance Math-Beautiful

---

  Angle of Elevation and Depression Worksheet

---

  2nd Grade Math Worksheets

---

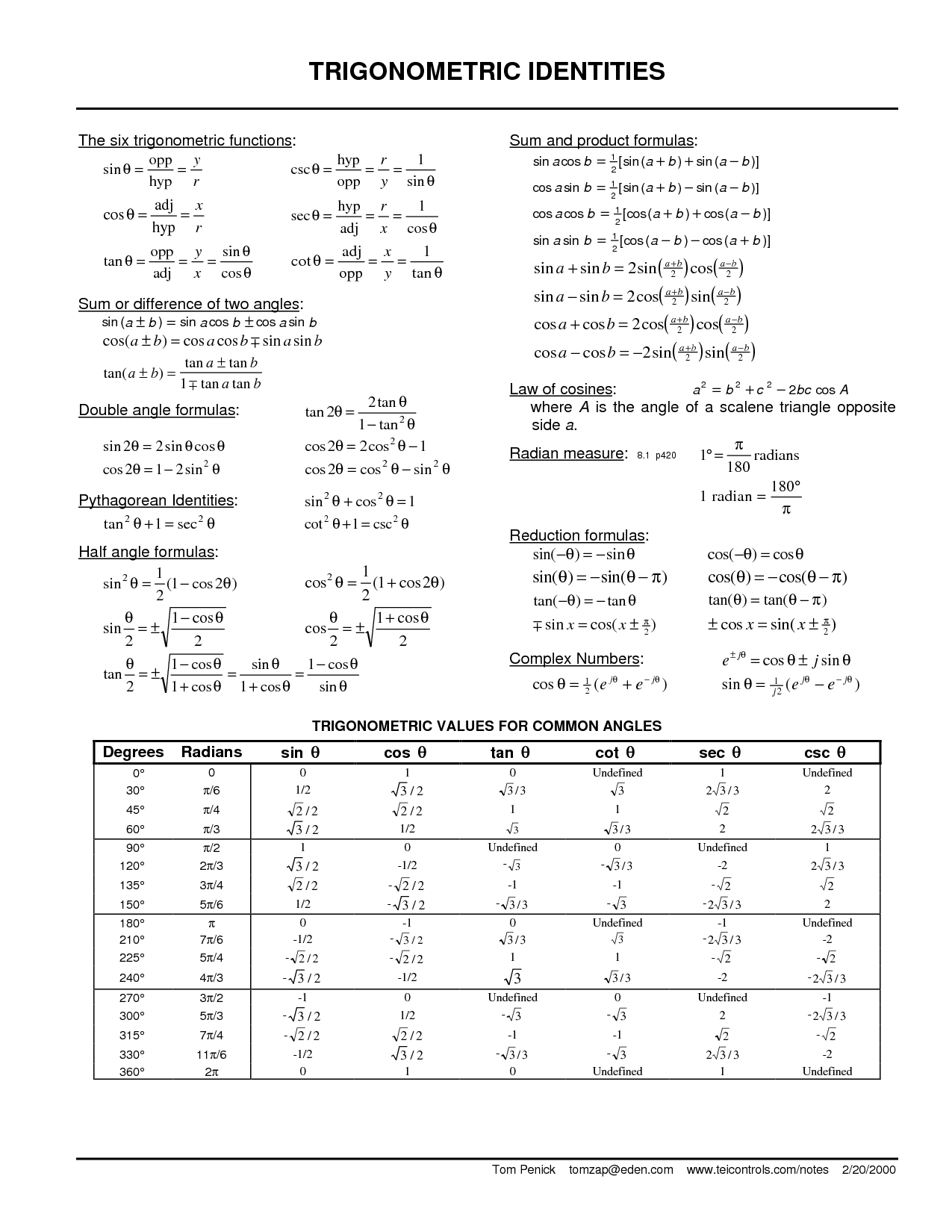
  Trig Identities Formula Sheet

---

  Quadrant Graph Trig Functions

---

  Accelerated Math Test Equations Circle

---

  Accelerated Math Test Equations Circle

---

  Teacher Answer Key

---

  Teacher Answer Key

---

  Teacher Answer Key

---

What is a trigonometric equation?

A trigonometric equation is an equation that involves trigonometric functions such as sine, cosine, tangent, secant, cosecant, or cotangent. These equations typically involve finding solutions for unknown angles or variables within the trigonometric functions. Trigonometric equations are commonly used in fields such as mathematics, physics, engineering, and astronomy to describe various phenomena or relationships involving angles and distances.

How can we solve basic trigonometric equations?

To solve basic trigonometric equations, identify the trigonometric function involved (sine, cosine, tangent, etc.) and isolate it on one side of the equation. Use inverse trigonometric functions to solve for the unknown angles. Remember to consider the domain restrictions and general solutions (adding multiples of 2? for periodic functions) when solving trigonometric equations. Brushing up on trigonometric identities and properties can also be helpful in simplifying and solving these equations efficiently. Practice and familiarity with the trigonometric functions will help improve your problem-solving skills in this area.

What is the fundamental principle for solving trigonometric equations?

The fundamental principle for solving trigonometric equations is to isolate the trigonometric function on one side of the equation and then apply inverse trigonometric functions or trigonometric identities to simplify and solve for the unknown variable. This involves using properties of trigonometric functions, such as the periodicity and symmetry of trigonometric functions, to manipulate the equation until a solution is obtained.

What are inverse trigonometric functions used for?

Inverse trigonometric functions are used to determine the angle that corresponds to a given trigonometric ratio. They are commonly used in various mathematical and scientific fields, such as calculating angles in navigational problems, analyzing waves and oscillations, and solving problems in physics and engineering. Additionally, they are useful in solving equations involving trigonometric functions and in graphical representations of trigonometric functions.

Can trigonometric equations have multiple solutions?

Yes, trigonometric equations can have multiple solutions. This is because trigonometric functions are periodic, meaning they repeat themselves at regular intervals. When solving trigonometric equations, there are often multiple angles within the given interval that satisfy the equation. These multiple solutions can be accounted for by adding integer multiples of the period of the trigonometric function to the initial solution.

What are identities and how are they related to trigonometric equations?

Identities in trigonometry refer to equations that are true for all values of the variables involved. These identities are helpful in simplifying and solving trigonometric equations because they provide relationships between trigonometric functions, allowing us to manipulate expressions and equations to make them easier to work with. By using identities such as the Pythagorean identities or angle sum and difference identities, we can transform complex trigonometric equations into simpler forms that are easier to solve and understand.

How can we use the unit circle to solve trigonometric equations?

To solve trigonometric equations using the unit circle, first rewrite the equation in terms of sine and cosine functions. Then, find the values of the angles that satisfy the equation by identifying the points on the unit circle where the sine or cosine of the angle matches the values in the equation. This allows you to determine the solutions to the trigonometric equation by understanding the relationship between angles, sine, cosine, and the unit circle.

Are there any special strategies for solving trigonometric equations?

Yes, there are several strategies for solving trigonometric equations, including using trigonometric identities, factoring, applying the unit circle, using the periodicity of trigonometric functions, and employing inverse trigonometric functions. It's crucial to simplify the equation as much as possible and identify any patterns or relationships that can help in finding solutions effectively. Experimenting with different methods and being familiar with trigonometric properties can aid in solving these types of equations more efficiently.

How can we use graphs to solve trigonometric equations?

Graphs can be used to solve trigonometric equations by plotting the trigonometric functions involved in the equation and finding the points of intersection between the graphs of the functions. These points of intersection represent the solutions to the equation. By analyzing the graph, we can visually determine the values of the angles that satisfy the trigonometric equation, making it easier to find the solutions.

What are real-world applications of trigonometric equations?

Trigonometric equations have numerous real-world applications such as in architecture for designing buildings and bridges, in engineering for analyzing mechanical systems and electrical circuits, in physics for modeling wave behavior and vibrations, in navigation for calculating distances and angles, in astronomy for tracking celestial objects, and in computer graphics for creating realistic animations and visual effects. Additionally, trigonometric equations are also used in fields like surveying, seismology, and music theory.