Triangle for Family Counseling Worksheets
Family counseling is a powerful tool that helps strengthen relationships and create stronger bonds within a family unit. But where do you find the right resources to facilitate this process? Look no further than our collection of triangle worksheets designed specifically for family counseling. These worksheets provide a dynamic and engaging way for families to explore their emotions, communication styles, and relationships, making them an excellent resource for therapists, counselors, and families seeking to improve their connection and understanding.
Table of Images 👆
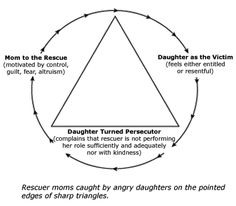
- Karpman Drama Triangle Diagram
- Printable Marriage Counseling Worksheets
- Pinterest Behavior Management Worksheets
- Pre-K Shapes Worksheets
- Clip Art Fact Family Triangles
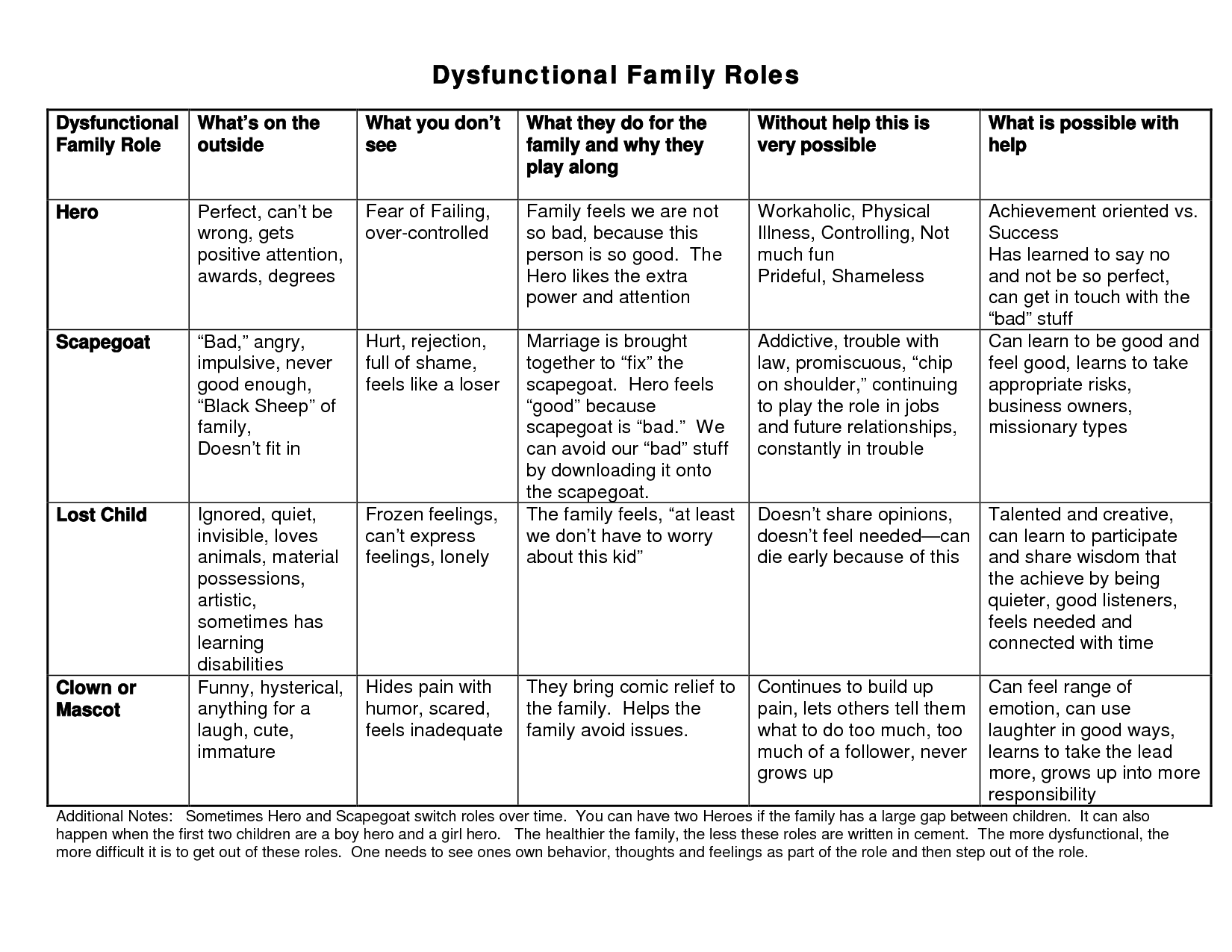
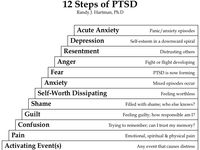
- Dysfunctional Family Roles Chart
- Cognitive Behavioral Therapy
- Dialectical Behavior Therapy Distress Tolerance
- Karpman Drama Triangle Diagram
- Humanistic-Existential Personality Theories and Worksheet
- Triangle Borderline Personality Disorder
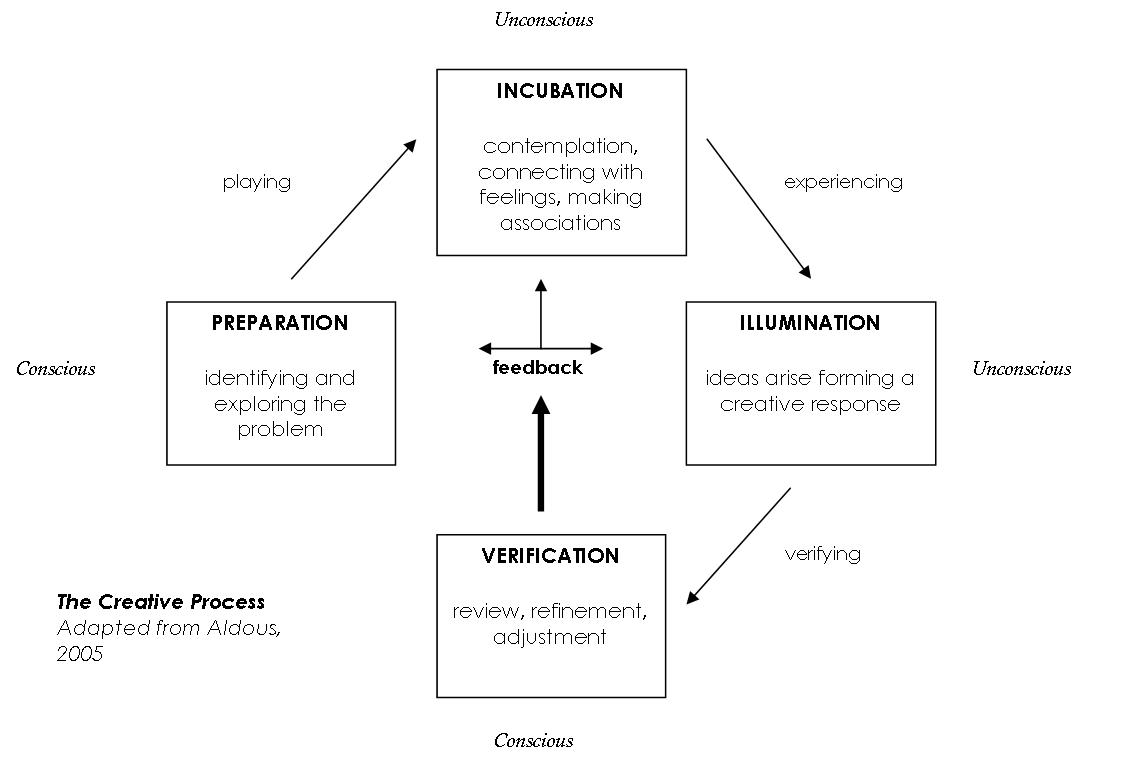
- Creative Art Therapy Process
- Criminal Thinking Errors Worksheet
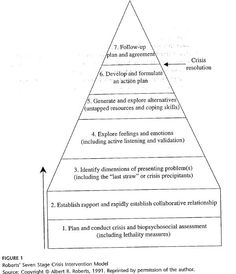
- 7 Stage Crisis Intervention Model
- Health Worksheets Middle School
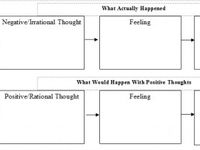
- Thoughts and Feelings Worksheets
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
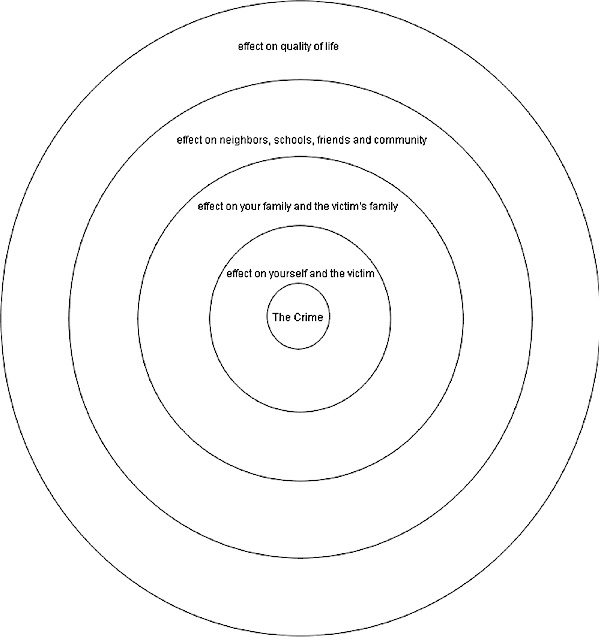
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What are the different types of triangles?
There are three main types of triangles based on their side lengths and angles: equilateral triangles have three equal sides and angles, isosceles triangles have two equal sides and angles, and scalene triangles have no equal sides or angles. Additionally, triangles can be categorized based on their angles as acute triangles (all angles are less than 90 degrees), obtuse triangles (one angle is greater than 90 degrees), and right triangles (one angle is exactly 90 degrees).
How can you determine the area of a triangle?
To determine the area of a triangle, you can use the formula: Area = 1/2 * base * height. Simply multiply the base of the triangle by the height of the triangle, and then divide the product by 2 to get the area. Make sure to measure the base and height accurately for an precise calculation of the area of the triangle.
What is the Pythagorean theorem and how is it used in triangles?
The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. Mathematically, it is expressed as a² + b² = c², where 'c' is the length of the hypotenuse, and 'a' and 'b' are the lengths of the other two sides of the triangle. This theorem is widely used in geometry to calculate the unknown side lengths of a right triangle, or to determine if a triangle is a right triangle. It is a fundamental principle in mathematics and has various applications in fields like engineering, physics, and architecture.
What is the difference between an acute, obtuse, and right triangle?
The main difference between an acute, obtuse, and right triangle lies in the angles formed by their sides. In an acute triangle, all three angles are less than 90 degrees. In an obtuse triangle, one angle is greater than 90 degrees. In a right triangle, one angle is exactly 90 degrees. These distinctions help classify triangles based on the measure of their angles and can impact various properties and relationships within the triangle.
How can you find the perimeter of a triangle?
To find the perimeter of a triangle, add together the lengths of all three sides of the triangle. Summing up the lengths of these three sides will give you the total perimeter of the triangle.
What is the relationship between the angles and sides in an equilateral triangle?
In an equilateral triangle, all three angles are equal and measure 60 degrees, while all three sides are also equal in length. This means that the relationship between the angles and sides in an equilateral triangle is that they are all congruent to each other.
How can you find the missing angle in a triangle?
To find the missing angle in a triangle, you can use the fact that the sum of the three angles in a triangle is always 180 degrees. So, to find the missing angle, subtract the measurements of the two known angles from 180 degrees. This will give you the measurement of the missing angle in the triangle.
What is the Law of Sines and how does it apply to triangles?
The Law of Sines states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is constant for all three sides of the triangle. This law is used to solve triangles when given certain angle and side measurements, allowing us to find missing angles or sides. It is particularly useful in non-right triangles, where traditional trigonometric functions may not be directly applicable.
How does the concept of similarity relate to triangles?
In triangles, the concept of similarity refers to two or more triangles that have the same shape but possibly different sizes. When two triangles are similar, their corresponding angles are congruent, and their corresponding sides are in proportion to each other. This means that you can determine the lengths of unknown sides in similar triangles by setting up proportions with the corresponding sides of the triangles. Similarity is a key concept in geometry that helps us analyze and solve problems involving triangles.
How can you use trigonometric functions (such as sine, cosine, and tangent) to solve triangle problems?
Trigonometric functions, such as sine, cosine, and tangent, can be used in solving triangle problems through trigonometric ratios. For example, in a right-angled triangle, the sine of an angle is calculated as the ratio of the length of the side opposite to that angle to the length of the hypotenuse. Similarly, cosine is the ratio of the length of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side. These ratios can help find missing side lengths or angles in a triangle when the other values are known, making trigonometric functions essential tools for solving various triangle problems.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.


























Comments