Translation Reflection and Rotation Worksheets

Are you seeking engaging and educational ways to support your students' understanding of translation, reflection, and rotation? Look no further! Our collection of worksheets is designed to help students grasp the concepts of these mathematical transformations. Whether you are a teacher looking for additional resources or a parent wanting to provide extra practice, our worksheets offer an interactive and visual approach to exploring these topics.

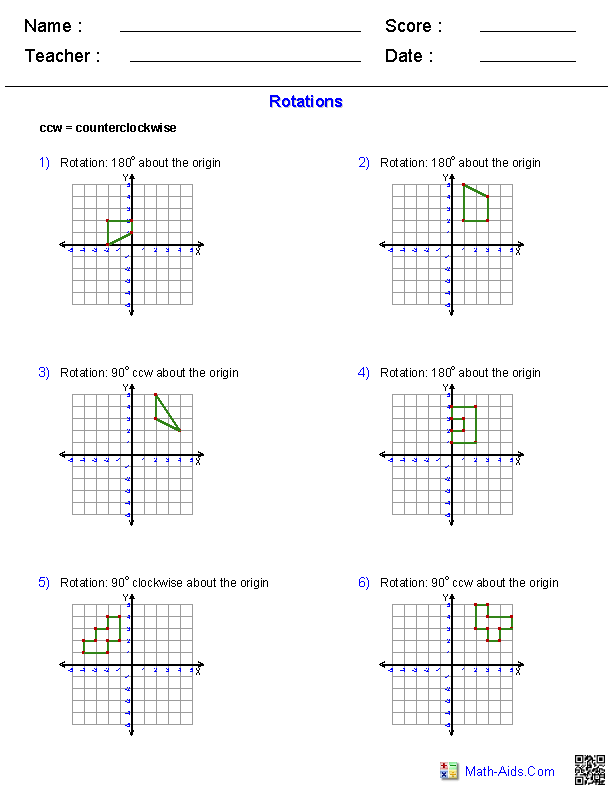
  Geometry Rotations Worksheet

---

  Common Core 8 Grade Translations Worksheet

---

  Rotational Symmetry Worksheets

---

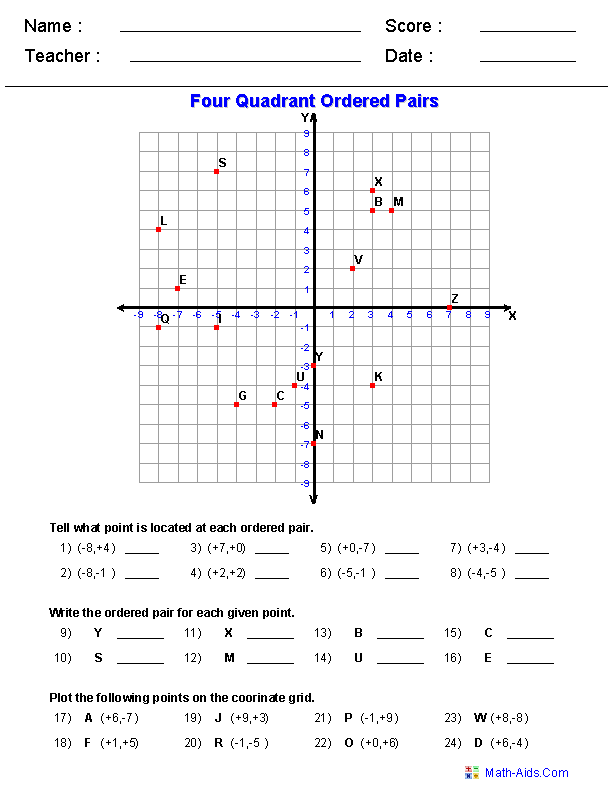
  Graphing Coordinate Plane Worksheets 6th Grade

---

  Cups Pints Quarts Gallons

---

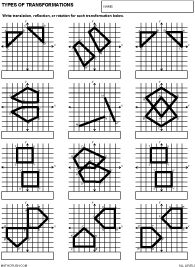
  Types of Math Transformation Worksheets

---

  Reflecting On Your Life

---

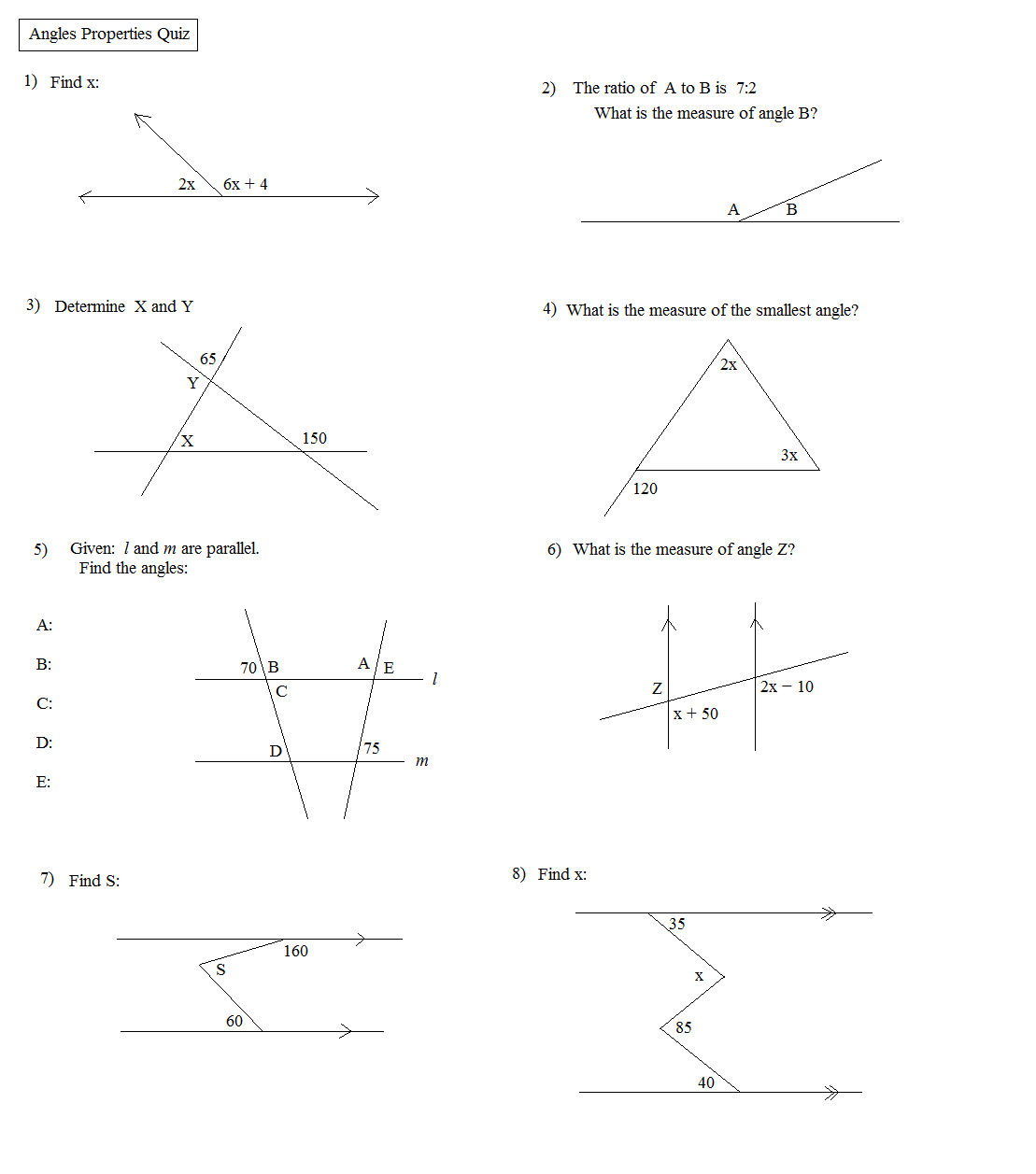
  Angle Properties Worksheet

---

  Solving Algebra Equations Worksheets

---

  Exponents Worksheets with Answers

---

What is translation in mathematics?

Translation in mathematics refers to the transformation of an object by moving it from one location to another without changing its size, shape, or orientation. This is often achieved by shifting all points of the object in the same direction and by the same distance. Translation is a fundamental concept in geometry and is commonly used to study the properties and relationships of geometric figures.

How is a figure reflected over a line?

To reflect a figure over a line, you need to mirror the figure across the line. Each point on the original figure is reflected across the line by creating a perpendicular line connecting the point to the line of reflection. The reflected point is then located the same distance on the opposite side of the line of reflection. Repeat this process for every point on the figure to obtain the reflected figure.

What is the rotational symmetry of a shape?

Rotational symmetry of a shape is when a shape can be rotated by a certain angle (typically less than 360 degrees) and still look exactly the same as its original orientation. This means that the shape has multiple positions where it aligns perfectly with its original position during a partial rotation. The number of positions in which the shape looks the same after a rotation is equal to the number of lines of symmetry it possesses.

How do you determine the image of a shape after translation?

To determine the image of a shape after translation, you need to move each point of the original shape by the same distance and direction. The rule of translation involves shifting the shape horizontally and vertically based on a given vector. By applying this rule to all points of the shape, you can calculate the new position of each point to find the image after translation.

What is the difference between a translation and a reflection?

In mathematics, a translation involves moving an object from one location to another in a straight line without changing its orientation. On the other hand, a reflection involves flipping an object over a line, such as a mirror line, resulting in a mirror image of the original object. Therefore, the main difference between a translation and a reflection is that a translation involves shifting an object while keeping its orientation the same, while a reflection involves flipping an object over a line.

What are some real-life examples of translation?

Some real-life examples of translation include translating books and articles, interpreting conversations between people speaking different languages, localizing websites and software for different markets, and providing subtitles for films and TV shows in different languages. Translation plays a crucial role in fostering communication and understanding across cultures and languages in various fields such as business, diplomacy, literature, and entertainment.

How do you describe a reflection over the x-axis?

A reflection over the x-axis involves flipping a shape or object across the x-axis. This means that each point on the object is moved to its mirror image across the x-axis while keeping the same distance from the x-axis. The y-coordinates of the points are negated during this transformation.

In what situations would you use rotation in mathematics?

Rotation in mathematics is commonly used in geometry to describe the movement of shapes around a fixed point. It is also frequently employed in linear algebra to transform vectors and matrices. Rotations can be used in computer graphics to create animations and 3D effects, as well as in physics to describe the orientation of objects in space. Overall, rotations are utilized in various mathematical applications to analyze and manipulate objects in different dimensions.

How do you determine the image of a shape after rotation?

To determine the image of a shape after rotation, you can follow a few steps. First, identify the center of rotation and the angle of rotation. Then, analyze how each point of the shape will move following the rotation. Apply the rotation transformation equations to calculate the new coordinates of each point after rotation. Finally, plot the new points to visualize the image of the shape after rotation. Remember that the angle of rotation determines the direction and extent of the rotation, whether it is clockwise or counterclockwise.

What are some real-life applications of rotation?

Rotations have various real-life applications in fields such as engineering, robotics, animation, and physics. Examples include designing mechanical parts like gears and turbines that rotate to perform specific functions, controlling the movement of robotic arms and drones for precise operation, animating characters and objects in video games and movies to simulate realistic movements, and understanding the rotational motion of planets and stars in astrophysics. Rotations are also crucial in sports like gymnastics, figure skating, and diving, where athletes perform rotational movements to execute complex maneuvers and stunts.