Surface Area Rectangular Prism Volume Worksheet

Finding the surface area and volume of a rectangular prism can be a challenging task for many students. If you are a math teacher or a student struggling with these concepts, you've come to the right place. In this blog post, we will explore worksheets that focus on practicing and mastering the calculations of surface area and volume of rectangular prisms. These worksheets are designed to make learning fun and engaging, providing ample opportunities to strengthen your understanding of these key mathematical concepts.

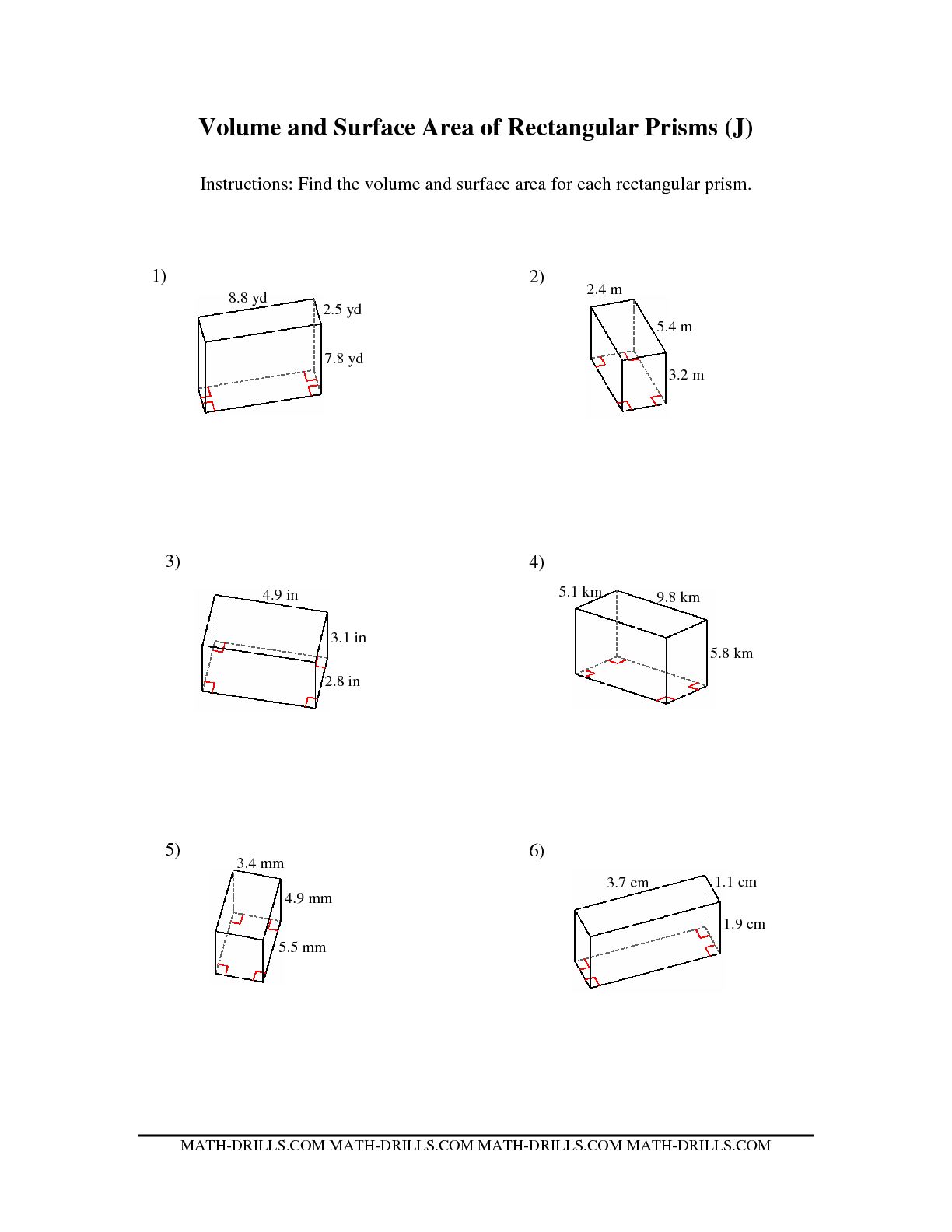
  Surface Area Rectangular Prism Volume

---

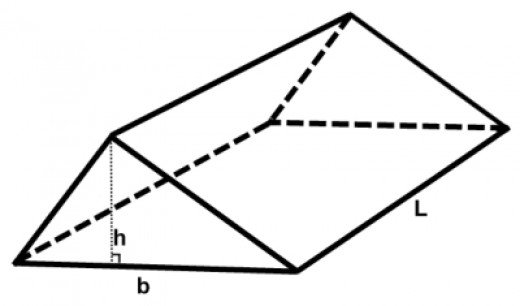
  Triangular Prism Surface Area and Volume Worksheets

---

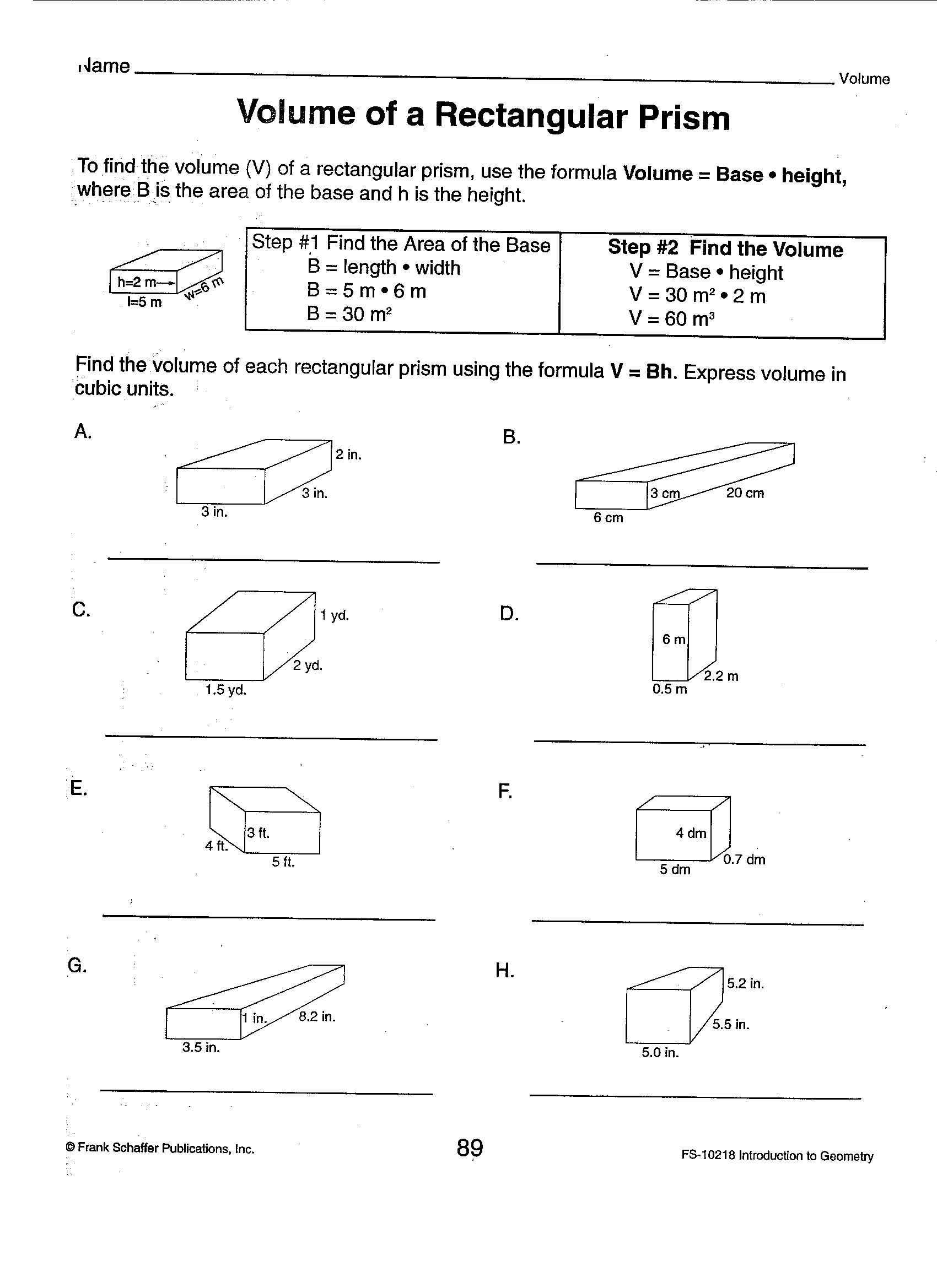
  Volume Rectangular Prisms with Cubes Worksheet

---

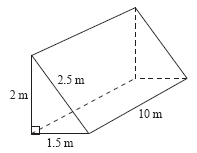
  Surface Area Triangular Prism

---

  Volume Worksheets 5th Grade

---

  8th Grade Math Practice Worksheets

---

  Triangular Prism

---

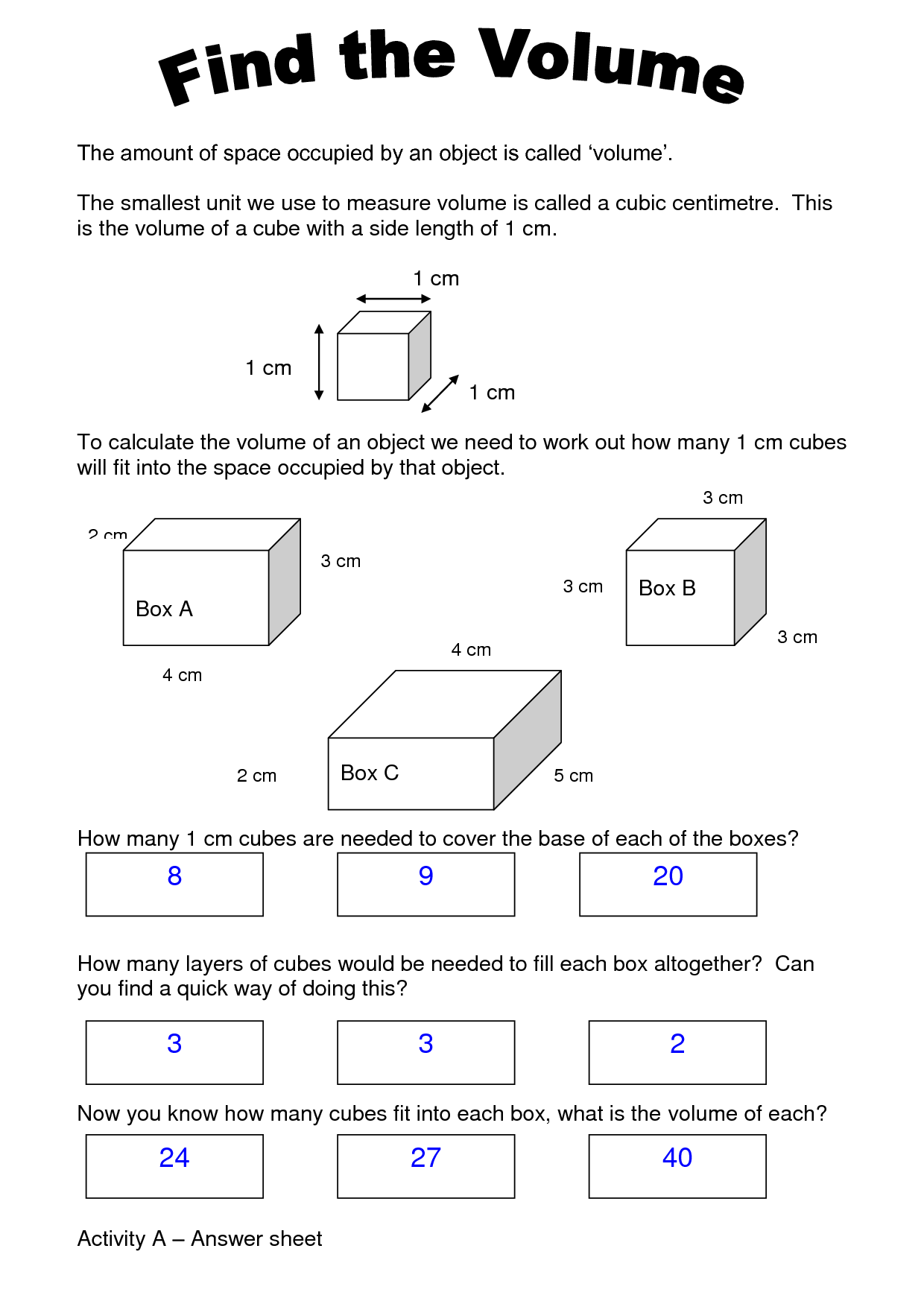
  Volume Counting Cubes

---

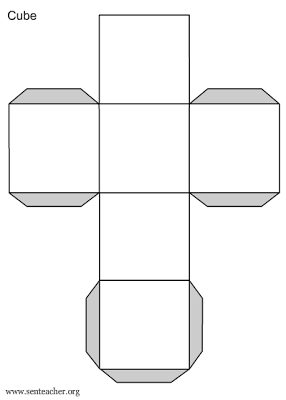
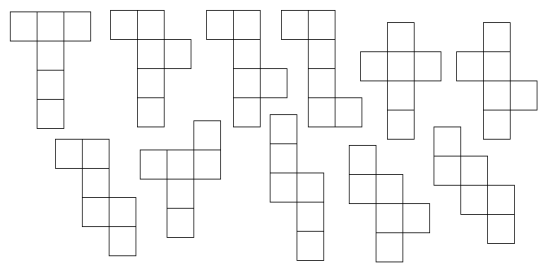
  3D Shape Nets to Print

---

  Surface Area Triangular Prism

---

  A of a Rectangular Prism and Cube Nets

---

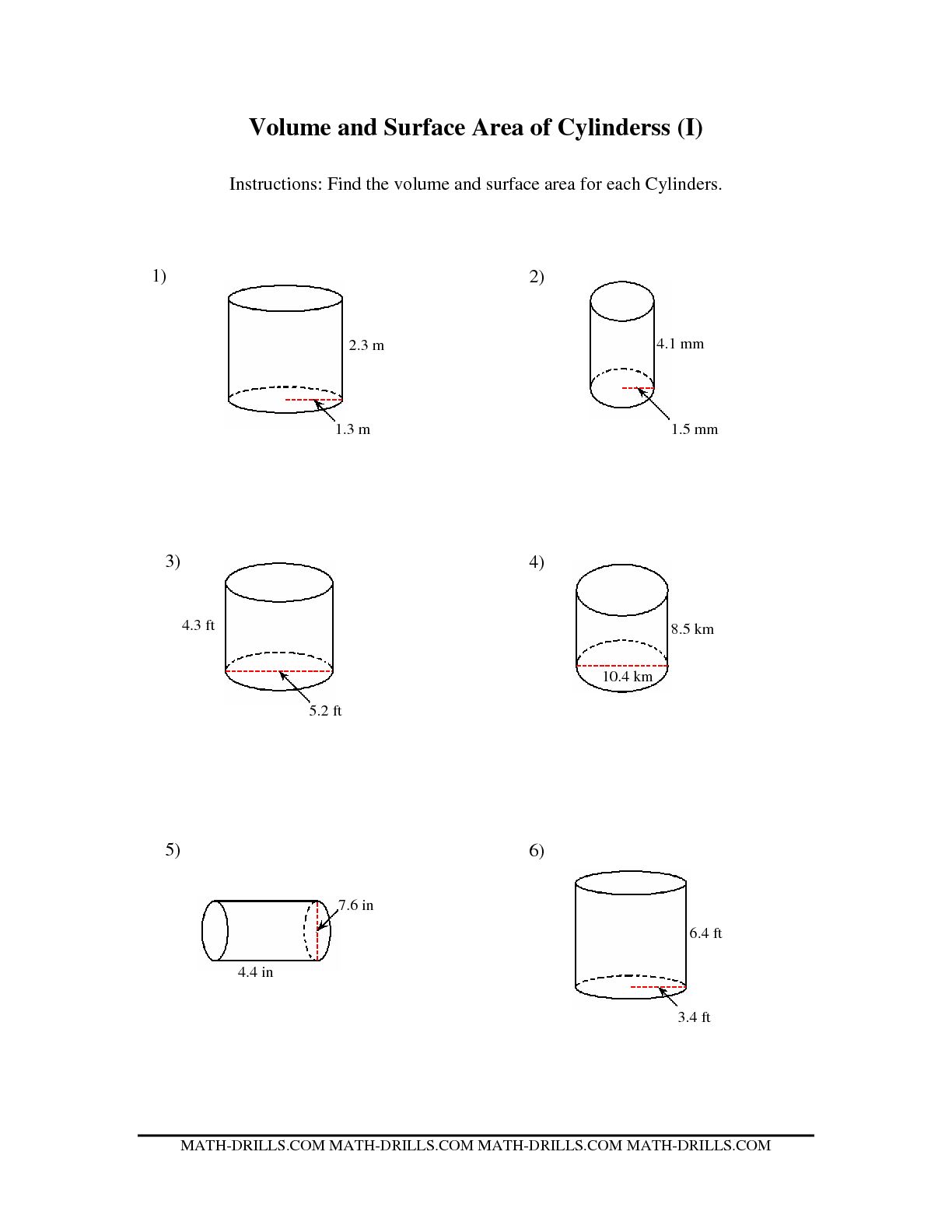
  Surface Area Volume Cylinder Worksheet

---

  Surface Area and Volume of Cones Worksheets

---

  Surface Area and Volume of Cones Worksheets

---

What is the formula for finding the surface area of a rectangular prism?

The formula for finding the surface area of a rectangular prism is 2(lw + lh + wh), where l is the length, w is the width, and h is the height of the prism.

Calculate the surface area of a rectangular prism with dimensions 5cm, 6cm, and 7cm.

To calculate the surface area of a rectangular prism, you can use the formula 2lw + 2lh + 2wh, where l, w, and h are the length, width, and height of the prism, respectively. In this case, the dimensions are 5cm, 6cm, and 7cm. Plugging these values into the formula, we get 2(5*6) + 2(5*7) + 2(6*7) = 60 + 70 + 84 = 214 square cm. Thus, the surface area of the rectangular prism is 214 square centimeters.

How many faces does a rectangular prism have?

A rectangular prism has six faces: top, bottom, front, back, and two side faces.

What is the formula for finding the volume of a rectangular prism?

The formula for finding the volume of a rectangular prism is V = l × w × h, where V represents volume, l is the length, w is the width, and h is the height of the prism.

Calculate the volume of a rectangular prism with dimensions 10m, 8m, and 6m.

To calculate the volume of a rectangular prism, you multiply the three dimensions together. Therefore, the volume of a rectangular prism with dimensions 10m, 8m, and 6m is 10m * 8m * 6m = 480 cubic meters.

What does the surface area of a rectangular prism represent?

The surface area of a rectangular prism represents the total area of all the faces of the prism, including the top, bottom, front, back, and sides. It is a measure of the amount of space that the outer part of the prism covers and helps in determining how much material is needed to cover or paint the prism.

What units are typically used to measure surface area?

Surface area is typically measured in square units, such as square meters (m²) or square feet (ft²), depending on the system of measurement being used.

How is the surface area of a rectangular prism different from its volume?

The surface area of a rectangular prism refers to the total area that encompasses all of its surfaces, which includes the area of the six faces. In contrast, the volume of a rectangular prism refers to the amount of space that is enclosed within the prism. While surface area is measured in square units (e.g., square meters), volume is measured in cubic units (e.g., cubic meters). Thus, the surface area represents the total amount of material needed to cover the exterior of the prism, while the volume represents the space contained within the prism.

What is the relationship between the length, width, and height of a rectangular prism and its volume?

The volume of a rectangular prism is directly related to its length, width, and height. The formula to calculate the volume of a rectangular prism is Volume = Length x Width x Height. This means that as the length, width, or height of the rectangular prism increases, its volume will also increase proportionally. Conversely, if the length, width, or height decreases, the volume will also decrease. This shows that the dimensions of a rectangular prism have a direct impact on its volume.

Why is it important to understand the concepts of surface area and volume in relation to rectangular prisms?

It is important to understand the concepts of surface area and volume in relation to rectangular prisms because these measurements provide crucial information about the shape and size of the prism. Surface area helps us determine the amount of material needed to cover the prism, while volume tells us how much space the prism occupies. These calculations are essential in fields such as architecture, engineering, and manufacturing to ensure accurate designs, efficient material usage, and proper functionality of structures or objects. Understanding surface area and volume also improves our spatial reasoning skills and ability to solve real-world problems involving rectangular prisms.