Solving Two Variable Equations Worksheets

If you're seeking a reliable resource to help your students master solving two variable equations, you've come to the right place. Worksheets are an effective way to engage and test their understanding of this mathematical concept. With a clear focus on the entity and subject, these worksheets provide concise and structured practice opportunities that will enhance their problem-solving skills.

  One Step Equations Worksheets

---

  Variable Expressions and Equations Worksheets

---

  Evaluating Algebra Expressions Worksheets

---

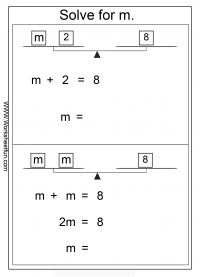
  Literal Equations Worksheet with Answers

---

  Algebra Linear Equations Worksheets with Answers

---

  Algebra Equations Word Problems Worksheets

---

  4th Grade Math Word Problems

---

  Solve Algebra Equation Worksheet

---

  4th Grade Multiplication Comparison Problems

---

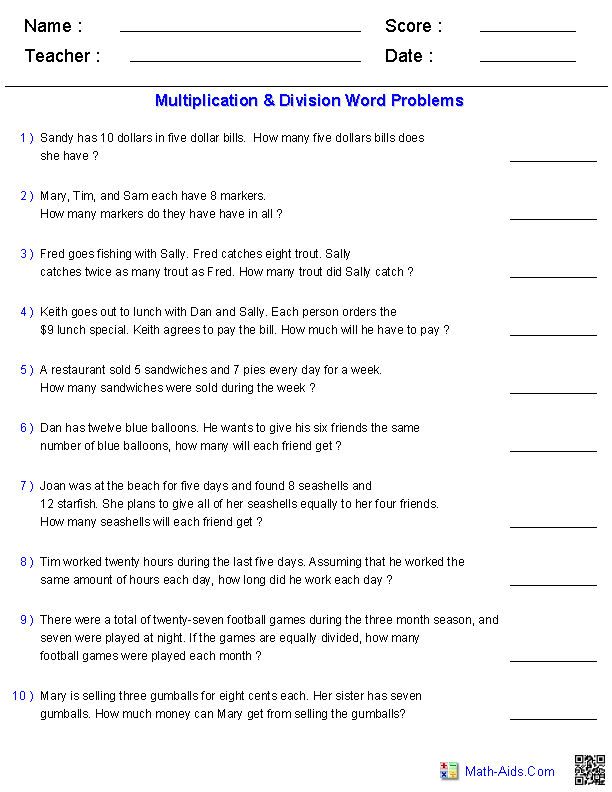
  Multiplication and Division Word Problems

---

  Equations with Distributive Property

---

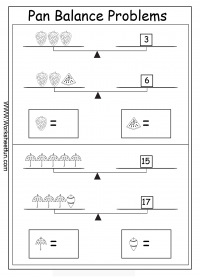
  Pan Balance Problems 5th Grade Worksheets

---

  Lambda Calculus Examples

---

  Lambda Calculus Examples

---

  Lambda Calculus Examples

---

  Lambda Calculus Examples

---

What is the purpose of solving two variable equations?

The purpose of solving two variable equations is to find the values of the variables that satisfy both equations simultaneously. This allows us to determine the intersection point of two lines or the solution to a system of equations, helping us understand the relationship between the two variables and make predictions or calculations based on that relationship.

What are the steps involved in solving two variable equations?

To solve two variable equations, first identify the two equations. Choose a method to solve the equations such as substitution, elimination, or graphing. Use the chosen method to solve for one variable in terms of the other in one of the equations. Substitute this value into the other equation to find the value of the second variable. Verify the solution by substituting the values back into the original equations and check if they hold true.

How can we determine if a given point is a solution to a two variable equation?

To determine if a given point is a solution to a two variable equation, substitute the values of the variables in the point into the equation and simplify. If the resulting expression is true, then the point is a solution to the equation. If the expression is false, then the point is not a solution to the equation.

What is the difference between consistent, inconsistent, and dependent systems of equations?

In a consistent system of equations, there is at least one solution that satisfies all the equations simultaneously. In an inconsistent system of equations, there are no solutions, meaning the equations contradict each other. A dependent system of equations has infinitely many solutions, where the equations are essentially the same or can be reduced to each other through algebraic manipulation.

How can we represent two variable equations graphically?

Two-variable equations can be graphically represented as lines on a coordinate plane. To graph an equation like y = mx + b, where m is the slope and b is the y-intercept, you can plot the y-intercept on the y-axis and use the slope to find additional points on the line. For equations in the form of Ax + By = C, you can rearrange to solve for y and graphing the resulting linear equation. The point where the two lines intersect represents a solution to the system of equations.

Can simultaneous equations have more than one solution?

Yes, simultaneous equations can have more than one solution. Whether a system of simultaneous equations has one solution, no solution, or infinite solutions depends on the specific equations and their relationship to each other. In cases where the equations represent parallel lines or overlapping lines, there can be multiple solutions that satisfy all equations simultaneously.

How can substitution be used to solve a system of two variable equations?

In solving a system of two variable equations using substitution, one of the equations is solved for one variable, and then that expression is substituted into the other equation. This allows for the system to be reduced to a single variable equation, which can then be easily solved to find the values of the variables. By substituting the expression for one variable from one equation into the other equation, a new equation can be formed with only one variable, making it possible to solve the system and find the values of the variables.

What is the role of elimination in solving two variable equations?

The role of elimination in solving two variable equations is to eliminate one of the variables by adding or subtracting the equations in a way that one variable gets canceled out, allowing us to solve for the other variable. This method helps simplify the equations and make it easier to find the solution where the two equations intersect, representing the values of the variables that satisfy both equations simultaneously.

How do we solve word problems involving two variable equations?

To solve word problems involving two variable equations, you first need to translate the information given in the problem into mathematical equations. Assign variables to the unknown quantities, write equations that represent the given relationships, and then solve the system of equations using methods like substitution or elimination. Once you have found the values of the variables that satisfy both equations, you can interpret the solutions in the context of the original word problem to arrive at the final answer. Practice and patience are key to mastering this skill.

Are there any strategies or shortcuts that can be used when solving two variable equations?

One strategy or shortcut that can be used when solving two variable equations is substitution, where one variable is isolated in one equation and then substituted into the other equation. This can help simplify the equations and make it easier to solve for the remaining variable. Another common strategy is to eliminate one variable by adding or subtracting the equations to create a new equation with only one variable, making it simpler to solve. Additionally, graphing the equations can help visualize where they intersect, which is the solution to the system of equations.