Solving Quadratic Equations with Square Roots Worksheet
Quadratic equations can be a tricky concept to grasp, especially when it comes to solving them using square roots. If you're a student struggling with this particular topic or a teacher searching for a resource to help your students, you're in luck. This blog post introduces a comprehensive worksheet designed to reinforce understanding of solving quadratic equations with square roots.
Table of Images 👆
- Solving Square Root Equations Worksheet
- Quadratic Equation Worksheets with Answers
- Solving Exponential Equations
- Quadratic Equation with No Solution Example
- Kuta Software Infinite Algebra 1 Answers Key
- Quadratic Functions Worksheet
- Cobblestone Street Manhattan
- Square Shape Worksheet
- Grade Math Worksheets for Elementary
- Dividing Polynomials Worksheet
- Dividing Polynomials Worksheet
- Dividing Polynomials Worksheet
- Dividing Polynomials Worksheet
- Dividing Polynomials Worksheet
- Dividing Polynomials Worksheet
- Dividing Polynomials Worksheet
- Dividing Polynomials Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is a quadratic equation?
A quadratic equation is a second-degree polynomial equation that contains terms of the form ax^2 + bx + c, where a, b, and c are constants with a not equal to 0, and x is the variable. When graphed, a quadratic equation forms a parabolic curve, and it can have zero, one, or two real roots depending on the discriminant (b^2 - 4ac) of the equation.
When is a quadratic equation said to have real solutions?
A quadratic equation is said to have real solutions when the discriminant, which is the part of the quadratic formula underneath the square root (b^2 - 4ac), is greater than or equal to zero. This means that the equation has two distinct real roots or one real repeated root, representing points where the parabola defined by the quadratic equation intersects the x-axis.
What is the quadratic formula?
The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a, where a, b, and c are coefficients of a quadratic equation in the form ax^2 + bx + c = 0. This formula is used to find the solutions or roots of the quadratic equation.
How do you solve a quadratic equation using square roots?
To solve a quadratic equation using square roots, you first isolate the squared term on one side of the equation. Then you take the square root of both sides to eliminate the square term, remembering to include both the positive and negative square root to account for both possible solutions. Finally, you simplify the expression and solve for the variable to find the solutions to the quadratic equation.
What are the steps involved in solving a quadratic equation with square roots?
To solve a quadratic equation with square roots, you would first isolate the squared term on one side of the equation. Then you would square both sides to eliminate the square root. This will result in a standard quadratic equation that you can solve using methods like factoring, completing the square, or the quadratic formula. Once you find the solutions, remember to check them in the original equation to ensure they are valid.
Can a quadratic equation have more than two solutions?
No, a quadratic equation can have at most two solutions, whether real or complex. This is because a quadratic equation is a second-degree polynomial equation, which means it can be represented by a parabola that intersects the x-axis at most twice. If the quadratic equation has fewer than two real solutions, the remaining solution(s) will be complex conjugates.
How do you determine if a quadratic equation has no real solutions?
You can determine if a quadratic equation has no real solutions by looking at the discriminant, which is the part of the quadratic formula inside the square root (√) symbol. If the discriminant is negative, then the quadratic equation has no real solutions because it would involve taking the square root of a negative number, which is not a real number.
How can you check if your solution is correct for a quadratic equation?
To check if your solution is correct for a quadratic equation, you can substitute the values of the solutions back into the original equation and see if they satisfy it. If both solutions satisfy the equation when substituted, then your solution is correct. It's also a good practice to verify your answer by simplifying the equation and confirming that it equals zero.
What are some common mistakes to avoid when solving quadratic equations with square roots?
Some common mistakes to avoid when solving quadratic equations with square roots include not isolating the square root term before squaring both sides, forgetting to consider both the positive and negative square root solutions, neglecting to check for extraneous solutions that may arise from squaring both sides, and miscalculating the arithmetic involved in simplifying the equation. It is important to be attentive, methodical, and thorough in your approach to avoid falling into these traps when solving quadratic equations with square roots.
Can you give an example of a quadratic equation solved using square roots?
Sure, one example of a quadratic equation solved using square roots is x^2 - 4x + 4 = 0. To solve this equation, we can first identify the coefficients a, b, and c where a = 1, b = -4, and c = 4. Then, we can use the quadratic formula x = (-b ± √(b^2 - 4ac)) / 2a to find the roots. Substituting the values of a, b, and c into the formula gives x = (4 ± √((-4)^2 - 4*1*4)) / 2*1, which simplifies to x = (4 ± √(16 - 16)) / 2, then x = (4 ± √0) / 2, and finally x = 4 / 2, or x = 2. So, the solution to the quadratic equation x^2 - 4x + 4 = 0 is x = 2.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.







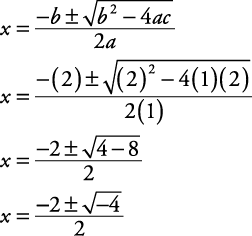

























Comments