Solving Matrices Worksheets
Matrices can often be a daunting topic for students, but with the right practice materials, mastering them becomes much more manageable. In order to help students grasp the concepts and techniques involved in solving matrices, we have curated a collection of worksheets that specifically focus on this area of mathematics. These worksheets provide a wide range of practice questions, allowing students to strengthen their skills in manipulating matrices and solving related problems.
Table of Images 👆
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the purpose of solving matrices?
The purpose of solving matrices is to efficiently manipulate and analyze complex systems of equations, helping to solve various problems in mathematics, physics, engineering, and many other fields. Matrices provide a structured way to represent and organize data, enabling us to perform operations such as addition, subtraction, multiplication, and inversion, which are crucial for solving linear systems, optimizing processes, and understanding the behavior of dynamic systems. Overall, solving matrices allows us to tackle sophisticated problems and gain valuable insights into the behavior of interconnected variables.
What are the steps involved in solving matrices?
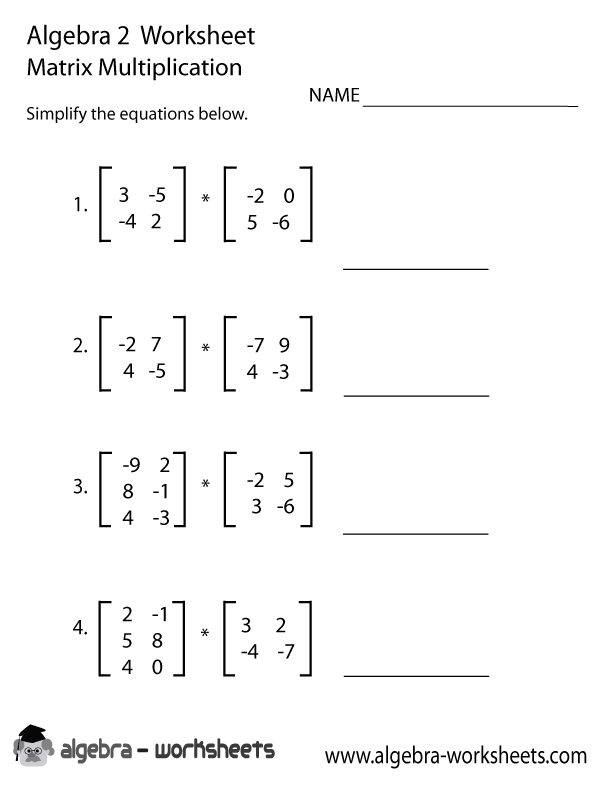
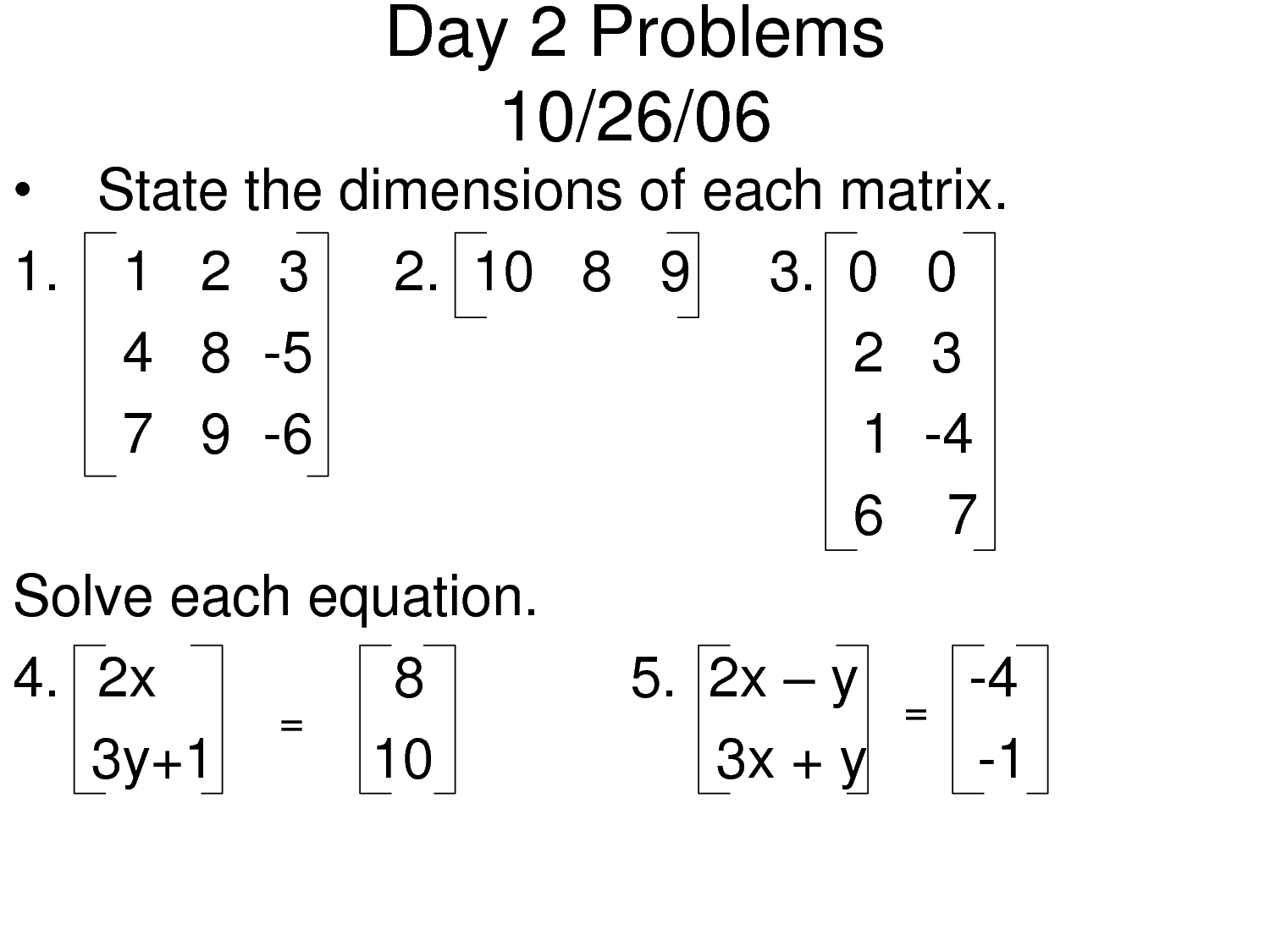
To solve matrices, the steps involve operations such as addition, subtraction, multiplication, and division. Begin by ensuring that the matrices have the same dimensions for addition and subtraction. For multiplication, check that the number of columns in the first matrix is equal to the number of rows in the second matrix. Perform the appropriate operations according to the rules of matrix arithmetic, and simplify the resulting matrix. For division, you can multiply by the inverse of the matrix instead, as division is not directly performed on matrices. Remember to verify your calculations and check for any errors in the process.
What are the different methods used to solve matrices?
The different methods used to solve matrices include Gaussian elimination, matrix inversion, Cramer's rule, LU decomposition, and eigenvalue decomposition. These methods involve various mathematical operations such as row operations, determinants, and factorizations to simplify and solve systems of linear equations represented by matrices. Each method has its own strengths and weaknesses depending on the specific properties of the matrix being solved.
How do you determine whether a matrix has a unique solution or not?
You determine whether a matrix has a unique solution by checking if the matrix is square and its determinant is non-zero. If a square matrix has a non-zero determinant, then the matrix has a unique solution. If the determinant is zero, the matrix either has no solution or infinitely many solutions, depending on the specific characteristics of the matrix.
What does it mean for a matrix to be invertible?
A matrix is invertible if there exists another matrix, called its inverse, such that when the original matrix is multiplied by its inverse, the result is the identity matrix. In other words, if matrix A is invertible, there exists matrix B such that A * B = B * A = I, where I is the identity matrix.
How can you find the inverse of a matrix?
To find the inverse of a matrix, you first calculate the determinant of the matrix and ensure that it is non-zero. Then, you find the matrix of minors, followed by the matrix of cofactors. Next, you transpose the matrix of cofactors to get the adjugate matrix. Finally, you multiply the adjugate matrix by 1/determinant to get the inverse matrix.
What is the significance of row operations in solving matrices?
Row operations are crucial in solving matrices as they allow us to manipulate the matrix in a systematic way without changing its solutions. By performing row operations such as swapping rows, multiplying a row by a nonzero scalar, or adding a multiple of one row to another, we can transform a matrix into simpler forms like row echelon or reduced row echelon form, making it easier to solve systems of linear equations, calculate determinants, and find inverses efficiently and accurately. These row operations help streamline the process of solving matrices by simplifying them into more manageable forms that reveal important information about the underlying linear system.
How do you use matrices to solve systems of linear equations?
To use matrices to solve systems of linear equations, the coefficients of the variables are arranged in a matrix along with the constants on the other side of the equal sign. This forms an augmented matrix. Then, row operations such as multiplying or adding rows are performed to transform the matrix into reduced row-echelon form or row-echelon form where the solutions can be easily identified. The values of the variables are then read directly from the matrix.
What is the role of determinants in solving matrices?
Determinants play a crucial role in solving matrices as they help determine if a matrix has an inverse (i.e., if it is invertible). A matrix is invertible if and only if its determinant is non-zero. Additionally, determinants are used to calculate the values of variables in systems of linear equations, find the area or volume of geometric figures, and determine the rank of a matrix. In essence, determinants are fundamental in understanding and manipulating matrices in various mathematical contexts.
Can matrices be used to solve nonlinear equations?
Matrices are typically used to solve systems of linear equations. Nonlinear equations are more complex and often require other methods such as numerical techniques or iterative approaches for solving them. Matrices can play a supporting role in these methods by providing a framework for organizing the data involved in the nonlinear equations.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.







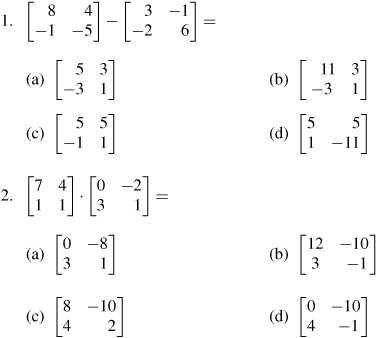
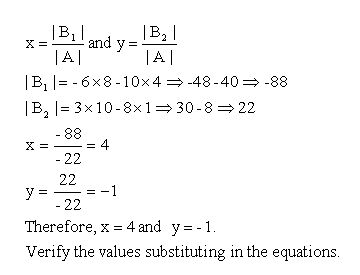















Comments