Solving Linear Equations Worksheets

Linear equations can be a challenging topic for students to grasp, but with the right resources, they can become more confident in their problem-solving skills. One valuable tool for reinforcing these concepts is solving linear equations worksheets. These worksheets provide practice problems and step-by-step guidance for students to work through, helping them develop a better understanding of this fundamental mathematical concept.

  Solving Two-Step Linear Equations Worksheets

---

  7th Grade Math Algebra Equations Worksheets

---

  Literal Equations Worksheet Answer Key

---

  Solving Equations with Parentheses Worksheet

---

  Graphing Linear Inequalities Worksheet

---

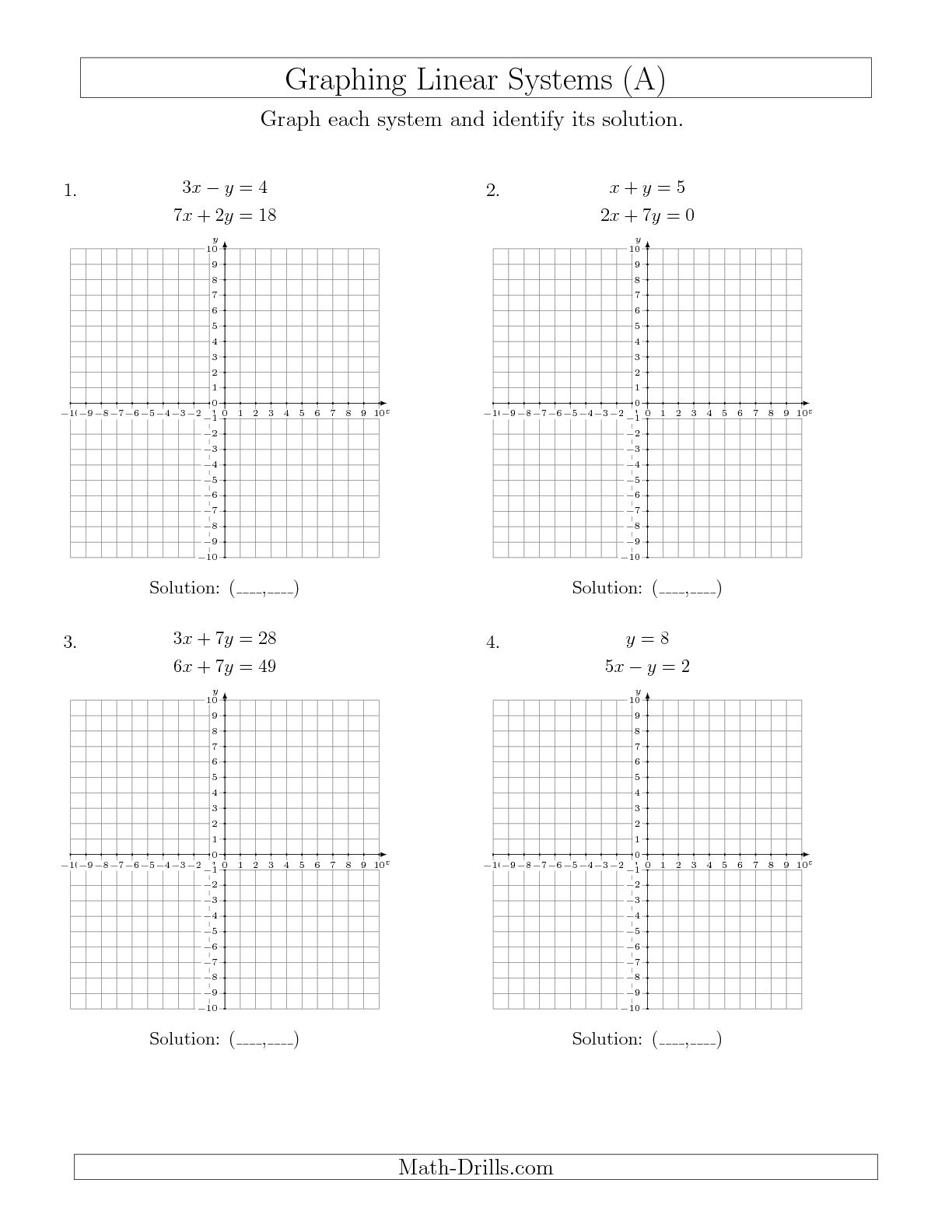
  Solving Systems of Linear Equations by Graphing

---

  7th Grade Math Word Problems

---

  Two-Step Equation Word Problems Worksheets

---

  7th Grade Math Worksheets Algebra

---

  Fun Algebra Puzzle Worksheets

---

  Kuta Software Infinite Algebra 1 Factoring Trinomials

---

  Holt Physical Science Chapter Review Answers

---

  Holt Physical Science Chapter Review Answers

---

  Holt Physical Science Chapter Review Answers

---

What is the purpose of solving linear equations?

The purpose of solving linear equations is to find the values of unknown variables that make the equation true. This helps in understanding and analyzing relationships between different quantities in various mathematical and real-world situations, such as calculating costs, determining quantities, and solving problems in science, engineering, and economics.

How do you determine the solution to a linear equation?

To determine the solution to a linear equation, you need to manipulate the equation to isolate the variable on one side and simplify the expression. This involves performing the same operation on both sides of the equation to keep it balanced. Once you have the variable isolated, you can easily compute its value. The solution is the value that makes the equation true when substituted back into the original equation.

What are the basic steps involved in solving a linear equation?

The basic steps involved in solving a linear equation are simplifying both sides of the equation by combining like terms, isolating the variable by performing inverse operations (such as addition, subtraction, multiplication, and division) to move constants to the other side of the equation, and finding the value of the variable that satisfies the equation. Finally, one must always check the solution by substituting it back into the original equation to ensure it is correct.

What is the difference between one-step and two-step linear equations?

The main difference between one-step and two-step linear equations is the number of operations required to solve them. One-step linear equations can be solved in just one operation, usually involving only addition or subtraction. On the other hand, two-step linear equations require two separate operations to isolate the variable, typically involving addition or subtraction followed by multiplication or division. In sum, one-step equations can be solved with a single step, while two-step equations require two steps to find the solution.

How do you handle fractions or decimals in linear equations?

When dealing with fractions or decimals in linear equations, it is important to first simplify the equation by clearing any fractions. This can be done by multiplying all terms in the equation by the least common multiple of all the denominators. To handle decimals, you can convert them to fractions by expressing them as a ratio of two integers. Once the equation is simplified, proceed with solving it using the standard methods such as substitution, elimination, or graphing.

Can you use the distributive property when solving linear equations?

Yes, the distributive property can be used when solving linear equations. It allows you to simplify expressions by distributing a factor across terms within parentheses. This property helps in combining like terms and isolating the variable in an equation, making it easier to solve for the unknown value.

What is the role of inverse operations in solving linear equations?

Inverse operations are essential in solving linear equations as they help isolate the variable by undoing the operations that have been performed on it. By applying inverse operations - such as addition and subtraction, multiplication and division - in a systematic manner, one can rearrange the equation to find the value of the variable. This allows for a step-by-step process to simplify and solve the equation, ultimately leading to finding the solution for the unknown variable.

How do you create a equation to represent a real-world problem?

To create an equation representing a real-world problem, first identify the variables involved and their relationships. Translate the problem into mathematical terms, assigning variables to unknown quantities. Use appropriate operations (addition, subtraction, multiplication, division) to model relationships between the variables. Follow the rules of algebra to represent the problem in equation form. Ensure the equation accurately captures the given problem and can be used to solve for the desired quantity.

Can linear equations have more than one solution?

No, linear equations can have only one solution if they intersect at a single point on a graph. If they are parallel lines or coincide with each other, they have either infinite solutions or no solutions.

How is graphing used in conjunction with solving linear equations?

Graphing is often used in conjunction with solving linear equations to visually represent the relationship between two variables and find the solution to the system of equations. By graphing the equations on a coordinate plane, the intersection point of the lines represents the solution to the system, which is the values where both equations are true simultaneously. This graphical method helps to visually see the solution and understand the relationship between the two linear equations.