Solving Equations with Exponents Worksheet
If you are a mathematics student who wants to improve your skills in solving equations with exponents, you have come to the right place. In this blog post, we will introduce you to a helpful worksheet that will assist you in mastering this concept. With clear and concise instructions, this worksheet is designed to provide you with ample practice on solving equations with exponents, ensuring that you have a strong foundation in this important topic.
Table of Images 👆
- 6th Grade Math Worksheets Algebra
- Algebra 1 Worksheets
- Math Worksheets for 9th Grade Algebra
- Multiplying and Dividing Decimals Worksheets
- Distributive Property Math Algebra Worksheets
- Simplifying Expressions Worksheets 7th Grade
- Factoring Trinomials Worksheet Answer Key
- Subtracting and Adding Linear Expressions Worksheet
- Graphing Absolute Value Equations Worksheet
- 7th Grade Math Worksheets Algebra
- 8th Grade Math Worksheets
- Solving Proportions Worksheet
- Rational Numbers Worksheets Grade 8
- 2006 Marcy Mathworks Punchline Algebra Answer Key
- Kuta Software Infinite Pre-Algebra Answers
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is an exponent?
An exponent is a mathematical operator that represents how many times a number (the base) is multiplied by itself. It is written as a small number placed to the upper right of the base number. The exponent indicates the power to which the base is raised. For example, in 2^3, 2 is the base and 3 is the exponent, meaning 2 is multiplied by itself 3 times.
How do you solve equations with exponents?
To solve equations with exponents, you first need to isolate the term with the exponent by moving all other terms to the other side of the equation. Then, you can use properties of exponents, such as the power rule, to simplify the equation. Finally, solve for the variable by taking the appropriate root or applying the inverse operation to the exponent. Remember to keep track of any negative exponents and perform all operations carefully to find the solution to the equation.
Can you solve equations with negative exponents? If so, how?
Yes, equations with negative exponents can be solved by applying the property of negative exponents which states that a term with a negative exponent can be rewritten as the reciprocal of the term with a positive exponent. For example, if you have x^-3 in an equation, you can rewrite it as 1/x^3. By manipulating the expressions in this way, you can simplify the equation and solve for the unknown variable.
What is the difference between solving equations with exponents and solving equations without exponents?
When solving equations with exponents, you may need to apply rules for manipulating exponents, such as the power rule or the product rule. This involves simplifying expressions by combining like terms and following the proper procedures for performing operations with exponents. On the other hand, when solving equations without exponents, you typically work with basic arithmetic operations such as addition, subtraction, multiplication, and division. The presence of exponents adds an additional layer of complexity to the equation-solving process, requiring a good understanding of exponent rules to arrive at the correct solution.
How do you simplify expressions with exponents before solving the equation?
To simplify expressions with exponents before solving the equation, you first need to apply the rules of exponents. This involves combining like terms, multiplying and dividing bases with the same exponents, and raising a base with an exponent to another exponent. By simplifying the expression, you can make the equation easier to work with and solve for the variable. Remember to follow the order of operations and consider applying different exponent rules to make the process smoother.
What are some common strategies for solving equations with exponents?
Some common strategies for solving equations with exponents include isolating the term with the exponent, using the properties of exponents to simplify the equation, applying inverse operations to both sides of the equation, using the power rule to combine exponents, and recognizing patterns that allow for factoring or rewriting the equation in a simpler form. Additionally, logarithms can be used to solve exponential equations by converting them into a linear form.
Can you have fractions or decimals as exponents? If so, how do you solve the equation?
Yes, you can have fractions or decimals as exponents. To solve an equation with a fraction or decimal exponent, you can convert it into a different form depending on the context - for example, you can rewrite a fraction exponent as a root or use the logarithm function. If you have a decimal exponent, you can also convert it into a fraction and then apply the appropriate mathematical operations. Be sure to follow the rules of exponents and use algebraic techniques to simplify the equation and find the solution.
What is the process for solving equations with variable exponents?
When solving equations with variable exponents, the goal is typically to isolate the variable on one side of the equation. Begin by applying properties of exponents, such as using the property \(a^{m} \cdot a^{n} = a^{m+n}\) to simplify the expression. Next, try to rewrite the equation with the variables having the same base by manipulating the exponents. Once the exponents have the same base, set the exponents equal to each other and solve for the variable. The final step is to substitute the found value back into the original equation to verify the solution.
Are there any restrictions or limitations when solving equations with exponents?
Yes, there are some limitations when solving equations with exponents. One common restriction is that when solving equations with fractional exponents, the base must be a non-negative real number in order to ensure that the roots are real. Additionally, when working with complex numbers, the rules for simplifying equations with exponents can differ from those for real numbers, leading to additional limitations and considerations when solving equations involving complex exponential expressions.
Can you check the solution to an equation with exponents? If so, how do you do it?
Yes, to check the solution to an equation with exponents, you simply substitute the solution back into the original equation and verify that it satisfies the equation. Ensure that you correctly apply the exponent rules when substituting the solution. If the solution makes the equation true, then it is a valid solution to the equation.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.










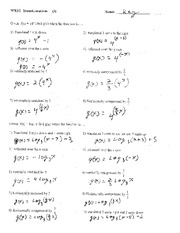




















Comments