Solving Complex Equations Worksheet
Equations can often be complex and challenging to solve, especially for those who struggle with math. If you find yourself needing extra practice or guidance in this area, a solving complex equations worksheet might be just what you need. Designed to provide targeted practice on this specific topic, these worksheets offer a systematic approach to help learners grasp the concepts and improve their problem-solving skills.
Table of Images 👆
- Solving Quadratic Equations Worksheet
- Two-Step Equations Worksheet
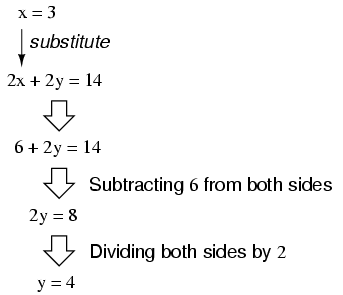
- Substitution Equations Worksheets
- Solving Polynomials Worksheet
- Complex Conjugate Imaginary Numbers
- Algebra 2 Solving Quadratic Equations
- Solving Proportions Worksheet Answers
- Algebra Linear Equations Worksheet
- How Do You Solve Radical Equations
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the purpose of solving complex equations?
The purpose of solving complex equations is to find solutions to problems in various fields such as mathematics, physics, engineering, economics, and more. By solving complex equations, we can understand relationships, make predictions, optimize processes, and model real-world situations accurately. It allows us to analyze complex systems and make informed decisions based on the results obtained from solving these equations.
How do you define a complex equation?
A complex equation is an equation that involves complex numbers, which have a real part and an imaginary part. These equations typically include terms with variables raised to powers that include the imaginary unit "i" (√(-1)), as well as constants that may be complex numbers. Complex equations can have solutions that are complex numbers, and may involve operations such as addition, subtraction, multiplication, division, and exponentiation of complex numbers.
What are some common methods for solving complex equations?
Some common methods for solving complex equations include using algebraic manipulation techniques such as factoring, combining like terms, and isolating variables, as well as applying properties of exponents and logarithms. Other methods involve graphical representation of equations to identify intersections, substitution of variables, using the quadratic formula for quadratic equations, and employing numerical methods like Newton's method or the bisection method for root-finding. Additionally, techniques like completing the square and partial fraction decomposition can be utilized for solving specific types of equations.
Can complex equations have multiple solutions? If yes, why?
Yes, complex equations can have multiple solutions because the complex number system includes real and imaginary components, allowing for multiple valid solutions to exist that satisfy the equation. This is particularly evident in polynomial equations, where the fundamental theorem of algebra states that an nth-degree polynomial equation can have up to n roots or solutions, some of which may be complex numbers.
How do you simplify complex equations before solving them?
To simplify complex equations before solving them, start by combining like terms, distributing any constants, and applying the order of operations. Then, try to factor out any common terms, group together similar terms, and simplify any fractions or exponents present in the equation. This will help make the equation easier to solve by reducing the number of terms and making the algebraic manipulation more manageable.
When should you use the quadratic formula to solve complex equations?
You should use the quadratic formula to solve complex equations when you have a quadratic equation in the form of ax^2 + bx + c = 0, where a, b, and c are constants. This formula is particularly useful when factoring or completing the square is not practical or possible. The quadratic formula is: x = (-b ± √(b^2 - 4ac)) / 2a, and it provides the exact solutions for quadratic equations, including complex roots if necessary.
Can complex equations have imaginary solutions? If yes, what do they represent?
Yes, complex equations can have imaginary solutions. Imaginary solutions represent numbers involving the square root of -1, denoted by the imaginary unit "i". These solutions often arise when solving equations that involve taking square roots of negative numbers or when dealing with problems in physics and engineering that involve oscillatory behavior or certain types of waves. The combination of real and imaginary numbers in a complex solution provides a deeper understanding of the behavior and properties of the system being analyzed.
What are the steps involved in solving a complex equation using the substitution method?
To solve a complex equation using the substitution method, first identify a variable to substitute with another expression. Next, replace that variable in the equation with the new expression. Then, simplify the equation by performing the necessary operations to isolate the variable. Finally, solve for the variable by using algebraic techniques such as factoring, distributing, or combining like terms. Repeat these steps as needed until the equation is fully simplified and the variable is isolated, arriving at a solution for the equation.
How can you verify if the solution to a complex equation is valid?
To verify if the solution to a complex equation is valid, you can substitute the solution back into the original equation and solve for both the real and imaginary parts separately. If the substituted values satisfy both parts of the equation, then the solution is valid. Additionally, you can also check if the solution satisfies any special conditions or constraints specified in the problem.
Are there any limitations or restrictions when it comes to solving complex equations?
When solving complex equations, some limitations and restrictions may include difficulty in finding exact solutions, particularly for equations with multiple variables or non-linear terms. Additionally, some equations may have no solutions, infinitely many solutions, or only approximate solutions. The complexity of the equation and the availability of appropriate techniques or tools can also present challenges in finding solutions.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.







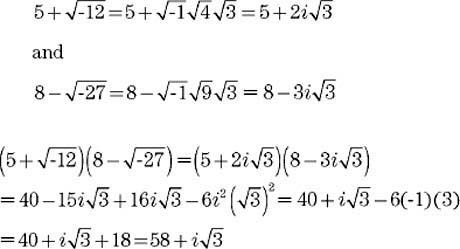

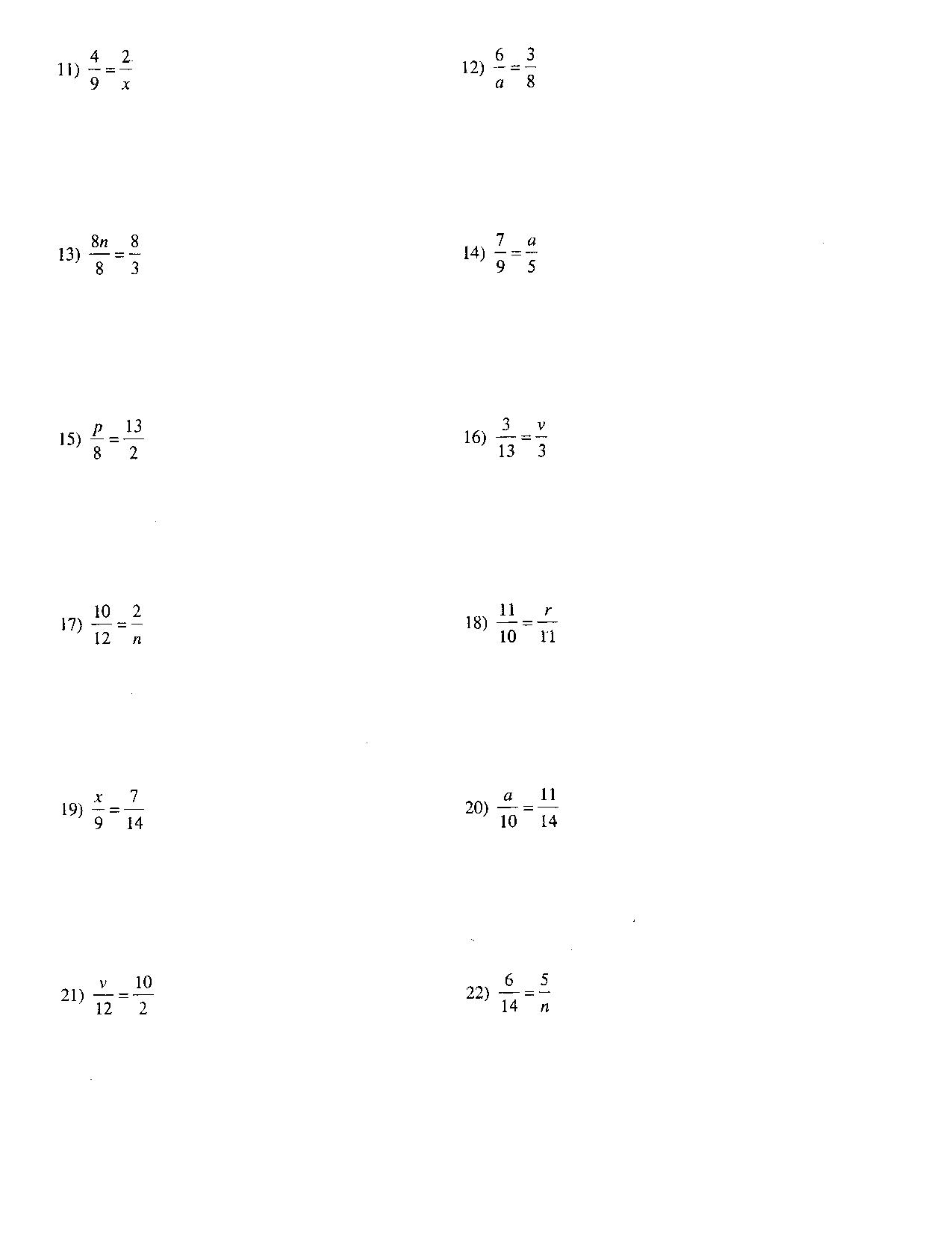
















Comments