Slope -Intercept Formula Worksheet

Are you a math teacher searching for an engaging way to teach your students about the slope-intercept formula? Look no further! This blog post provides a descriptive and declarative overview of worksheets available for teaching the slope-intercept formula to your students. Whether you are a teacher looking for additional resources or a student seeking extra practice, these worksheets are designed to help deepen your understanding of this important concept.

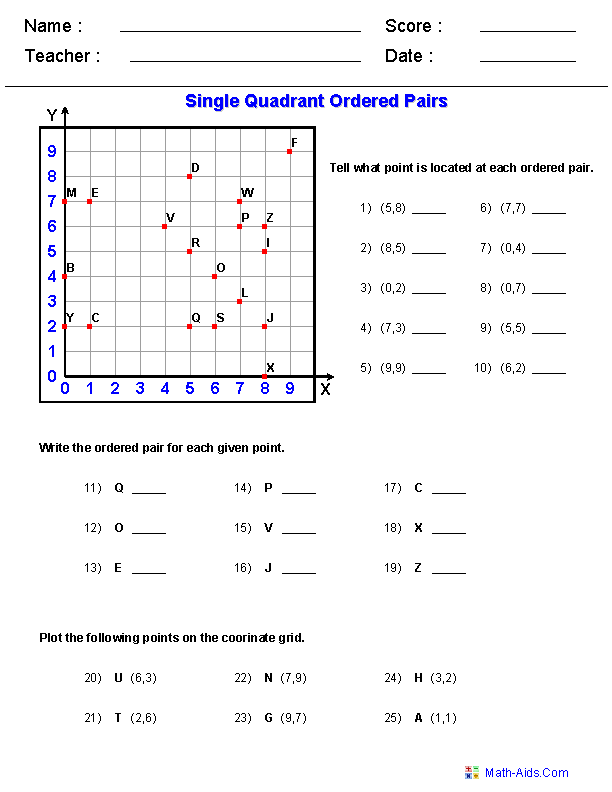
  5th Grade Graphing Ordered Pairs Worksheet

---

  Kuta Software Worksheets

---

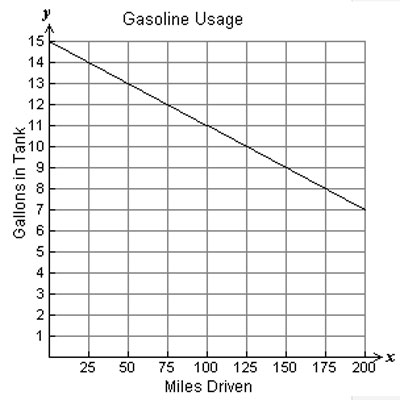
  Real Life Linear Graphs Examples

---

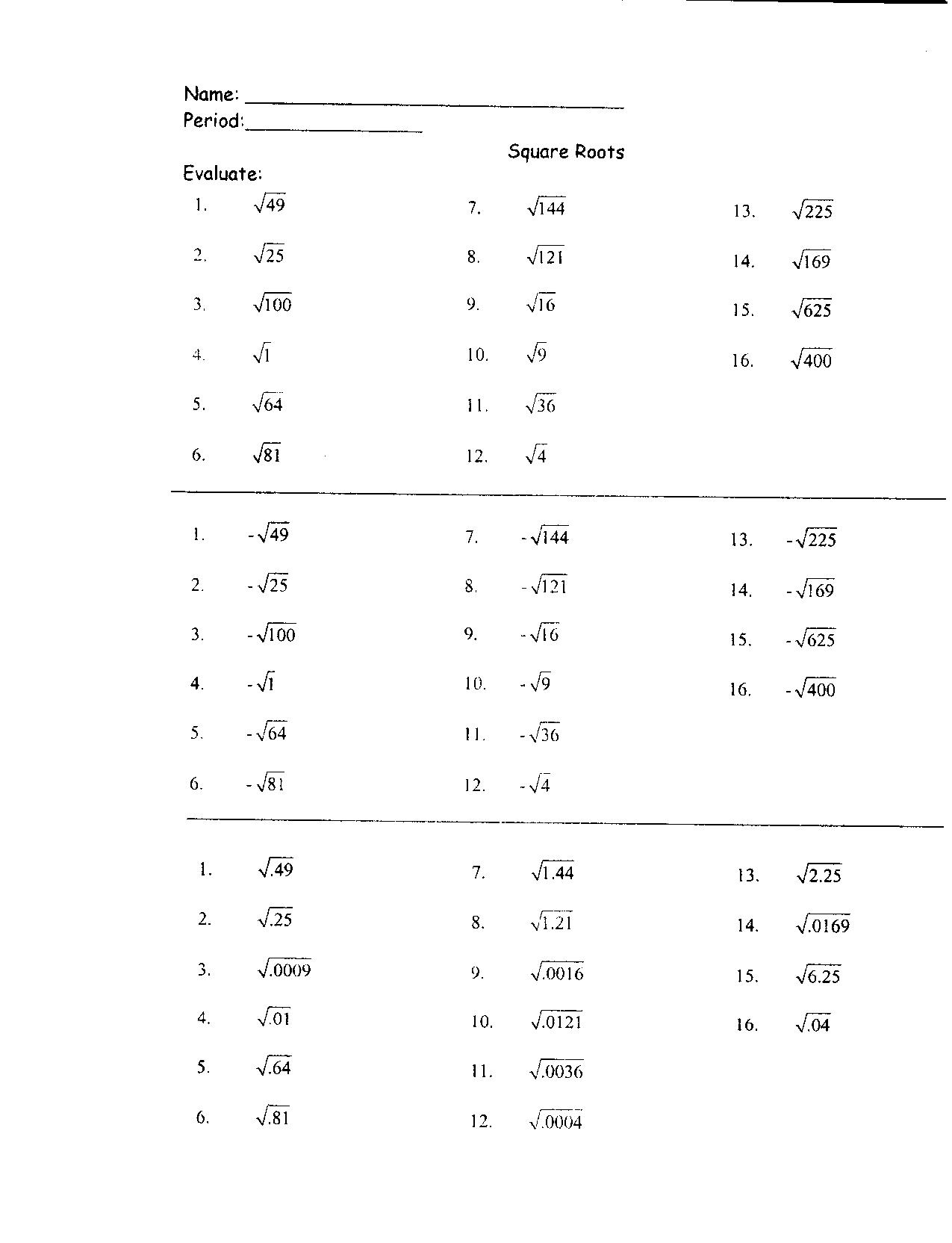
  Perfect Square Roots Worksheet

---

  Science Worksheets 6th Grade Notes

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

  5th Grade Math Reference Sheet

---

What is the slope-intercept formula?

The slope-intercept formula is the equation of a straight line in the form y = mx + b, where m represents the slope of the line and b represents the y-intercept, which is the point where the line intersects the y-axis. This formula is commonly used to graph lines and find the equation of a line given its slope and y-intercept.

How do you determine the slope from a linear equation in slope-intercept form?

To determine the slope from a linear equation in slope-intercept form (y = mx + b), you simply need to look at the coefficient of x, which is represented by 'm'. The slope of the line is equal to 'm', as it represents the rate at which the line is ascending or descending. Thus, the slope in a linear equation in slope-intercept form is the coefficient of x (m).

How do you determine the y-intercept from a linear equation in slope-intercept form?

To determine the y-intercept from a linear equation in slope-intercept form (y = mx + b), you simply look at the constant term "b" in the equation. The value of "b" represents the y-coordinate where the line intersects the y-axis, which is the y-intercept. Therefore, the value of "b" is the y-intercept of the line.

Can the slope be negative or zero in the slope-intercept form?

Yes, the slope in the slope-intercept form can be negative, positive, or zero. The slope, represented by the coefficient of x in the equation y = mx + b, determines the direction and steepness of the line. A negative slope indicates a line that slopes downward from left to right, a positive slope indicates a line that slopes upward from left to right, and a slope of zero indicates a horizontal line.

What does the slope represent in the context of a linear equation?

In the context of a linear equation, the slope represents the rate at which the dependent variable changes with respect to the independent variable. It indicates how steep or gradual the line is inclined and is an essential measure of the relationship between the two variables. A positive slope signifies a positive correlation between variables, while a negative slope indicates a negative correlation. The slope can also be interpreted as the coefficient of the independent variable in the equation and helps in predicting future values based on the given data points.

What does the y-intercept represent in the context of a linear equation?

The y-intercept of a linear equation represents the point where the graph intersects the y-axis. It is the value of y when x is equal to zero, indicating the initial value of y when no other factors are present. In real-world applications, the y-intercept can represent a starting point, an initial value, or a constant term that influences the relationship between x and y.

How do you graph an equation in slope-intercept form?

To graph an equation in slope-intercept form (y = mx + b), start by plotting the y-intercept on the y-axis at the point (0, b). Next, use the slope (m) to find a second point by moving up (if m is positive) or down (if m is negative) the graph according to the rise over run ratio. Connect the two points with a straight line to graph the equation. Repeat the process for additional lines or points if needed to accurately represent the equation.

Can you use the slope-intercept form to find the x-intercept of a linear equation?

Yes, the slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. To find the x-intercept, you set y = 0 and solve for x. By setting y = 0 in the equation y = mx + b, you can solve for x to find the x-intercept.

How do you convert a linear equation in standard form to slope-intercept form?

To convert a linear equation in standard form (Ax + By = C) to slope-intercept form (y = mx + b), first solve for y in the standard form equation. Start by subtracting Ax from both sides to isolate By. Then divide by B to get y in terms of x. This will give you y = (-A/B)x + C/B. Finally, rearrange the equation to have y on the left side in terms of x on the right side, which will be in slope-intercept form.

Can you write the equation of a line in slope-intercept form if you are given the slope and a point on the line?

Yes, if you are given the slope \( m \) and a point \( (x_1, y_1) \) on the line, you can use the point-slope form of a line equation to find the equation of the line. The equation in slope-intercept form is \( y - y_1 = m(x - x_1) \), which you can simplify to \( y = mx + (y_1 - mx_1) \). This is the equation of the line passing through the point \( (x_1, y_1) \) with slope \( m \).