Similar Triangles Worksheet

The Similar Triangles Worksheet is an invaluable tool for students seeking to solidify their understanding of this important geometric concept. Designed for middle and high school students, this worksheet provides a comprehensive set of exercises that allow learners to practice identifying and working with similar triangles. With its clear instructions and diverse range of questions, this worksheet offers a thorough review of the topic, making it suitable for both classroom use and independent study.

  Similar Triangles and Polygons Worksheet

---

  Right Triangle Pythagorean Theorem Worksheets

---

  Similar Figures 7th Grade Worksheets

---

  Congruent Triangles Worksheet

---

  Similar Right Triangles Worksheet

---

  Similar Figures Proportions Worksheet

---

  Similar Triangle Proofs Worksheet

---

  Geometry Similar Triangles Worksheet

---

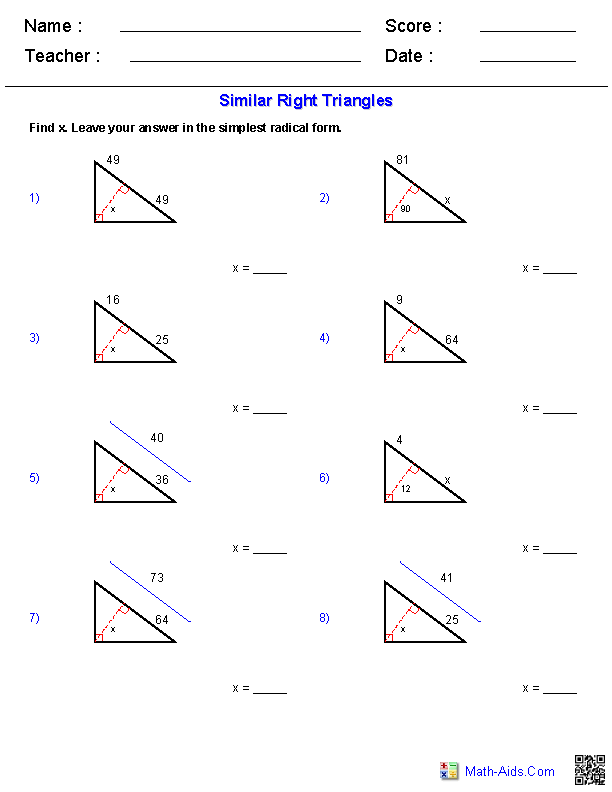
Define similar triangles.

Similar triangles are two triangles that have the same shape but can be different sizes. This means that their corresponding angles are equal and their corresponding sides are in proportion to each other.

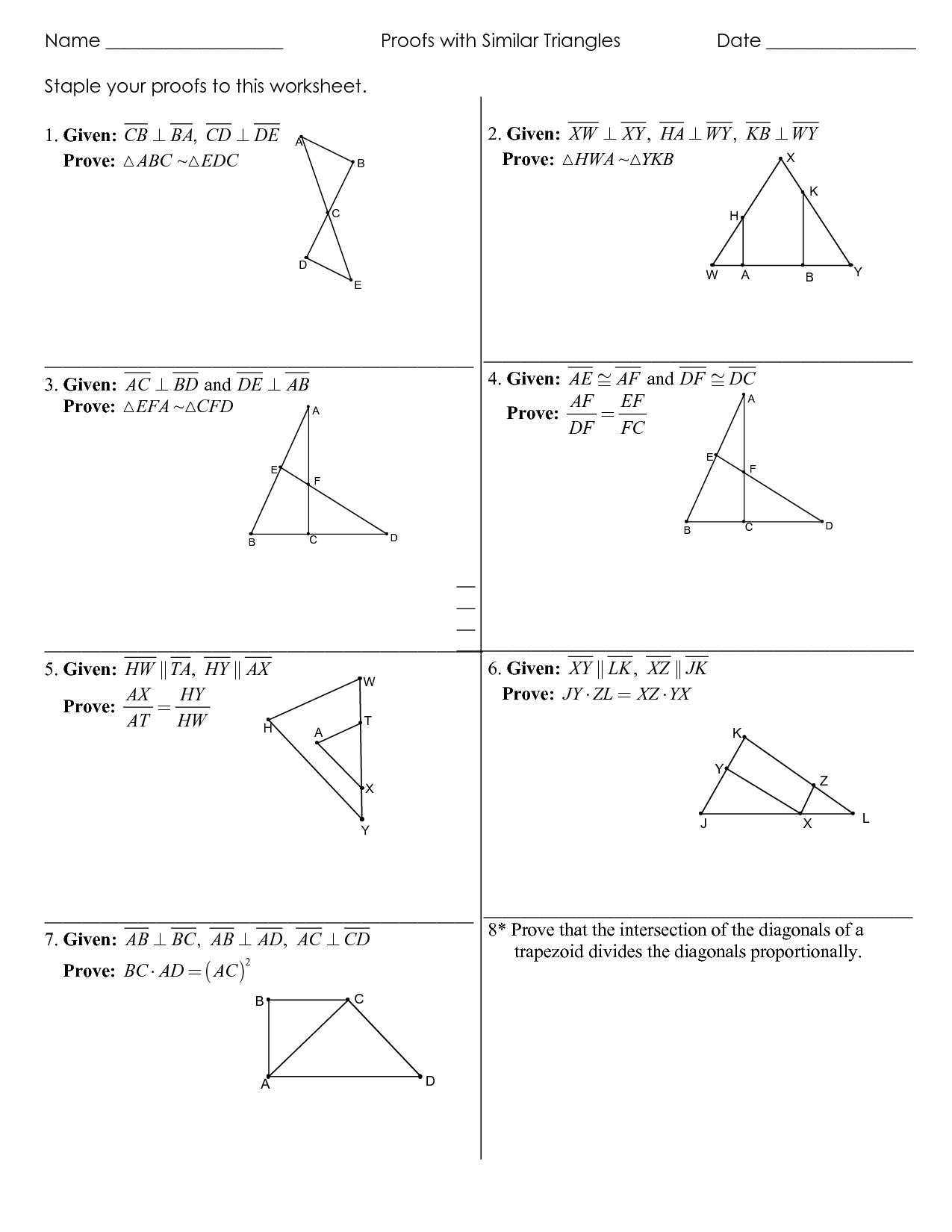
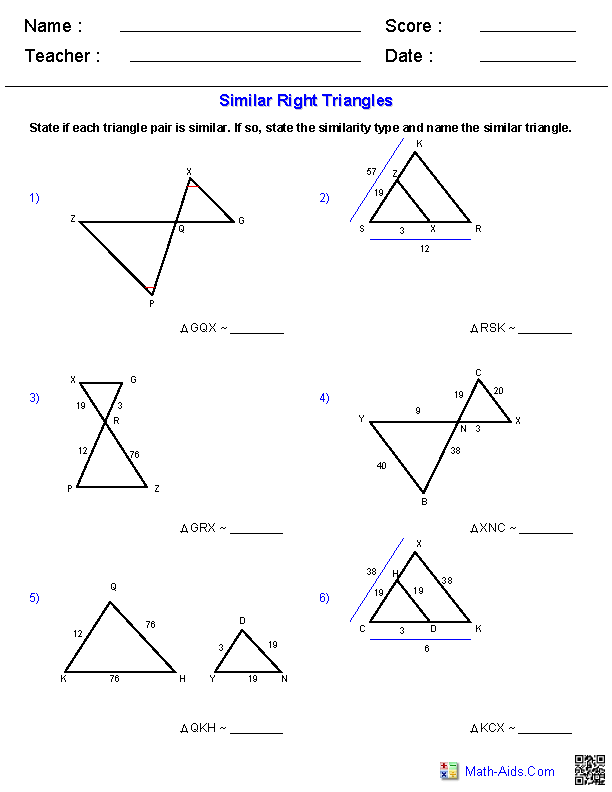
State the criteria for two triangles to be similar.

Two triangles are similar if their corresponding angles are congruent and their corresponding sides are in proportion, meaning that the ratios of the lengths of their corresponding sides are equal. This is known as the Angle-Angle (AA) or Side-Angle-Side (SAS) similarity criteria.

Explain the concept of corresponding angles in similar triangles.

Corresponding angles in similar triangles are angles that are positioned in the same location within each respective triangle and have the same measure. This means that if two triangles are similar, their corresponding angles will be congruent. For example, if angle A in triangle ABC is congruent to angle D in triangle DEF, and angle B in triangle ABC is congruent to angle E in triangle DEF, then the triangles are similar. This property is essential in proving the similarity of triangles and applying geometric rules and theorems in various problems involving similar triangles.

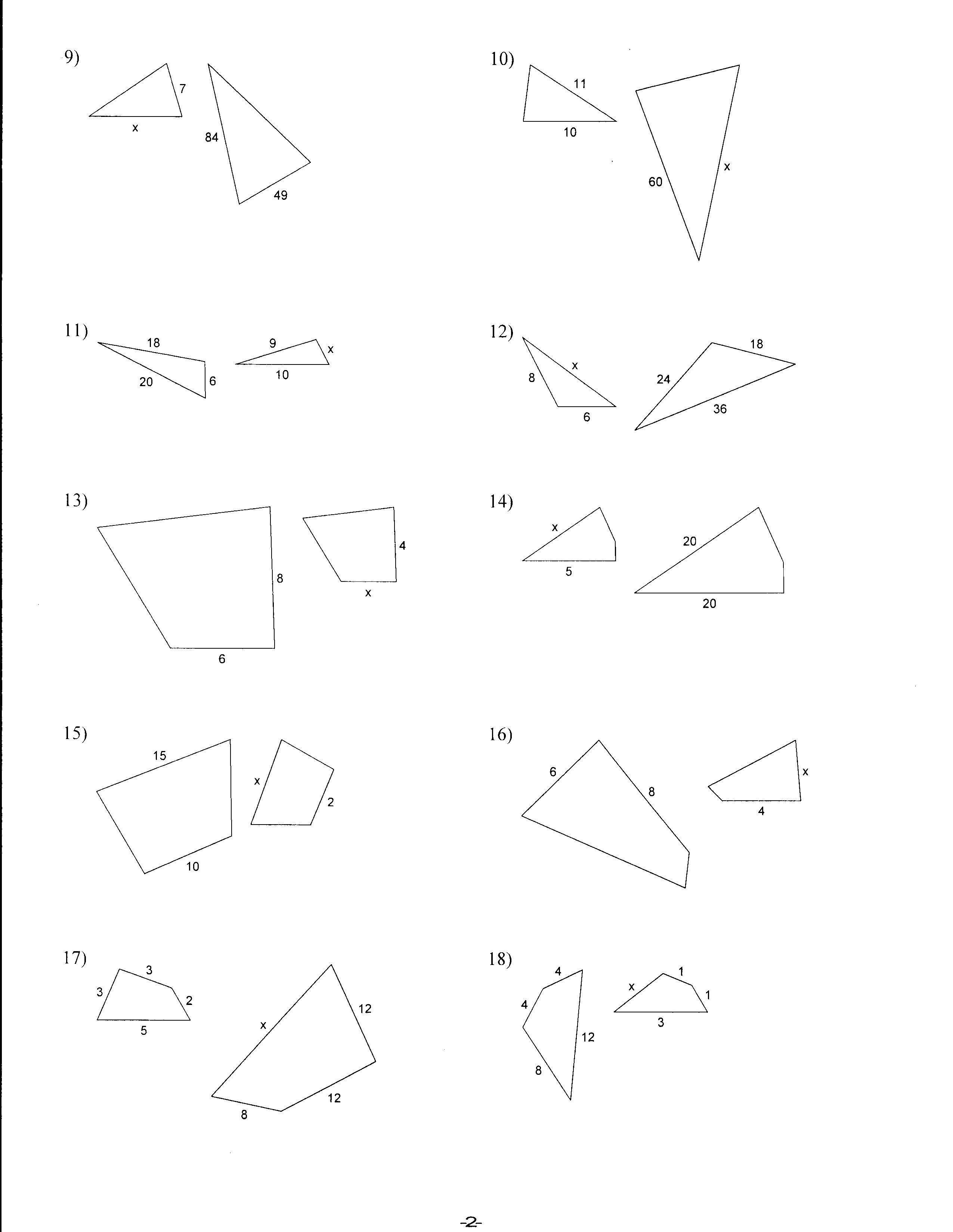
Describe the relationship between the sides of similar triangles.

The relationship between the sides of similar triangles is known as the corresponding sides ratio. In similar triangles, the corresponding sides are in proportion to each other, meaning that all the corresponding sides have the same ratio. This ratio is constant for all pairs of sides in similar triangles, and it is used to determine the length of one side if the length of another is known. This fundamental property helps us understand and work with similar triangles in geometry and trigonometry.

How can we use similarity to find unknown side lengths in a triangle?

You can use similarity in a triangle to find unknown side lengths by setting up proportions between corresponding sides of similar triangles. By identifying similar triangles within a larger triangle, you can create ratios of corresponding sides and use these ratios to solve for missing side lengths. This method, known as the Triangle Proportionality Theorem, allows you to find unknown side lengths by comparing the relationships between the sides of similar triangles.

Discuss the significance of the scale factor in similar triangles.

The scale factor in similar triangles is significant because it represents the ratio of corresponding sides of the two triangles. This means that if you know the scale factor between two similar triangles, you can use it to determine the proportional relationship between their sides. The scale factor also allows you to predict the length of unknown sides in one triangle if you know the lengths of corresponding sides in the other triangle. Overall, the scale factor is essential in understanding and working with similar triangles, as it provides a clear and consistent way to compare their dimensions and properties.

Explain how to determine if two triangles are similar given their angles.

To determine if two triangles are similar based on their angles, you need to check if all corresponding angles are congruent. If the three angles of one triangle are equal in measure to the three corresponding angles of the other triangle, then the two triangles are similar. This is known as the Angle-Angle (AA) similarity criterion, which states that if two angles of one triangle are equal in measure to two angles of another triangle, then the third angles of the triangles must also be equal, leading to similarity.

What is the importance of the Angle-Angle (AA) criterion in determining similarity?

The Angle-Angle (AA) criterion is important in determining similarity because if two triangles have two corresponding angles that are congruent, then the third angle must also be congruent due to the fact that the sum of the angles in a triangle is always 180 degrees. This criterion allows us to conclude that the two triangles are similar based on angle congruency alone, without having to measure the lengths of the sides. Essentially, the AA criterion simplifies and speeds up the process of determining similarity between triangles.

Describe the concept of the Side-Angle-Side (SAS) criterion for similarity.

The Side-Angle-Side (SAS) criterion for similarity states that if two triangles have two pairs of sides that are proportional in length and the included angles formed by these sides are congruent, then the triangles are similar. This criterion provides a way to determine when two triangles are similar based on a combination of side lengths and angles.

Explain the difference between two triangles being similar and congruent.

Similar triangles have the same shape but not necessarily the same size, meaning their corresponding angles are equal and their corresponding sides are proportional. On the other hand, congruent triangles have exactly the same shape and size, with all angles and sides being equal. In essence, similar triangles are related by proportionality, while congruent triangles are identical in shape and size.