Similar Polygons Worksheet and Answers

Are you a student or educator searching for a valuable resource to enhance your understanding of similar polygons? Look no further as we present to you the Similar Polygons Worksheet and Answers. This comprehensive worksheet is designed to help both students and educators delve deep into the concept of similar polygons and strengthen their knowledge in this area.

  Similar Triangles and Polygons Worksheet

---

  Similar Polygons Worksheet

---

  Similar Figures 7th Grade Worksheets

---

  Kuta Software Infinite Geometry Answer Key Similar Polygons

---

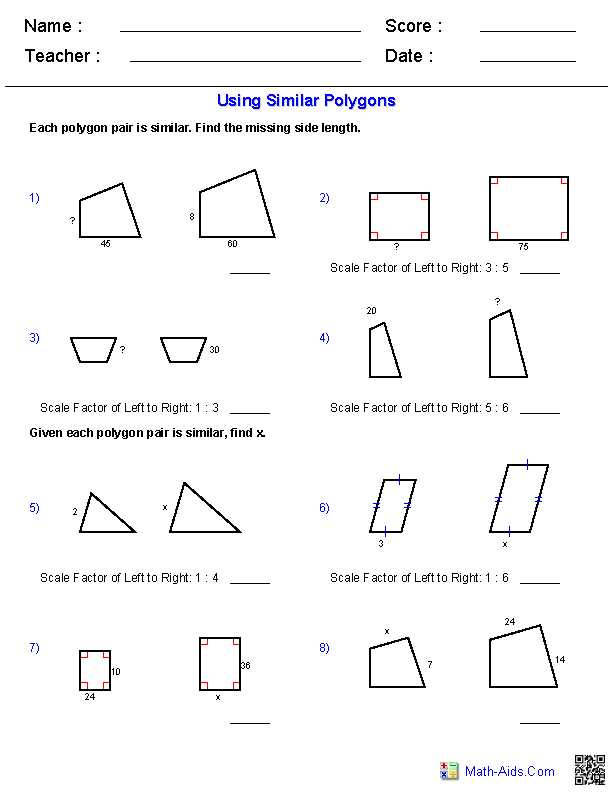
  Using Similar Polygons Worksheet

---

  Congruent Similar Polygons Worksheet

---

  Similar Polygons Worksheet

---

  Congruent and Similar Polygons Worksheets

---

  Geometry Similar Polygons Worksheet

---

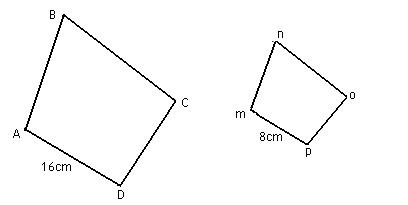
What is a similar polygon?

A similar polygon is a polygon that has the same shape as another polygon, but not necessarily the same size. The corresponding angles of similar polygons are equal, and the corresponding sides are in proportion to each other.

How can you determine if two polygons are similar?

Two polygons are considered similar if their corresponding angles are congruent and their corresponding sides are in proportion. This means that you would need to check if all angles of one polygon are equal to the corresponding angles of the other polygon, and if the ratios of the lengths of their sides match. If these conditions are met, then the two polygons are similar.

What is the significance of corresponding angles in similar polygons?

Corresponding angles in similar polygons are significant because they are congruent, meaning they have the same measure. This property helps establish a proportional relationship between the sides of the similar polygons, allowing us to determine the scale factor by comparing corresponding sides. This is key in various geometric problems, such as finding missing side lengths or angles in similar figures, and understanding the relationship between different sizes of the same shape.

What are corresponding sides in similar polygons?

Corresponding sides in similar polygons are sides that are in the same relative position to each other in each polygon. This means that the sides are proportional in length and have the same relative orientation or angle measure, even though the polygons are not necessarily congruent.

How do you find the scale factor between two similar polygons?

To find the scale factor between two similar polygons, you can compare the corresponding side lengths of the polygons. The scale factor is calculated by dividing the length of a side on one polygon by the corresponding length on the other polygon. The scale factor will be the same for all pairs of corresponding sides of the similar polygons.

How does changing the dimensions of one polygon affect the corresponding dimensions of the other polygon in similar polygons?

Changing the dimensions of one polygon in similar polygons results in a proportional change in the corresponding dimensions of the other polygon. This means that if one side of a polygon is increased or decreased by a certain factor, then the corresponding side of the other polygon will also be increased or decreased by the same factor to maintain the similarity between the two polygons.

Can two polygons be similar if one is a reflection of the other?

Yes, two polygons can be similar if one is a reflection of the other. Similarity of polygons depends on having the same shape, but not necessarily the same orientation or position. So, if one polygon is a reflection of the other, they can still have proportional sides and equal corresponding angles, which are characteristics of similar polygons.

Can two polygons be similar if one is a rotation of the other?

Yes, two polygons can be similar even if one is a rotation of the other. Similarity of polygons is determined by the corresponding angles being equal and the sides being proportional in length, so a rotation does not alter these properties. As long as the angles and side-length ratios remain the same, the polygons are still considered similar regardless of any rotation.

How can you use similar polygons to solve problems involving ratios and proportions?

Similar polygons have corresponding angles that are equal and corresponding sides that are proportional. By identifying corresponding sides and setting up ratios between them, you can solve problems involving ratios and proportions. For example, if you have two similar triangles, you can set up a proportion by equating the ratios of corresponding sides to find the unknown side length. This concept can be extended to solving various geometric problems involving areas, perimeters, and measurements using the properties of similar polygons.

In what real-life applications are similar polygons used?

Similar polygons are used in a variety of real-life applications, including cartography for creating maps, architecture for scaling building designs, computer graphics for creating realistic images, and engineering for designing structures that maintain proportional relationships. Additionally, similar polygons are utilized in areas such as urban planning, landscaping, and video game development to accurately represent and scale objects and environments.