Sequences Worksheet 6th Grade
Are you a 6th-grade student or a parent looking for a way to practice and reinforce your understanding of sequences? If so, you've come to the right place. In this blog post, we will explore the importance of worksheets as a valuable learning tool for mastering the concepts of sequences.
Table of Images 👆
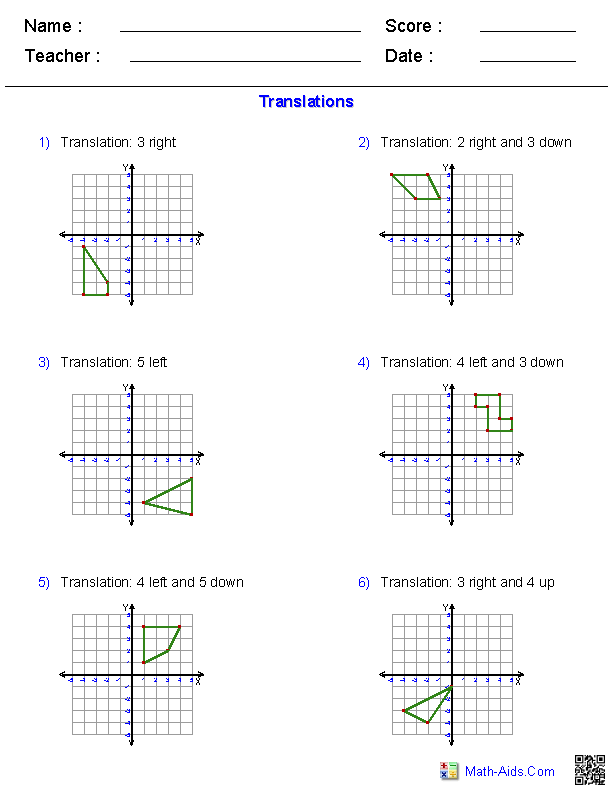
- Geometry Translations Worksheet
- Decimal Multiplication Worksheets
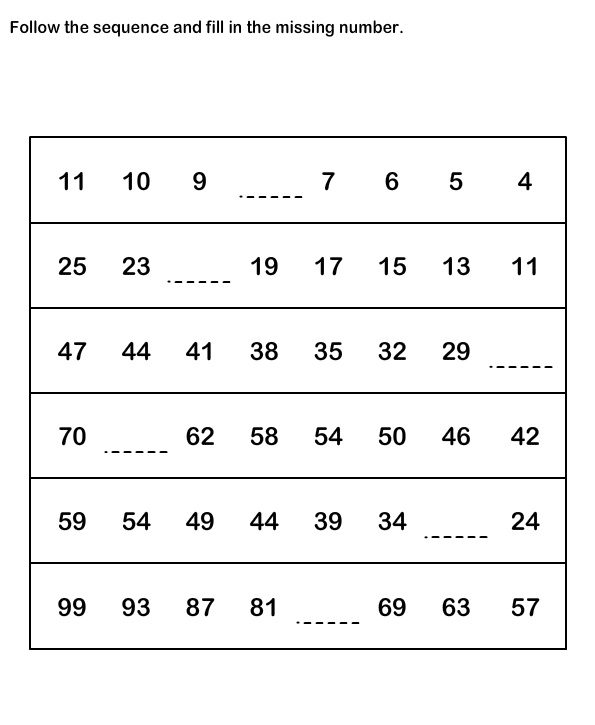
- Number Sequence Worksheets Free
- First Grade Pattern Math Worksheets
- Prime Factor Worksheets 5th Grade
- 3rd Grade Math Test Printable
- Free 2nd Grade Math Coloring Pages
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
- Geometric Pattern Vector Art
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is a sequence?
A sequence is a collection of numbers or objects arranged in a specific order based on a rule or pattern. Each element in the sequence follows a predetermined relationship to the previous elements, allowing for the prediction and continuation of the sequence.
How is a sequence different from a series?
A sequence is a list of numbers that follow a specific pattern or rule, while a series is the sum of the terms in a sequence. In other words, a sequence is the list of individual elements, whereas a series is the result of adding those individual elements together.
What is an arithmetic sequence?
An arithmetic sequence is a sequence of numbers in which each term is obtained by adding a common difference to the previous term. The common difference is a fixed number that determines how the sequence progresses, making it so that each term is a constant interval apart from the previous one.
How can you find the common difference in an arithmetic sequence?
To find the common difference in an arithmetic sequence, subtract any term in the sequence from the term that comes right after it. The result of this subtraction will give you the common difference between consecutive terms in the arithmetic sequence.
What is a geometric sequence?
A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. The general form of a geometric sequence is given as \(a_n = a_1 \cdot r^{(n-1)}\), where \(a_1\) is the first term, \(r\) is the common ratio, and \(n\) is the term number.
How can you find the common ratio in a geometric sequence?
To find the common ratio in a geometric sequence, you divide any term in the sequence by the preceding term. The common ratio (r) is constant and will remain the same no matter which terms in the sequence you choose to compare. Mathematically, if the terms in a geometric sequence are denoted as a, ar, ar^2, ar^3, ..., then the common ratio is given by r = (ar)/(a).
What is the nth term of a sequence?
The nth term of a sequence refers to the formula that allows you to find the value of any term in the sequence based on its position. It is typically expressed as a function of n, where n represents the position of the term in the sequence. By plugging in a specific value for n, you can calculate the corresponding term in the sequence using the nth term formula.
How can you find the nth term in an arithmetic sequence?
To find the nth term in an arithmetic sequence, you can use the formula: \( a_n = a_1 + (n-1) \times d \), where \( a_n \) represents the nth term, \( a_1 \) is the first term of the sequence, \( n \) is the position of the term you want to find, and \( d \) is the common difference between terms in the sequence. Plug in the values of \( a_1 \), \( n \), and \( d \) into the formula to calculate the nth term in the arithmetic sequence.
How can you find the nth term in a geometric sequence?
To find the nth term in a geometric sequence, you can use the formula \(a_{n} = a_{1} \times r^{n-1}\), where \(a_{n}\) represents the nth term, \(a_{1}\) is the first term in the sequence, \(r\) is the common ratio between consecutive terms, and \(n\) is the position of the term you want to find. This formula allows you to calculate any term in the sequence based on the initial term and the common ratio.
How can you determine if a given sequence is an arithmetic or geometric sequence?
To determine if a given sequence is an arithmetic or geometric sequence, you can look for a common difference between consecutive terms in an arithmetic sequence or a common ratio between consecutive terms in a geometric sequence. In an arithmetic sequence, the difference between consecutive terms is constant, while in a geometric sequence, the ratio between consecutive terms is constant. By calculating the differences or ratios between terms in the sequence, you can identify whether it follows an arithmetic or geometric pattern.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






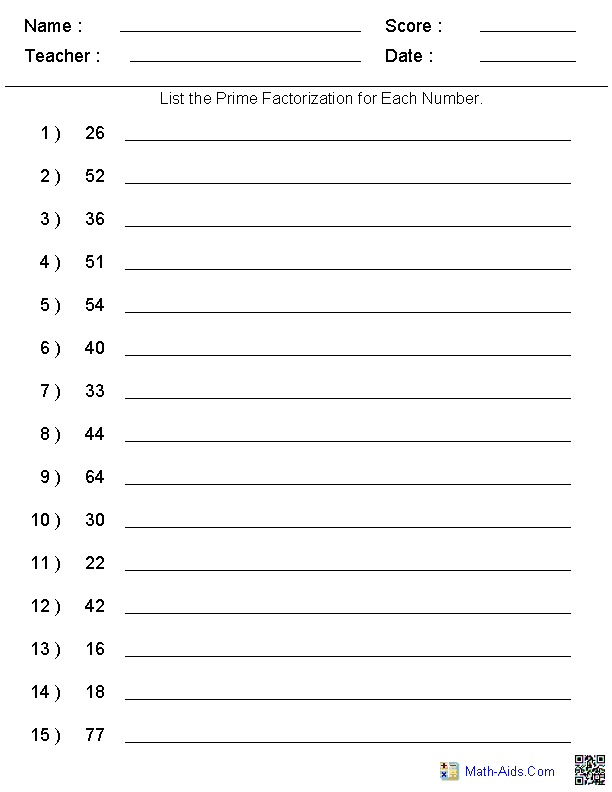



























Comments