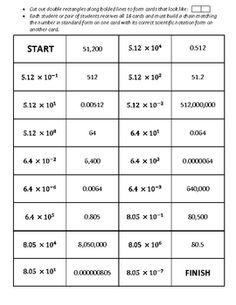
Scientific Notation Worksheet with Answer Key

Scientific notation worksheets are a valuable resource for students studying math or science. These worksheets provide practice and reinforcement when it comes to understanding and utilizing scientific notation. Whether you are a middle school student learning the basics or a high school student aiming to improve your skills, these worksheets offer an organized and structured approach to grasping this important concept.

  Scientific Notation Worksheet

---

  Significant Figures Chemistry Worksheet Answers

---

  Scientific Notation Worksheet

---

  Scientific Notation Worksheet Answers

---

  Converting Scientific Notation Worksheets

---

  Scientific Notation Worksheet

---

  Scientific Notation Worksheet Answer Key

---

  Numbers in Scientific Notation

---

What is scientific notation?

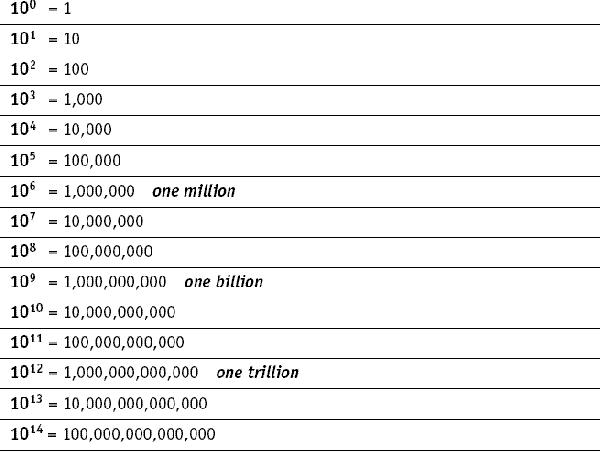
Scientific notation is a way to express very large or very small numbers in a more concise and standardized format by using powers of 10. It is written in the form of a number between 1 and 10 multiplied by a power of 10, where the power represents how many places the decimal point was moved to create the original number. This notation is particularly useful for simplifying calculations and comparing numbers across different scales in science, engineering, and mathematics.

Why is scientific notation used in scientific calculations?

Scientific notation is used in scientific calculations because it helps simplify and manage very large or very small numbers. By representing numbers as a coefficient multiplied by a power of 10, scientists can easily work with numbers across different scales without losing precision or having to write out numerous zeros. This notation makes calculations more efficient, aids in data analysis, and ensures that results are easily understood and communicated in a standardized format.

How is a number written in scientific notation?

A number in scientific notation is written with a coefficient (a number between 1 and 10) multiplied by 10 raised to a certain power. For example, the number 6,500,000 in scientific notation would be written as 6.5 x 10^6, where 6.5 is the coefficient and 6 is the exponent of 10.

How can you convert a number from scientific notation to standard notation?

To convert a number from scientific notation to standard notation, multiply the decimal part of the scientific notation by 10 raised to the power of the exponent. For example, if you have a number in scientific notation like 3.5 x 10^4, you would multiply 3.5 by 10,000 (10^4) to get the standard notation, which is 35,000.

How can you convert a number from standard notation to scientific notation?

To convert a number from standard notation to scientific notation, count the number of places you move the decimal point to the left to create a number between 1 and 10. This will be the exponent of 10 in scientific notation. The original number multiplied by 10 to the power of the number of places you moved the decimal point will give you the number in scientific notation.

What is the exponent in scientific notation and what does it represent?

The exponent in scientific notation represents the number of places the decimal point was moved to create a number between 1 and 10. It tells us how many times to multiply the base number (usually 10) by itself in order to accurately represent the original number in a more concise format.

How can you determine the number of significant figures in a number written in scientific notation?

To determine the number of significant figures in a number written in scientific notation, count all digits that are not zeros as significant figures. Zeros between non-zero digits and to the right of a decimal point are also considered significant. However, zeros to the left of the first non-zero digit are not significant. The total number of significant figures is the total count of all these digits in the number.

How can you perform addition and subtraction with numbers in scientific notation?

To perform addition and subtraction with numbers in scientific notation, you first need to ensure that the exponents of the numbers are the same. If they are not, adjust one or both of the numbers so that the exponents match. Once the exponents are aligned, you can simply add or subtract the coefficients of the numbers while keeping the same exponent. Finally, normalize the result if needed by adjusting the coefficient and the exponent to maintain scientific notation format.

How can you perform multiplication and division with numbers in scientific notation?

To multiply numbers in scientific notation, you can multiply the coefficients and add the exponents. For division, you can divide the coefficients and subtract the exponent of the divisor from the exponent of the dividend. Remember to adjust the final answer to ensure it is in proper scientific notation format, with one non-zero digit to the left of the decimal point.

How can you use scientific notation to express very large or very small numbers?

Scientific notation is used to express very large or very small numbers by writing the number as a coefficient multiplied by a power of 10. For very large numbers, the coefficient is a number between 1 and 10, and the power of 10 is positive, indicating the number of places the decimal point needs to be moved to the right. For very small numbers, the coefficient is still between 1 and 10, but the power of 10 is negative, indicating the number of places the decimal point needs to be moved to the left. This helps simplify calculations and make it easier to compare and work with numbers of vastly different magnitudes.