Scientific Notation Addition Worksheets
Scientific notation addition worksheets provide an effective and engaging way for students to practice and improve their skills in adding numbers written in scientific notation. These worksheets are designed to cater to the needs of middle and high school students who are studying or interested in science, mathematics, or any subject that requires dealing with large or small numbers.
Table of Images 👆
- Math Addition Bingo Cards
- Fifth Grade Math Worksheets
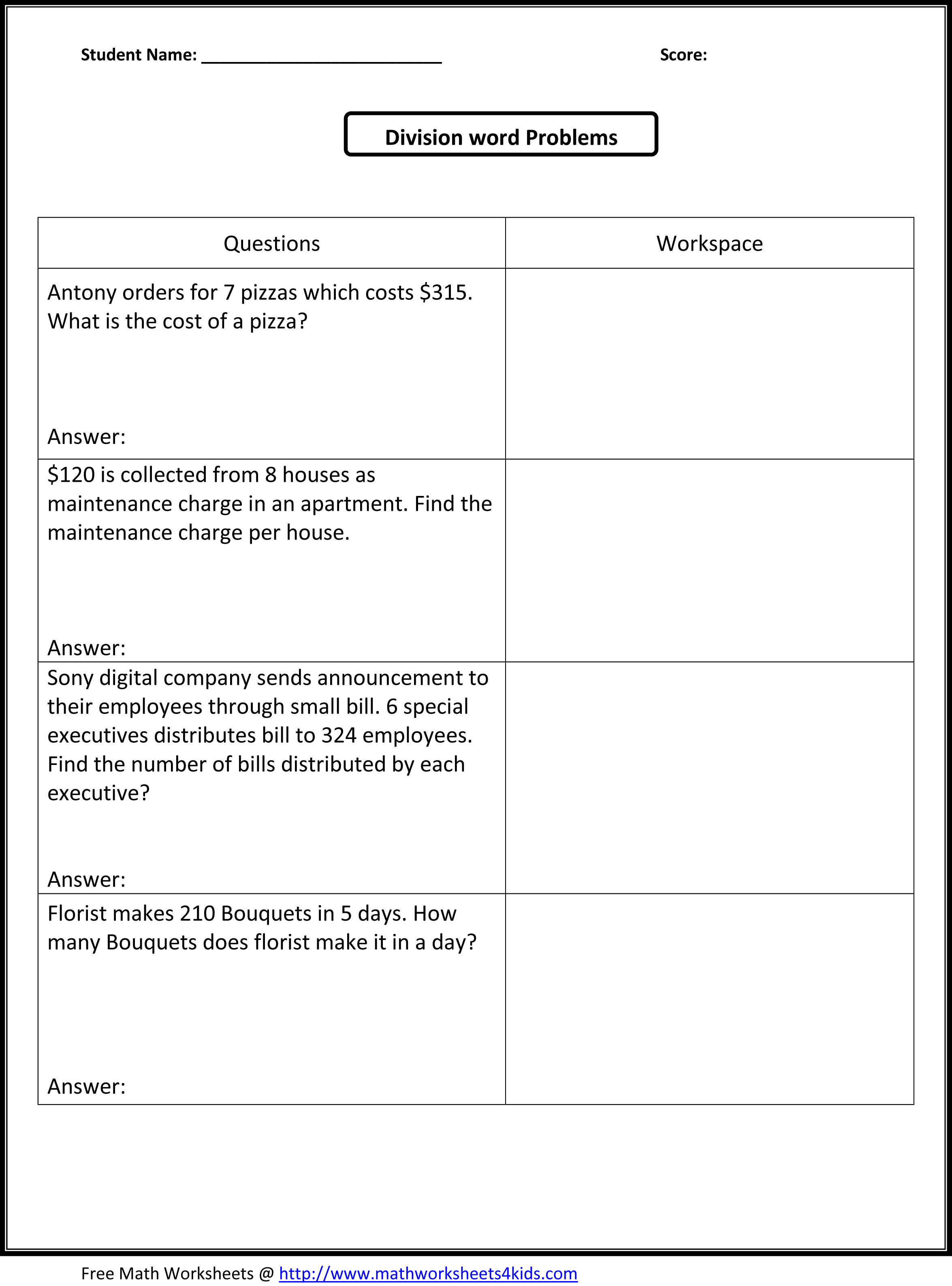
- 5th Grade Math Word Problems Worksheets
- Significant Figures Worksheet Answers
- Bedmas Math Worksheets Grade 7
- Scientific Notation Word Problems
- Exponential Notation Worksheets
- Writing Standard Form Worksheets
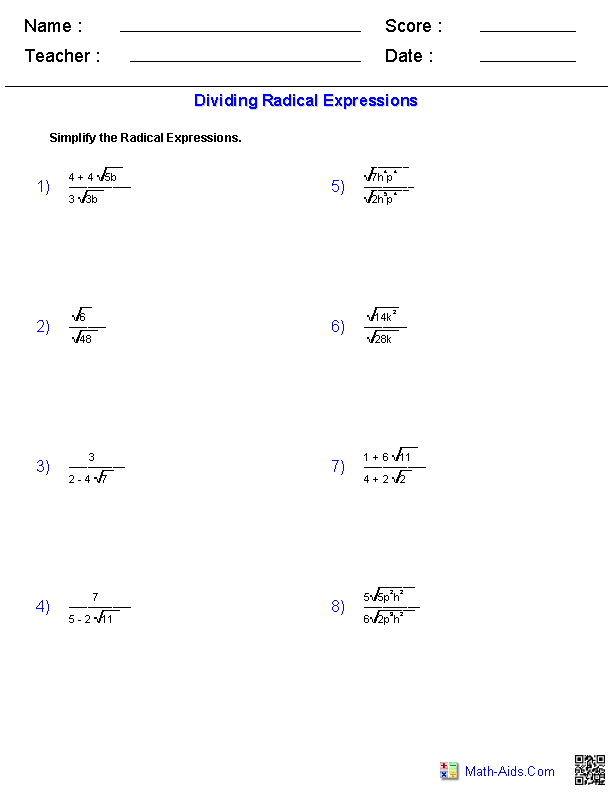
- Dividing Radical Expressions Worksheets
- Proper and Improper Fractions Worksheets
- 5th Grade Math Worksheets Printable
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
What is scientific notation?
Scientific notation is a way of writing numbers in a concise format using powers of 10. It involves writing a number as a coefficient multiplied by 10 raised to an exponent, where the coefficient is greater than or equal to 1 but less than 10, and the exponent indicates the position of the decimal point. This notation simplifies representing very large or very small numbers and facilitates calculations involving them in a more manageable way.
How is scientific notation used in expressing large numbers?
Scientific notation is used in expressing large numbers by representing them as a coefficient multiplied by 10 raised to a certain power. This allows for a more concise and easier way to write out very large numbers without having to write out all the zeros. For example, the number 5,000,000 can be written as 5 x 10^6 in scientific notation, indicating that it is 5 multiplied by 10 to the power of 6. This format is a standard way to communicate exceedingly large numbers in a more compact form.
How is scientific notation used in expressing small numbers?
Scientific notation is used to express small numbers by representing them as a decimal number between 1 and 10 multiplied by a power of 10. For example, the number 0.000027 can be written in scientific notation as 2.7 x 10^-5, where the decimal is moved to have one non-zero digit before it and the exponent indicates the number of places the decimal was moved. This helps simplify large or small numbers and make them easier to work with in calculations.
How do you add numbers in scientific notation?
To add numbers in scientific notation, first align the exponents of the two numbers. Then, add or subtract the coefficients and keep the same exponent. If needed, adjust the coefficient to ensure it is in scientific notation format, with a single non-zero digit before the decimal point and after.
How do you subtract numbers in scientific notation?
To subtract numbers in scientific notation, first ensure the exponents are the same by shifting the decimal point in one or both numbers to align the exponents. Then, subtract the coefficients while keeping the exponent the same. Lastly, convert the result back to scientific notation if necessary by adjusting the coefficient and exponent to ensure only one digit appears before the decimal point.
Can you provide an example of adding numbers in scientific notation?
Sure, here's an example: Adding 2.5 x 10^3 and 4.7 x 10^4 in scientific notation would involve making the exponents of both numbers the same, which would result in 0.25 x 10^4 + 4.7 x 10^4. Adding these together would give 4.95 x 10^4 as the final answer in scientific notation.
Can you provide an example of subtracting numbers in scientific notation?
Sure! Let's say we want to subtract 6.2 x 10^4 from 8.5 x 10^5. First, we need to make sure both numbers have the same exponent. We can do this by converting 6.2 x 10^4 to 0.062 x 10^6. Now, subtracting the two numbers gives us 8.5 x 10^5 - 0.062 x 10^6 = 8.5 x 10^5 - 6.2 x 10^5 = 2.3 x 10^5.
What are the rules for multiplying numbers in scientific notation?
To multiply numbers in scientific notation, multiply the coefficients together and add the exponents. This simplifies the calculation by combining the powers of 10 represented by the exponents. The product should then be written in scientific notation format, with the coefficient adjusted and the exponent reflecting the simplified result of the multiplication.
What are the rules for dividing numbers in scientific notation?
When dividing numbers in scientific notation, you divide the coefficients and then subtract the exponents of the 10 base. For example, when dividing 5 x 10^4 by 2 x 10^2, you would compute 5 ÷ 2 = 2.5 and then subtract the exponents to get 10^(4-2) = 10^2. Thus, the result would be 2.5 x 10^2.
Can you provide an example of multiplying and dividing numbers in scientific notation?
Sure! Let's multiply 3.5 x 10^5 by 2 x 10^4. First, multiply the coefficients: 3.5 x 2 = 7. Then, add the exponents: 5 + 4 = 9. Therefore, the result is 7 x 10^9. Now, let's divide 7.2 x 10^8 by 3 x 10^3. Dividing the coefficients 7.2 ÷ 3 = 2.4 and subtracting the exponents gives 10^8 ÷ 10^3 = 10^5. Thus, the answer is 2.4 x 10^5.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.







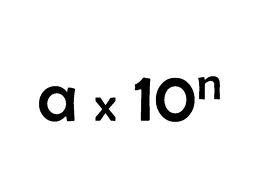


















Comments