Right Angle Trigonometry Worksheet

Are you struggling to find a reliable resource for right angle trigonometry worksheets? Look no further, as we have exactly what you need! Our comprehensive collection of right angle trigonometry worksheets is perfect for students who are seeking to strengthen their understanding of this important mathematical concept. Whether you are a teacher searching for classroom materials or a student aiming to improve your skills, our worksheets provide a structured and engaging way to practice and master right angle trigonometry.

  Right Triangle Trig Word Problems Worksheet

---

  Non Right Triangle Trigonometry

---

  Special Right Triangles Worksheet Answers

---

  Right Triangle Trigonometry Worksheet

---

  Euler Formula Complex Exponentials

---

  Overlapping Triangle Proofs Worksheet

---

  Trig Tables Sin Cos Tan

---

What is the definition of a right angle?

A right angle is a 90-degree angle formed by two perpendicular lines intersecting, creating two equal angles of 45 degrees each.

How many degrees are in a right angle?

There are 90 degrees in a right angle.

In a right triangle, where is the right angle located?

The right angle in a right triangle is located at the intersection of the two shorter sides, known as the legs, forming a 90-degree angle.

What is the relationship between the lengths of the sides in a right triangle?

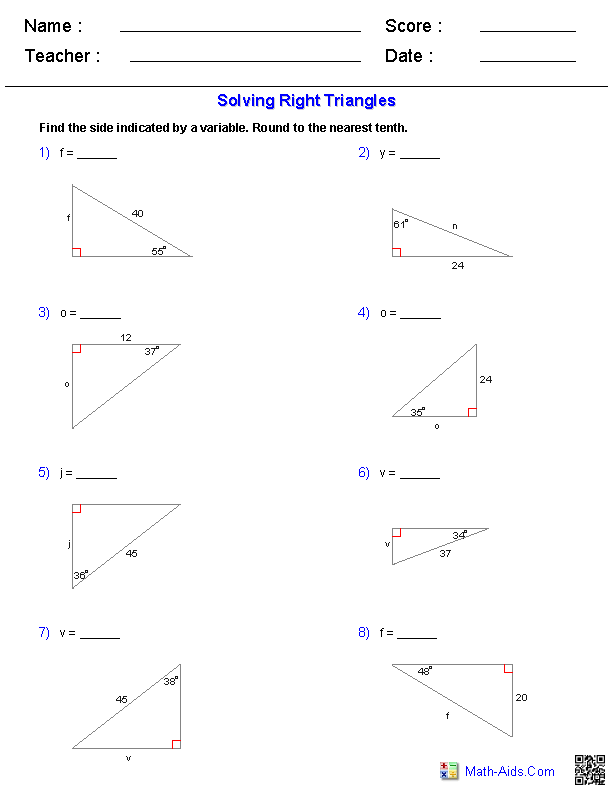
In a right triangle, the relationship between the lengths of the sides is governed by the Pythagorean theorem, which states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This relationship enables us to calculate the lengths of sides based on the lengths of the other sides in a right triangle.

What is the Pythagorean Theorem and how is it used in right angle trigonometry?

The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, it is expressed as a^2 + b^2 = c^2, where 'c' is the length of the hypotenuse, and 'a' and 'b' are the lengths of the other two sides. In right angle trigonometry, the Pythagorean Theorem is a fundamental principle used to find the length of a side in a right-angled triangle when the lengths of the other two sides are known, thus enabling the calculation of trigonometric functions such as sine, cosine, and tangent.

What are the trigonometric ratios for sine, cosine, and tangent?

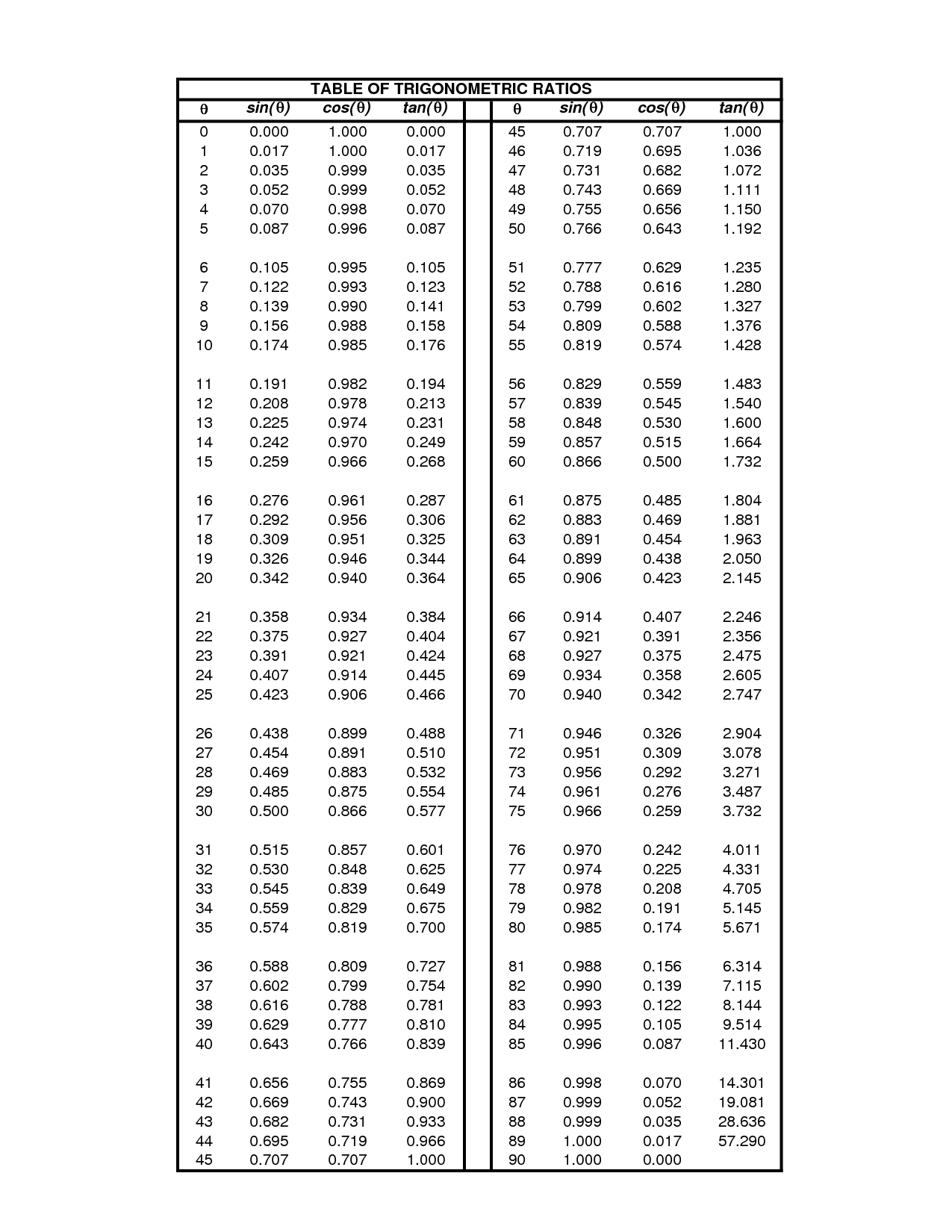
The trigonometric ratios for sine, cosine, and tangent are basic functions used in trigonometry to relate the angles of a right triangle to the lengths of its sides. Sine (sin) is equal to the length of the side opposite an angle divided by the hypotenuse, cosine (cos) is the length of the adjacent side divided by the hypotenuse, and tangent (tan) is the length of the opposite side divided by the adjacent side.

How are the trigonometric ratios calculated using the sides of a right triangle?

Trigonometric ratios are calculated using the sides of a right triangle by comparing the lengths of the sides to each other. The most common trigonometric ratios are sine, cosine, and tangent, which are calculated as follows: sine = opposite/hypotenuse, cosine = adjacent/hypotenuse, and tangent = opposite/adjacent. By dividing the lengths of the sides in these specific ways, we can determine the relationships between the angles and sides of a right triangle.

What is the reciprocal of sine, cosine, and tangent? How are they calculated?

The reciprocal of sine is cosecant, which is calculated as 1/sin(x). The reciprocal of cosine is secant, calculated as 1/cos(x). The reciprocal of tangent is cotangent, calculated as 1/tan(x). These reciprocals are found by taking the multiplicative inverse of the corresponding trigonometric function.

What are the inverse trigonometric functions and how are they used in right angle trigonometry?

The inverse trigonometric functions are functions that undo the trigonometric functions. They are denoted as arcsin, arccos, arctan, etc., and they are used to find an angle given the ratio of sides in a right triangle. In right angle trigonometry, these functions help in solving for angles in a triangle when given the lengths of at least two sides. They essentially allow us to find the angles that correspond to specific trigonometric ratios, such as sine, cosine, and tangent, which can be useful in various real-world applications involving geometry or physics.

How can right angle trigonometry be applied in real-world scenarios?

Right angle trigonometry can be applied in various real-world scenarios such as in architecture for designing buildings, in engineering for constructing bridges and roads, in astronomy for calculating distances between celestial bodies, in navigation for determining position and direction, in physics for analyzing forces and motion, and in computer graphics for creating realistic 3D models. By using trigonometric functions like sine, cosine, and tangent, measurements of angles and lengths can be accurately calculated to solve practical problems in different fields.