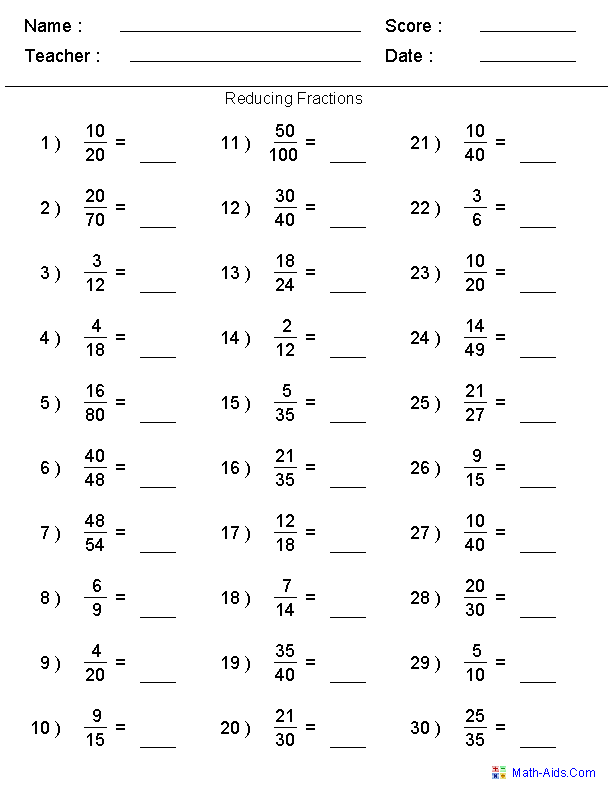
Reducing Fractions Worksheets 6th Grade

Are you searching for a valuable tool to help your 6th-grade students strengthen their skills in reducing fractions? Look no further, as we have the perfect solution for you - worksheets! Worksheets are an effective way to engage students and provide them with hands-on practice in reducing fractions. With carefully designed exercises, these worksheets will enhance your students' understanding of this essential math concept while keeping them actively involved in the learning process.

  Reducing Fractions Worksheet 5th Grade

---

  6th Grade Math Worksheets Fractions

---

  6th Grade Math Worksheets Fractions

---

  6th Grade Math Worksheets Fractions

---

  Fractions Worksheets Grade 6

---

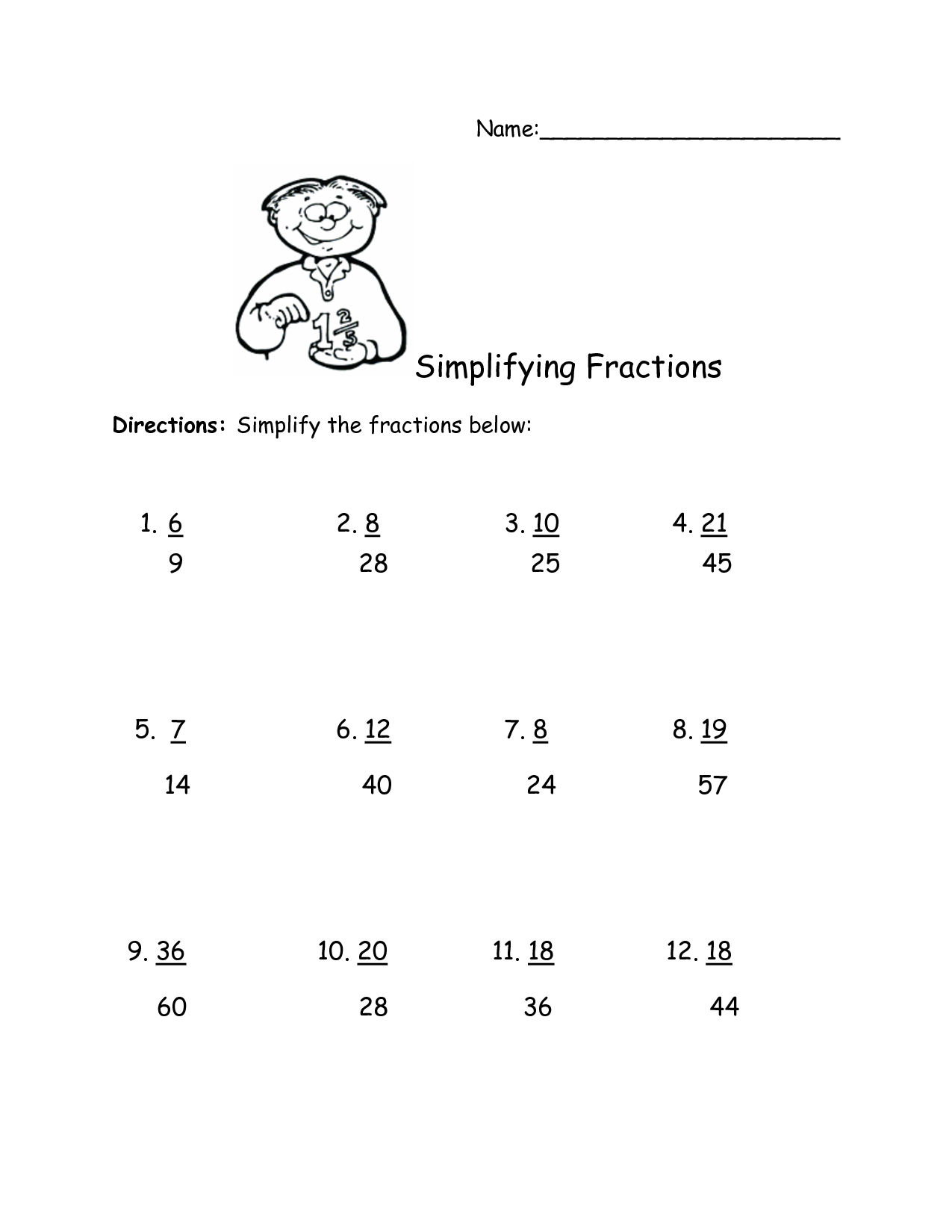
  Simplifying Fractions Worksheet

---

  4th Grade Printable Math Worksheets Fractions

---

  Improper Fractions Worksheets

---

  Equivalent Fractions Worksheets 6th Grade

---

  Adding Fractions 6th Grade Math Worksheets

---

  Simplifying Fractions Worksheet

---

  Simplifying Fractions Worksheets 5th Grade Math

---

  Reducing Fractions Worksheet Lowest Terms

---

  Equivalent Fractions Worksheets 6th Grade Math

---

  Simplifying Fractions Worksheet

---

  Equivalent Fractions Worksheet

---

  Simplifying Fractions Worksheet

---

  5th Grade Math Worksheets Fractions

---

What is a fraction?

A fraction is a numerical quantity that represents a part or parts of a whole. It consists of a numerator (the top number) which represents the number of parts being considered, and a denominator (the bottom number) which represents the total number of equal parts that make up the whole. Fractions are used to express values that are not whole numbers, allowing us to describe quantities that are not integers.

What is a reducing fraction?

A reducing fraction is a fraction where the numerator and denominator have no common factors greater than 1. To reduce a fraction means to simplify it by dividing both the numerator and the denominator by their greatest common factor, resulting in an equivalent fraction with smaller or simpler numbers.

How do you find the greatest common factor (GCF) of a fraction?

To find the greatest common factor (GCF) of a fraction, you first need to break down the numerator and denominator of the fraction into their prime factors. Then, identify the common prime factors between the numerator and denominator and multiply them together to get the GCF. Finally, divide both the numerator and denominator of the fraction by the GCF to simplify the fraction.

How do you determine if a fraction is already reduced?

To determine if a fraction is already reduced, you need to find the greatest common factor (GCF) of the numerator and the denominator. If the GCF is 1, then the fraction is already in its simplest form and cannot be further reduced. If the GCF is greater than 1, then the fraction can be simplified further by dividing both the numerator and denominator by the GCF to get the reduced form.

How do you simplify a fraction by reducing it?

To simplify a fraction by reducing it, you need to find the greatest common divisor (GCD) of the numerator and denominator, and then divide both by this value. This will yield the simplest form of the fraction. Keep dividing by the GCD until the numerator and denominator no longer have any common factors. This process will result in the fraction being reduced to its simplest form.

Can all fractions be reduced to their simplest form?

Yes, all fractions can be reduced to their simplest form by dividing both the numerator and denominator by their greatest common divisor until they are no longer divisible by any common factor other than 1. This process simplifies the fraction to its lowest terms, ensuring that it is expressed with the smallest possible whole number values in the numerator and denominator.

What is the benefit of reducing fractions?

Reducing fractions has the benefit of simplifying and making the fraction easier to work with or understand. By reducing fractions to their simplest form, you can more easily compare, add, subtract, multiply, or divide them. It also helps in visualizing and grasping the concept of fractional parts in a clearer manner.

Are there any special rules or techniques for reducing fractions with larger numbers?

When reducing fractions with larger numbers, you can follow the same basic rules and techniques used for reducing fractions with smaller numbers. First, find the greatest common divisor (GCD) of the numerator and denominator, then divide both the numerator and denominator by this GCD to simplify the fraction. It may be helpful to break down larger numbers into their prime factors to easily identify the GCD. Additionally, if the numbers are very large, using a calculator or an online tool to find the GCD and simplify the fraction can be a time-saving approach.

What are some common mistakes students make when reducing fractions?

Common mistakes students make when reducing fractions include not simplifying by dividing the numerator and denominator by their greatest common factor, trying to cancel out individual digits instead of the entire numbers, forgetting negative signs, and not minimizing fractions in their simplest form. It's important for students to remember to simplify fractions by dividing both the numerator and the denominator by the greatest common factor to accurately reduce them.

Can you provide an example of a reducing fractions worksheet question with step-by-step solution?

Example of a reducing fractions worksheet question: Simplify the fraction 16/24. Step-by-step solution: To reduce the fraction 16/24, we first find the greatest common divisor (GCD) of 16 and 24, which is 8. Then, we divide both the numerator and the denominator by 8 to simplify the fraction: 16 ÷ 8 = 2 and 24 ÷ 8 = 3. Therefore, the fraction 16/24 simplifies to 2/3.