Reducing Fractions Worksheet Printable

Are you searching for a helpful tool to reinforce your understanding of reducing fractions? Look no further! We have created a printable worksheet that focuses specifically on this topic. Designed for students in grades 4-6, this worksheet is perfect for practicing and improving skills in reducing fractions to their simplest form.

  Reducing Fractions Worksheet Lowest Terms

---

  Simplifying Fractions Worksheet

---

  3rd Grade Math Worksheets Fractions

---

  Reducing Fractions Worksheet Answers

---

  Fractions Math Aids Worksheets Answers

---

  Mixed Fractions Worksheets

---

  Multiplication Worksheets 100 Problems

---

  Adding 3 Fractions Worksheets

---

  4th Grade Math Worksheets Fractions

---

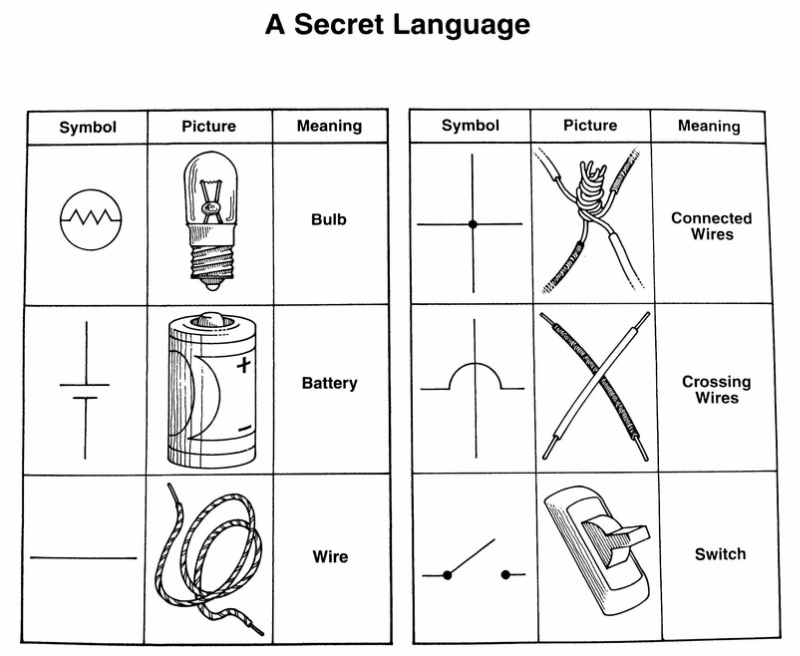
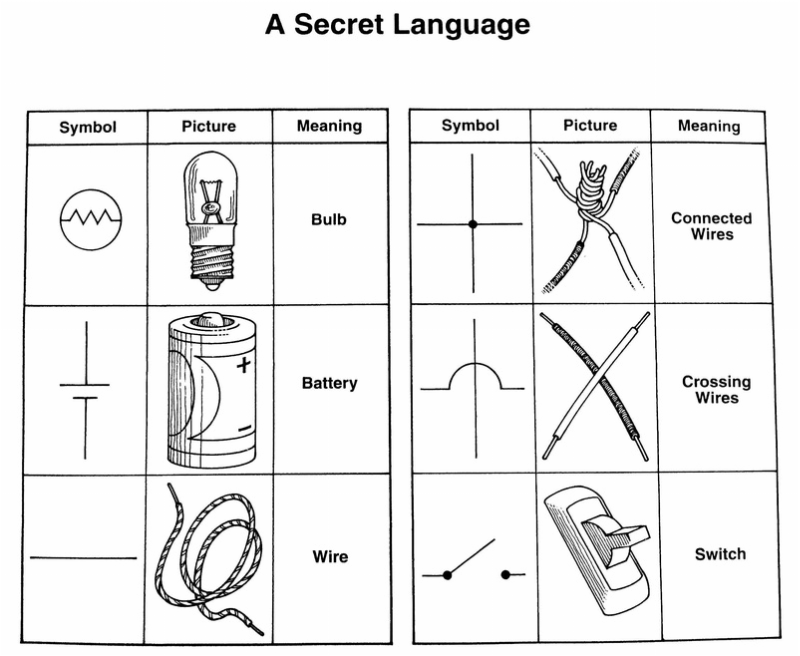
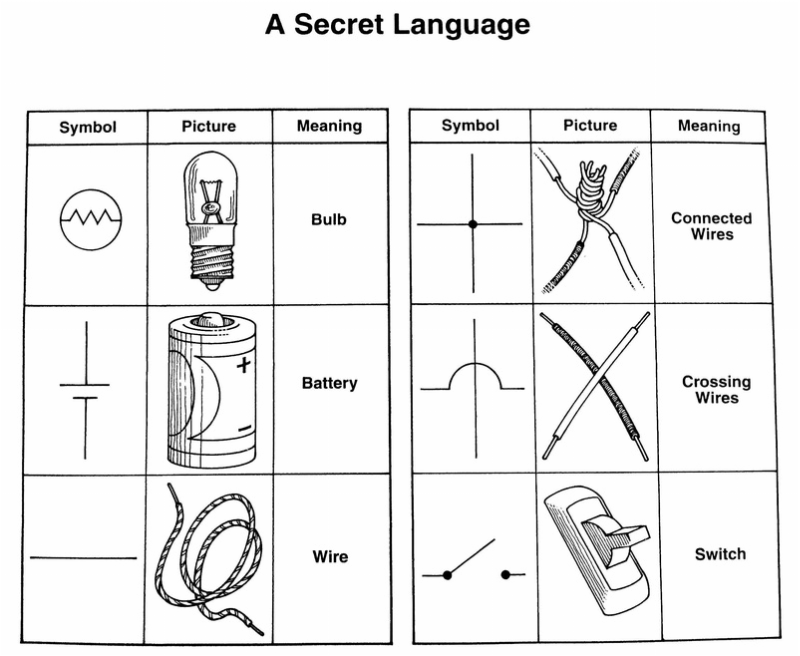
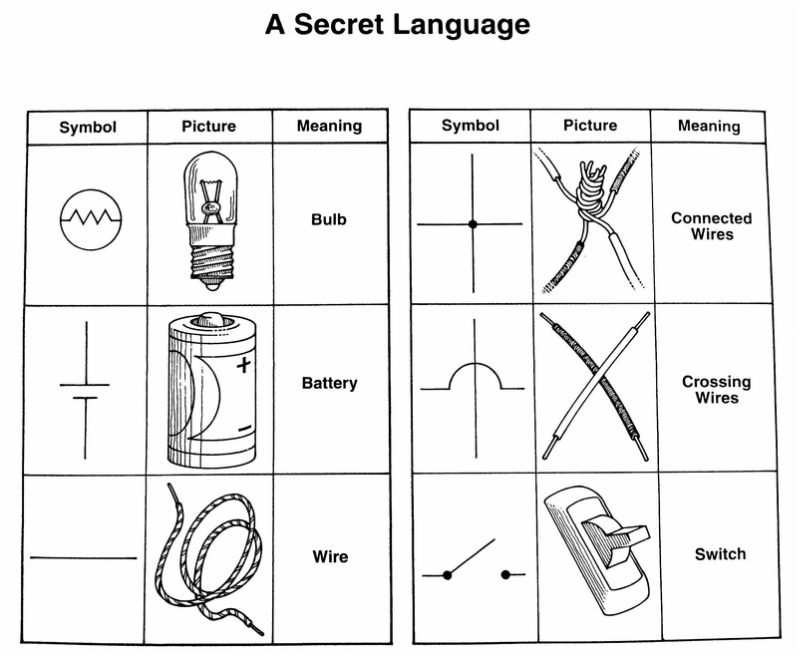
  Electricity Circuit Worksheets 4th Grade

---

  Electricity Circuit Worksheets 4th Grade

---

  Electricity Circuit Worksheets 4th Grade

---

  Electricity Circuit Worksheets 4th Grade

---

What is a reducing fraction?

A reducing fraction is a fraction where the numerator and denominator have no common factors other than 1, resulting in the fraction being in its simplest form. This is achieved by dividing both the numerator and denominator by their greatest common factor until no further simplification is possible.

How do you find the greatest common divisor of a fraction?

To find the greatest common divisor of a fraction, you need to determine the highest number that can evenly divide both the numerator and the denominator of the fraction. Once you have identified the factors of both numbers, you can then find the greatest common divisor by identifying the largest number that is common to both sets of factors. This will give you the greatest common divisor of the fraction.

Why is it important to reduce fractions?

Reducing fractions is important because it helps simplify and clarify numerical relationships. By reducing a fraction to its simplest form, we make it easier to compare fractions, add or subtract them, or perform other mathematical operations. Additionally, reduced fractions can provide a clearer representation of the original quantity or proportion, making them more practical and easier to work with in various mathematical contexts.

What is the process of reducing a fraction?

To reduce a fraction, you find the greatest common divisor (GCD) of the numerator and denominator, and then divide both the numerator and denominator by this common divisor. By simplifying the fraction in this way, you can express it in its lowest terms, making it easier to work with and understand.

Can all fractions be reduced to their simplest form?

Not all fractions can be reduced to their simplest form. Some fractions are already in their simplest form, also known as being in lowest terms. These fractions have no common factors between the numerator and the denominator that can be divided out further. For example, 3/7 is already in its simplest form because 3 and 7 do not share any common factors other than 1.

How do you simplify fractions using prime factorization?

To simplify fractions using prime factorization, you need to find the prime factorization of both the numerator and the denominator. Then, identify common factors between the numerator and denominator and divide them out. Continue this process until there are no common factors left, resulting in the simplified fraction. This method helps in simplifying fractions efficiently by breaking down the numbers into their prime factors and canceling out the common factors.

What is the difference between a proper fraction and an improper fraction?

A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number), resulting in a value less than 1. On the other hand, an improper fraction is a fraction where the numerator is equal to or larger than the denominator, resulting in a value equal to or greater than 1.

Are there any rules or techniques for determining when a fraction can be simplified?

Yes, there are rules and techniques for determining when a fraction can be simplified. One common technique is to find the greatest common factor (GCF) of the numerator and denominator and then divide both by this factor. A fraction can also be simplified if both the numerator and denominator have a common factor other than 1. Additionally, fractions can be simplified by converting them to their simplest form, such as reducing improper fractions or mixed numbers. Ultimately, simplifying fractions involves reducing them to their lowest terms by dividing both the numerator and denominator by their greatest common factor.

How can reducing fractions be helpful in real-life situations?

Reducing fractions can be helpful in real-life situations because it simplifies and clarifies quantities. For example, when working with measurements or recipes, reducing fractions can help ensure accuracy and precision. In financial situations, such as when calculating interest rates or discounts, reducing fractions can make calculations more manageable and easier to compare values. Overall, reducing fractions can save time, prevent errors, and provide a clearer understanding of proportions in various practical applications.

Are there any shortcuts or tips for quickly reducing fractions?

One useful shortcut for quickly reducing fractions is to look for common factors between the numerator and denominator, and then divide both numbers by the greatest common factor (GCF) until the fraction is in its simplest form. It can also be helpful to memorize common fractions and their decimal equivalents, as well as using a fraction calculator for more complex fractions to quickly find the simplest form.