Rectangular Prism Volume Worksheet

Are you in search of a practical and informative worksheet to help your middle school students understand and calculate the volume of rectangular prisms? Look no further! This volume worksheet provides a comprehensive overview of finding the volume of rectangular prisms and is designed to engage students as they develop their skills in this mathematical concept. With clear instructions and a variety of practice problems, this worksheet is perfect for educators seeking to reinforce the concept of volume with their students.

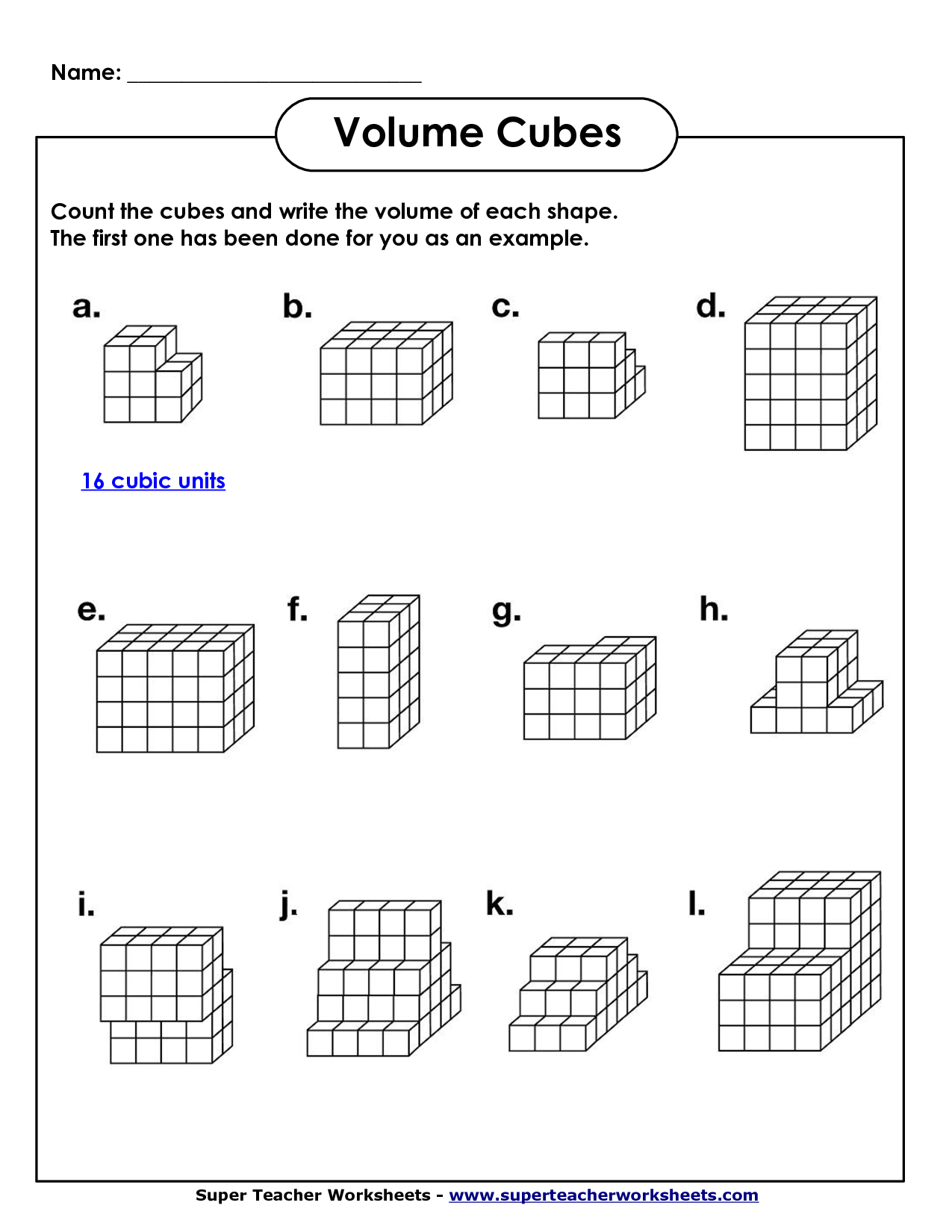
  Cube Volume Worksheets 5th Grade Math

---

  Surface Area and Volume Worksheets Grade 6

---

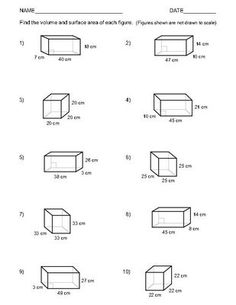
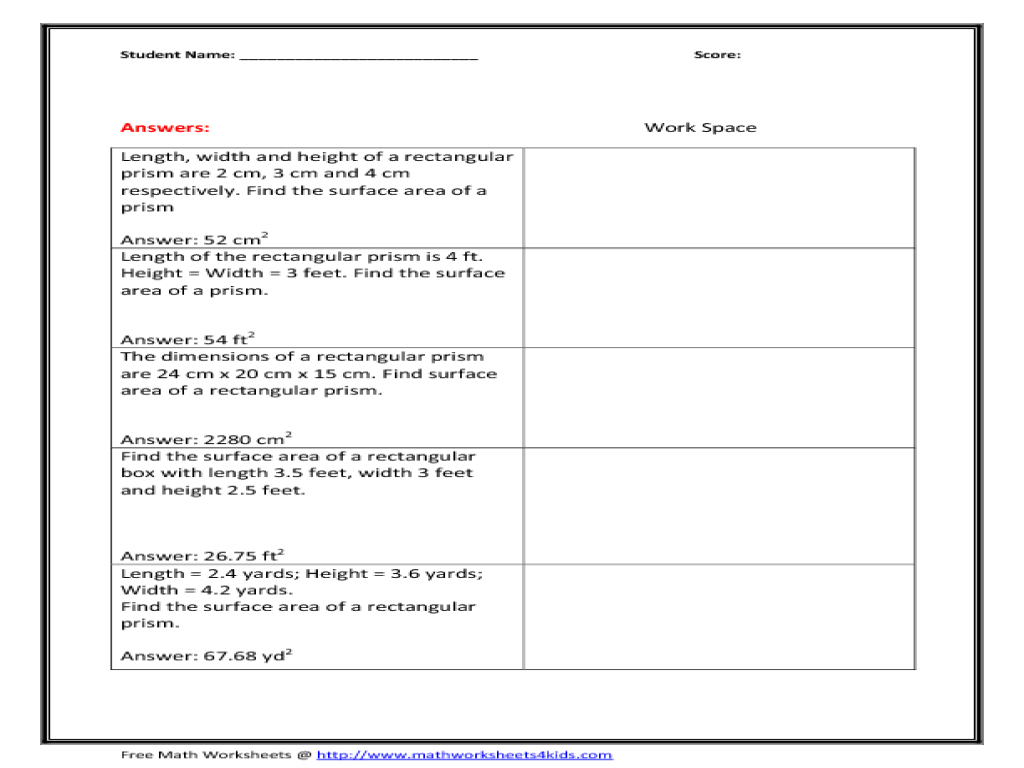
  Surface Area Rectangular Prism Volume Worksheet

---

  Rectangular Prism Surface Area Worksheet

---

  Surface Area Rectangular Prism Volume

---

  Surface Area and Volume Worksheets

---

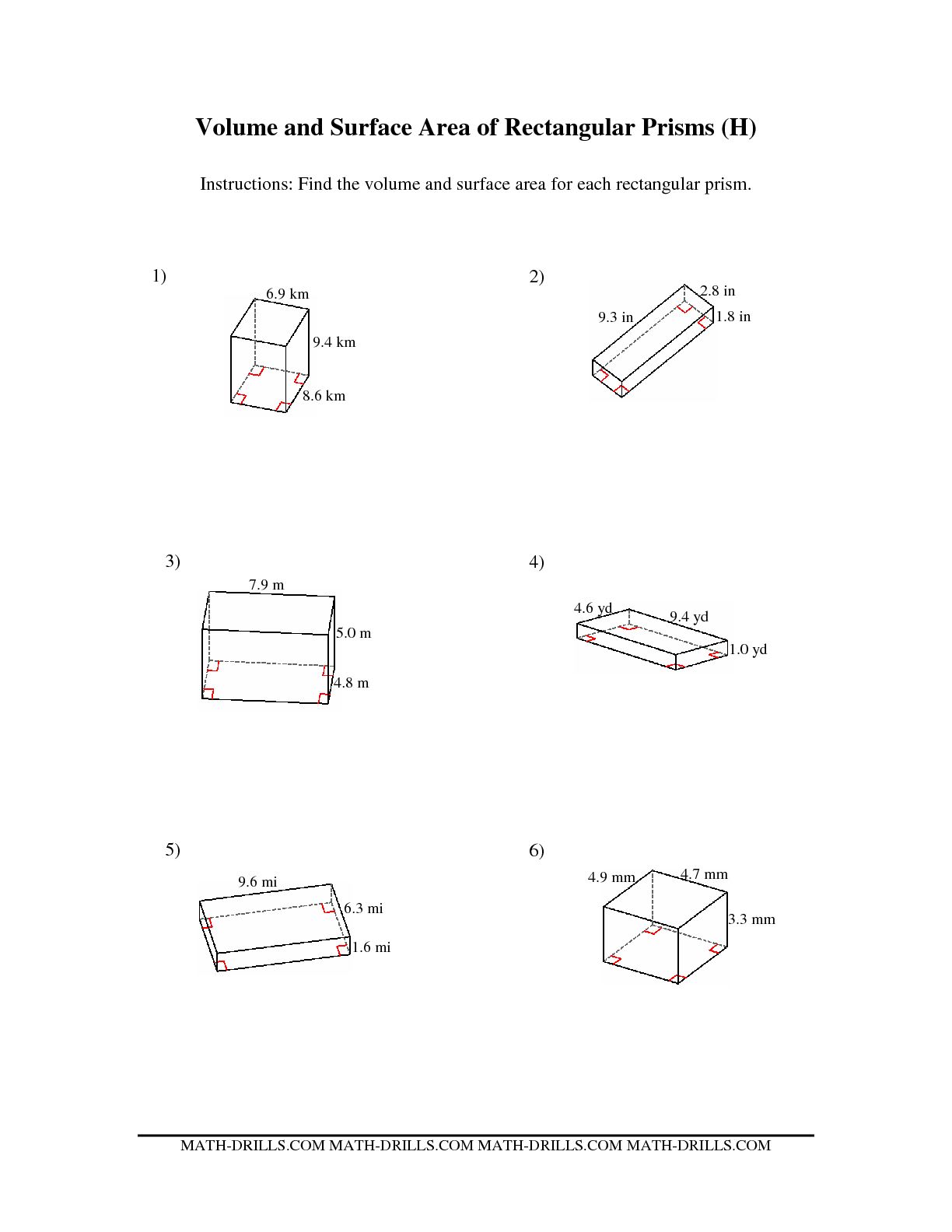
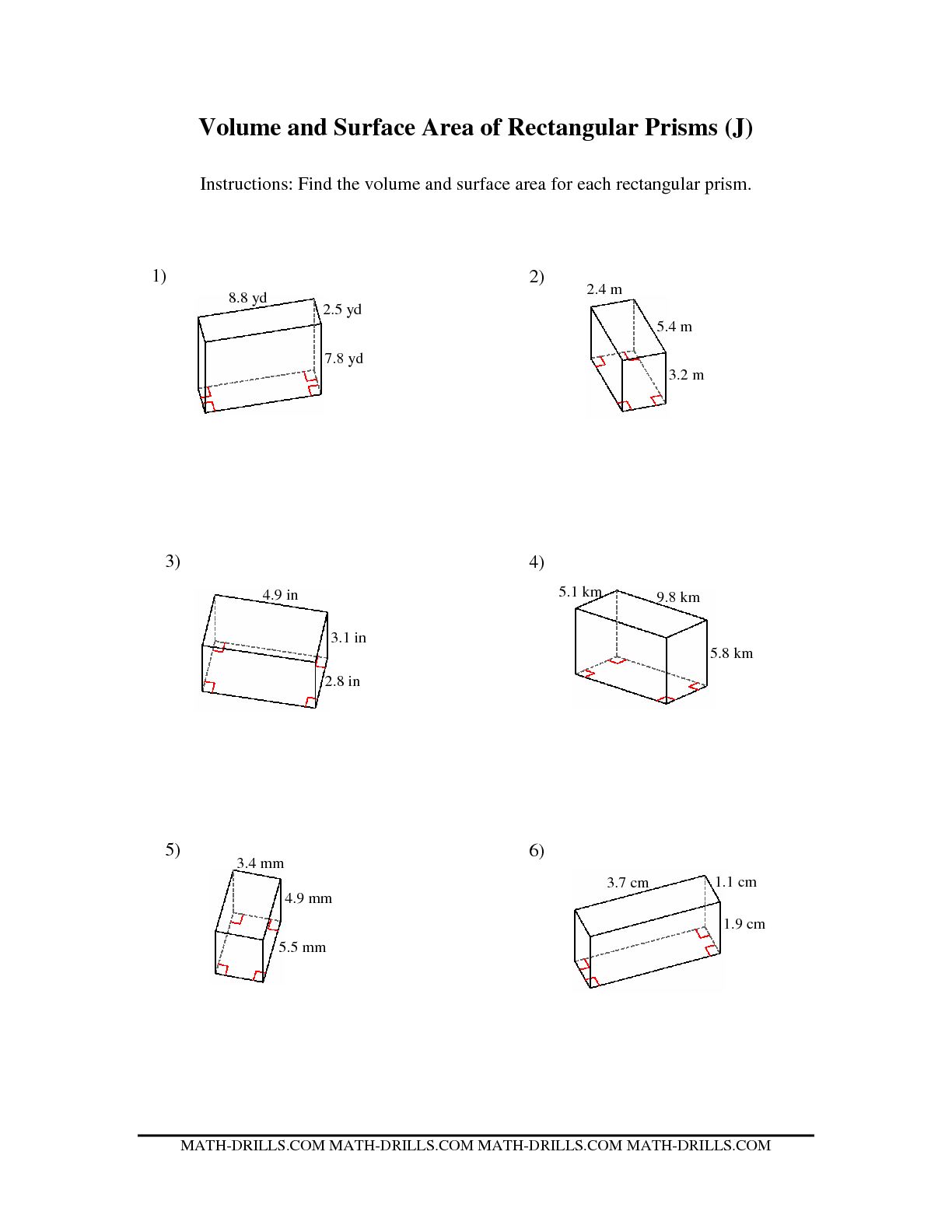
  Surface Area Rectangular Prism Volume Worksheet

---

  Surface Area of Rectangular Prism

---

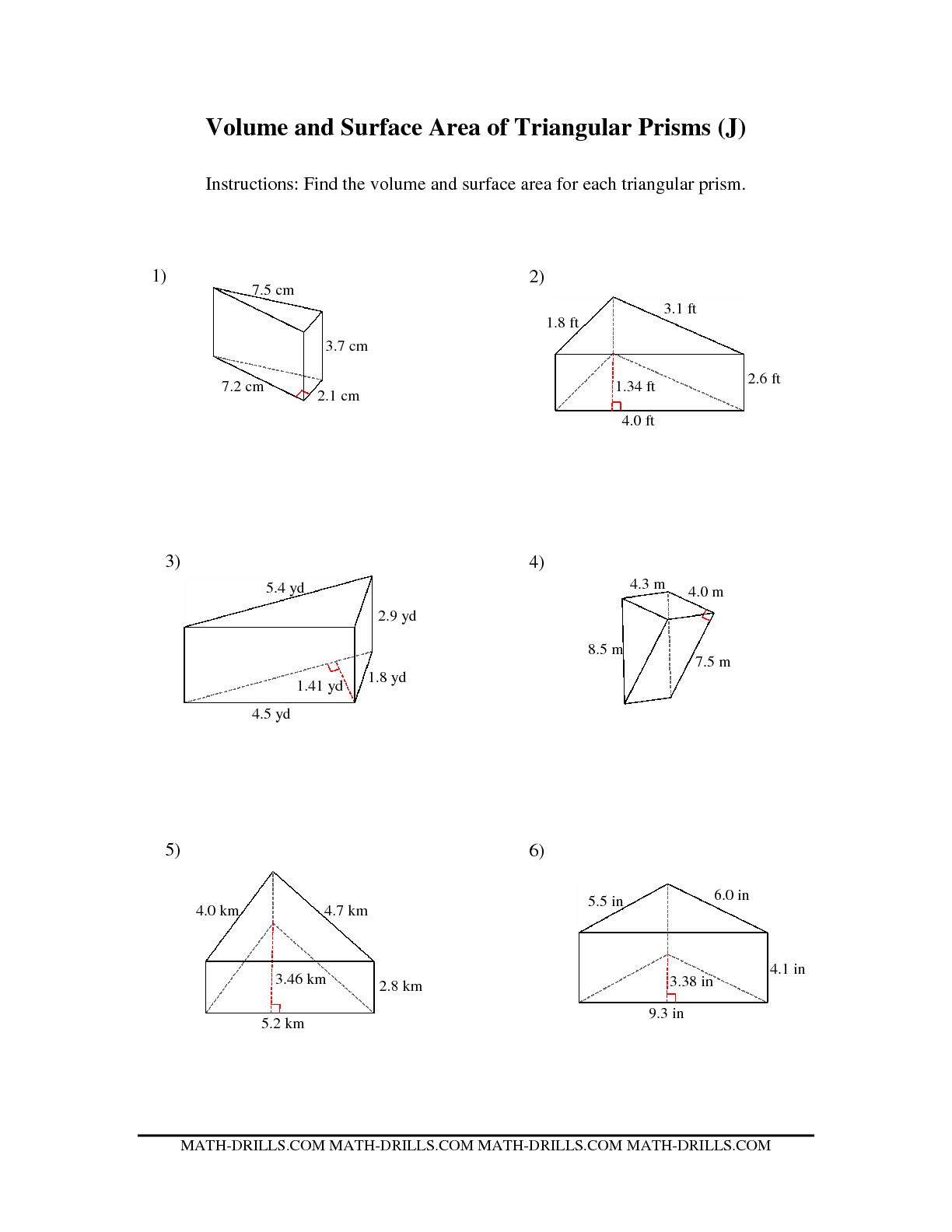
  Triangular Prism Surface Area Worksheet

---

  Find Surface Area Triangular Prism

---

  90 Degrees Counterclockwise

---

  Triangular Prism Surface Area Worksheet

---

  Triangular Prism Surface Area Worksheet

---

  Triangular Prism Surface Area Worksheet

---

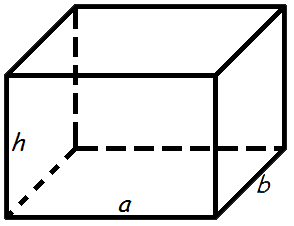
What is the formula for finding the volume of a rectangular prism?

The formula for finding the volume of a rectangular prism is V = l x w x h, where V represents the volume, l represents the length, w represents the width, and h represents the height of the rectangular prism.

What are the units used to measure volume?

The units used to measure volume are liters (L) and milliliters (mL) in the metric system, and cubic centimeters (cm^3) and cubic meters (m^3) in the international system of units.

If the length of a rectangular prism is 5 cm, the width is 3 cm, and the height is 10 cm, what is the volume?

The volume of the rectangular prism is calculated by multiplying its length, width, and height. Therefore, for these dimensions, the volume of the rectangular prism would be 5 cm x 3 cm x 10 cm = 150 cubic cm.

Can the volume of a rectangular prism be negative? Why or why not?

No, the volume of a rectangular prism cannot be negative. Volume is a measure of how much space an object occupies, and it is always a positive value because it represents a quantity of three-dimensional space. A negative volume would imply that the object has a negative amount of space, which is not logically possible in the physical world.

How does the volume change if the dimensions of a rectangular prism are doubled?

If the dimensions of a rectangular prism are doubled, the volume increases by a factor of 8. This is because volume is calculated by multiplying the length, width, and height of the prism. When all three dimensions are doubled, the new volume is 2 x 2 x 2 = 8 times larger than the original volume.

How does the volume change if the height of a rectangular prism is halved?

If the height of a rectangular prism is halved, the volume of the prism would also be halved. This is because the volume of a rectangular prism is calculated by multiplying its length, width, and height, so reducing the height by half would result in half the original volume.

What is the volume of a rectangular prism with a length of 8 inches, a width of 6 inches, and a height of 4 inches?

The volume of a rectangular prism is calculated by multiplying its length, width, and height. In this case, the volume of the rectangular prism with a length of 8 inches, a width of 6 inches, and a height of 4 inches would be 8 inches x 6 inches x 4 inches = 192 cubic inches.

If the volume of a rectangular prism is 150 cubic meters and the height is 10 meters, what are the possible dimensions for the length and width?

The length and width of the rectangular prism must multiply to give 15 cubic meters (150 cubic meters divided by the height of 10 meters). The possible dimensions could be 5 meters in length and 3 meters in width, or 3 meters in length and 5 meters in width, as both combinations would result in a volume of 150 cubic meters when multiplied by the height of 10 meters.

How does the volume of a rectangular prism compare to the volume of a cube with the same edge length?

The volume of a rectangular prism is greater than the volume of a cube with the same edge length because a rectangular prism has different lengths, widths, and heights, increasing the amount of space it occupies within its shape compared to a cube where all sides are equal. This means that a rectangular prism has a larger volume due to its elongated shape, even though both the prism and the cube share the same edge length.

Explain how you can use the volume of a rectangular prism to calculate the amount of liquid it can hold.

To calculate the amount of liquid a rectangular prism can hold, you can use the formula for volume, which is length x width x height. This formula will give you the total amount of space inside the prism in cubic units. So, by finding the volume of the rectangular prism, you can determine the maximum amount of liquid it can hold without overflowing.