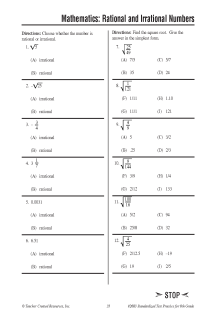
Rational and Irrational Numbers Worksheet
Are you a math teacher searching for a comprehensive worksheet to help your students practice distinguishing between rational and irrational numbers? Look no further! In this blog post, we will introduce you to a top-quality rational and irrational numbers worksheet that focuses on developing students' understanding of this important mathematical concept. With a well-structured layout and carefully crafted questions, this worksheet is designed to engage and challenge your students while ensuring they grasp the core concepts of rational and irrational numbers.
Table of Images 👆
Rational and Irrational Numbers Examples
Rational and Irrational Numbers 8th Grade Worksheets
Rational and Irrational Numbers Examples
Ordering Numbers Worksheets
Math 8 Rational Irrational Numbers Worksheet
3 Grade Math Worksheets
Rational Numbers Worksheets
Real Rational Irrational Numbers Worksheet
More Number Worksheets
Hundreds Chart Missing Numbers WorksheetTeen Number Practice Worksheet
Rational Numbers 7th Grade Math Worksheets
Number Cut Out Worksheet
Before and After Numbers Worksheets Grade 1
Missing Number Worksheets 1- 20
Kindergarten Number Worksheets 1 50
Thanksgiving Number Worksheets
What is a rational number?
A rational number is a number that can be expressed as the quotient or fraction of two integers, where the denominator is not equal to zero. In other words, any number that can be represented as a simple fraction is considered a rational number.
Provide an example of a rational number and explain why it fits the definition.
One example of a rational number is 3/4. This number fits the definition of a rational number because it can be expressed as a fraction of two integers, where the denominator is not zero. In this case, the numerator is 3 and the denominator is 4, both of which are integers. This demonstrates that 3/4 is a rational number because it can be represented as a ratio of two integers.
What is an irrational number?
An irrational number is a real number that cannot be expressed as a ratio of two integers. In simpler terms, irrational numbers are non-repeating and non-terminating decimal numbers that cannot be written in the form of a fraction. Examples of irrational numbers include ? (pi), ?2 (square root of 2), and e (Euler's number).
Give an example of an irrational number and explain why it is considered irrational.
One example of an irrational number is the square root of 2 (?2). This number is considered irrational because it cannot be expressed as a simple fraction of two integers. In other words, there is no ratio of two integers that can represent ?2 exactly. Its decimal representation goes on infinitely without repeating, making it impossible to write it as a finite or repeating decimal.
How can you determine if a number is rational or irrational?
A number is rational if it can be expressed as the ratio of two integers. In other words, a number is rational if it can be written in the form a/b, where "a" and "b" are integers and "b" is not equal to zero. On the other hand, a number is irrational if it cannot be expressed as the ratio of two integers, meaning it cannot be written in the form a/b where "a" and "b" are integers. The key difference is that rational numbers have a finite or repeating decimal representation, while irrational numbers have non-repeating and non-terminating decimal representations.
Can a number be both rational and irrational? Explain.
No, a number cannot be both rational and irrational at the same time. A rational number can be expressed as a ratio of two integers, while an irrational number cannot be expressed as a ratio of two integers and has non-repeating, non-terminating decimal representations. Since a number cannot simultaneously have a rational and an irrational representation, it cannot be both rational and irrational at the same time.
Are all natural numbers rational?
Yes, all natural numbers are rational. Rational numbers are numbers that can be expressed as a ratio of two integers, and since natural numbers are also integers, they can be represented as a ratio where the denominator is 1. Therefore, all natural numbers can be written as a fraction and are considered rational numbers.
Are all integers rational?
Yes, all integers are rational numbers because they can be expressed as a fraction where the denominator is 1. In other words, any integer can be written in the form a/1, where 'a' is the integer itself. Since rational numbers are defined as numbers that can be expressed as a ratio of two integers, integers are a subset of rational numbers.
Are all fractions rational?
Yes, all fractions are rational numbers because a fraction can always be expressed as a ratio of two integers, where the denominator is not equal to zero. Rational numbers include integers and fractions, where the denominator is not zero.
Can you find a real-life example of a rational and irrational number?
Yes, a real-life example of a rational number would be the price of gasoline at a gas station, where it can be expressed as a fraction such as $2.50 per gallon. An irrational number can be found in the value of pi when calculating the circumference of a circle, as it is a non-repeating and non-terminating decimal approximately equal to 3.14159.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
Comments