Ratio Worksheets Grade 6

Ratio worksheets are a valuable tool for grade 6 students to practice and reinforce their understanding of ratios and proportions. With a focus on the entity and subject, these worksheets provide students with a range of problems that require them to analyze and compare different quantities. Through these exercises, students can develop their mathematical skills and gain confidence in solving ratio problems independently.

  6th Grade Math Ratio Worksheets

---

  6th Grade Math Ratio Worksheets

---

  6th Grade Ratio and Unit Rate Worksheet

---

  6th Grade Ratio Word Problems Worksheets

---

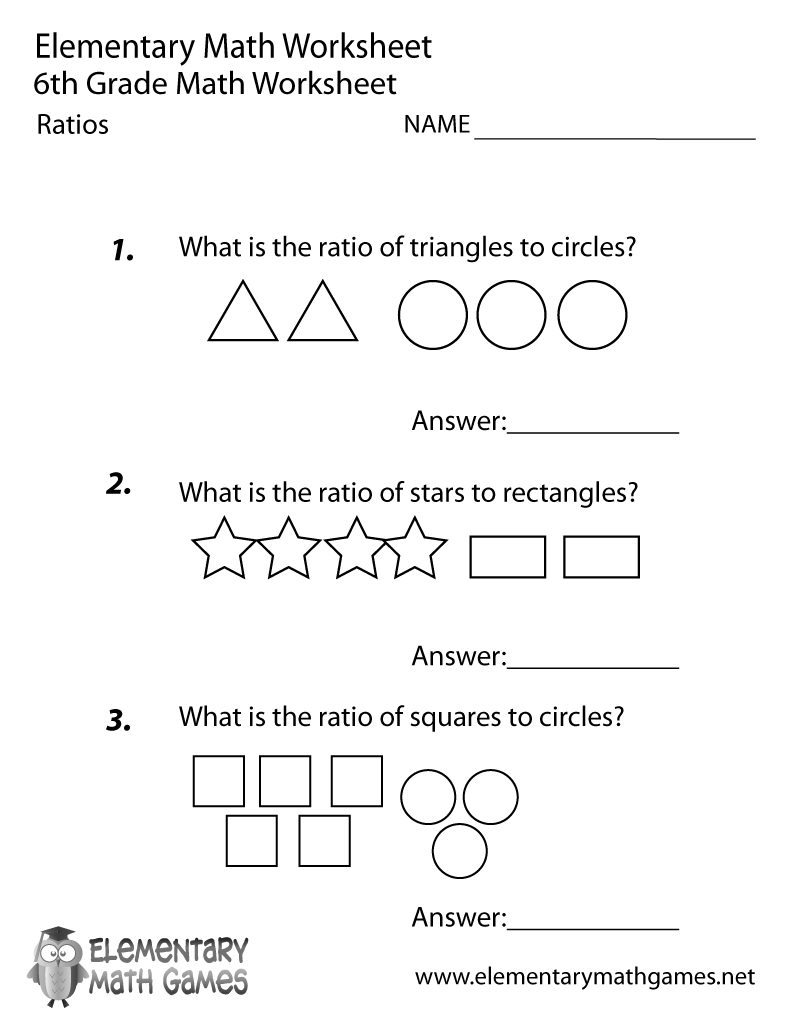
  6 Grade Math Ratios and Proportion Worksheets

---

  6th Grade Ratio Worksheets

---

  6th Grade Math Ratio Worksheets

---

  Ratio and Proportion Worksheets

---

  Equivalent Fractions Worksheet 5th Grade

---

  6th Grade Math Worksheets Algebra

---

  7th Grade Equivalent Ratios Worksheet

---

  Proportion Word Problems

---

What is a ratio?

A ratio is a mathematical comparison between two quantities, expressing how many times one quantity is contained within another. It is typically written in the form of a:b or a/b, where a and b are numbers. Ratios are used to simplify and compare relationships between different quantities or values.

How is a ratio written?

A ratio is written as a comparison of two numbers or quantities separated by a colon (":") or a forward slash ("/"). For example, a ratio of apples to oranges could be written as "3:2" or "3/2", indicating that there are 3 apples for every 2 oranges.

What is the difference between a ratio and a fraction?

A ratio is a comparison of two quantities represented by a division or colon, while a fraction is a numerical representation of a part of a whole, with a numerator representing the part and a denominator representing the whole. Ratios compare two quantities in relation to each other, while fractions represent a part-to-whole relationship.

How can ratios be simplified?

Ratios can be simplified by dividing both parts of the ratio by their greatest common factor. This process reduces the ratio to its simplest form while maintaining the same relationship between the two quantities. By simplifying ratios, it becomes easier to compare quantities and perform mathematical operations involving ratios.

How can ratios be expressed in different forms?

Ratios can be expressed in different forms by being written as fractions, using a colon between the numbers, or as a written statement. They can also be simplified or converted to equivalent ratios by multiplying or dividing both parts of the ratio by the same number. Additionally, ratios can be represented as percentages or decimals for easier comparison and analysis.

How are equivalent ratios determined?

Equivalent ratios are determined by multiplying or dividing both parts of a ratio by the same non-zero number. For example, if you have a ratio of 2:3, you can find an equivalent ratio by multiplying both parts by 2 to get 4:6 or dividing both parts by 3 to get 2/3, maintaining the same ratio relationship while showing different proportions.

What is the concept of a proportion?

A proportion is a statement that two ratios are equal. It means that two fractions or two ratios are equivalent to each other, showing the relationship between the compared values. In other words, it asserts that the part is to the whole as one part is to a quantity that includes the first whole. This mathematical concept is used to compare quantities and solve for unknown values in various real-world situations.

How can ratios be used to solve problems involving real-life situations?

Ratios can be used in real-life situations to compare quantities, set up proportions, and find unknown values. For example, if a recipe calls for 2 cups of flour for every 1 cup of sugar, you can use this ratio to adjust the ingredient amounts based on the desired batch size. Ratios can also be used in financial situations, where you can compare expenses to incomes, or in engineering, where they can be used to calculate dimensions or scale drawings. By understanding and applying ratios, you can analyze and solve a wide range of real-life problems efficiently and accurately.

What is the relationship between ratios and rates?

Ratios and rates are closely related in that both involve comparing quantities. Ratios compare the relationship between two quantities, such as 3:2, while rates compare how one quantity changes in relation to another quantity, such as 60 miles per hour. Rates can be seen as a specific type of ratio that includes units of measurement, indicating the change in quantity over a specific amount of time or another defined unit.

How can ratios be represented on a number line?

Ratios can be represented on a number line by converting the ratio to a decimal or fraction and then plotting that value on the number line. For example, if the ratio is 3:5, you can represent this as 0.6 or 3/5 on the number line. This allows for a visual representation that shows the relationship between the two quantities in the ratio.