Proportion Worksheet High School
A proportion worksheet is a valuable tool for high school students looking to reinforce their understanding of ratios and proportions. Designed to provide practice and mastery of this essential mathematical concept, a proportion worksheet presents students with a series of problems that require them to solve for missing values in proportional relationships. By working through these exercises, students can sharpen their skills and build confidence in their ability to work with ratios and proportions effectively.
Table of Images 👆
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is a proportion in mathematics?
In mathematics, a proportion is an equation that states two ratios are equal. It is a mathematical relationship between two or more quantities that shows they are in balance or have a constant ratio. Proportions are commonly used in various mathematical problems, such as in solving for unknown values or comparing quantities.
How do you solve a proportion equation?
To solve a proportion equation, cross-multiply the terms to obtain a new equation, then isolate the variable by dividing both sides by the coefficient next to it. Ensure to simplify any fractions and check your solution by plugging it back into the original equation to confirm its correctness.
How can you identify if two ratios are proportional?
Two ratios are proportional if they are equivalent, meaning their cross products are equal. To check if two ratios are proportional, you can cross multiply the terms in the numerator and denominator of each ratio. If the two cross products are equal, then the ratios are proportional. For example, if the ratios are a:b and c:d, then you would check if a*d = b*c. If they are equal, the ratios are proportional.
What is the difference between direct and inverse proportions?
Direct proportions occur when two quantities increase or decrease together, meaning that as one quantity increases, the other also increases at a consistent rate. In contrast, inverse proportions happen when one quantity increases as the other decreases, and vice versa, while the overall product of the two quantities remains constant. So, in direct proportions, the variables move in the same direction, while in inverse proportions, they move in opposite directions.
How can you use proportions to solve real-world problems, such as scaling up a recipe?
Proportions can be used to scale up a recipe by comparing the original ingredients to the desired quantity. By setting up a proportion with the original recipe as one ratio and the new quantity as the other ratio, you can solve for the amount of each ingredient needed. For example, if a recipe calls for 2 cups of flour to make 12 cookies and you want to make 24 cookies, you can set up the proportion 2/12 = x/24 and solve for x to determine that you need 4 cups of flour. This method ensures that the ingredients are scaled accurately to maintain the same taste and consistency in the final product.
What are some common misconceptions or errors students make when solving proportions?
One common misconception students have when solving proportions is that they can cross multiply any set of numbers in a proportion. However, it is important to understand that cross multiplying should only be done when setting up proportions with two fractions equal to each other. Students also often forget to simplify fractions before cross multiplying, leading to incorrect solutions. Additionally, some students mistakenly flip the numbers in the proportion when solving, resulting in the wrong answer. It is essential for students to carefully follow the correct steps and rules when solving proportions to avoid these common errors.
How can cross-multiplication be used to solve proportions?
Cross-multiplication can be used to solve proportions by multiplying the numerator of one ratio by the denominator of the other ratio, and vice versa, then setting the two products equal to each other. This allows you to find the missing value in the proportion and solve for the unknown variable.
How can you determine if a set of data exhibits a proportional relationship?
To determine if a set of data exhibits a proportional relationship, you can plot the data points on a graph and see if they fall on a straight line that passes through the origin (0,0). If the data points form a straight line that passes through the origin, then the data exhibits a proportional relationship. Additionally, you can calculate the ratio of any two data points to see if it remains constant throughout the data set. If the ratio is the same for all pairs of data points, then the data exhibits a proportional relationship.
What are some strategies for finding the missing value in a proportion?
To find the missing value in a proportion, you can set up an equation by cross-multiplying the given values to create two equivalent fractions, then solve for the unknown value by dividing or multiplying as necessary. Another approach is to use the scale factor by comparing the known values in the proportion to find the missing value. Additionally, you can use the concept of ratios and proportions to find the missing value by setting up a proportion with the known values and the unknown value, then solve for the missing value by cross-multiplying.
How can you graph proportional relationships on a coordinate plane?
To graph proportional relationships on a coordinate plane, you can plot points that represent different pairs of values from the relationship. Since proportional relationships follow the form y = kx, where k is the constant of proportionality, as you plot points, you can see that they fall on a straight line that passes through the origin (0,0) with a slope equal to the constant of proportionality. By connecting the points, you can create the line that represents the proportional relationship on the coordinate plane.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.








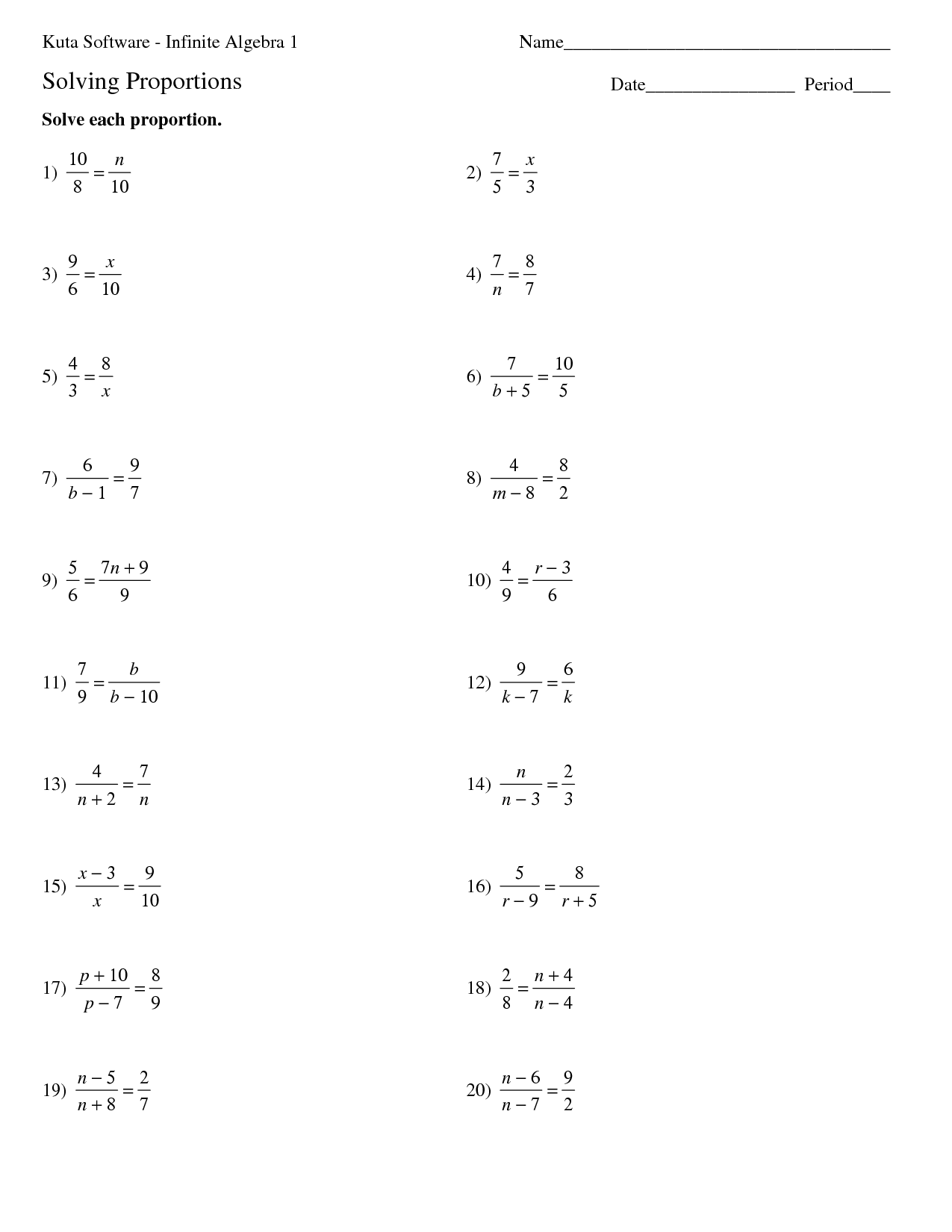














Comments