Properties of Exponents Worksheet and Answers
Are you a student or educator in need of a comprehensive worksheet to reinforce the concepts of properties of exponents? Look no further! In this blog post, we will explore a well-designed properties of exponents worksheet along with detailed answers. This resource is perfect for middle school and high school students who are striving to deepen their understanding of exponents and their applications.
Table of Images 👆
- Algebra 2 Factoring Polynomials Worksheet with Answers
- Adding Fractions with Variables
- Glencoe Algebra 2 Answer Key Chapter 4
- Properties of Exponents Worksheet Answer Key
- Exponential and Logarithmic Equations Worksheet
- Translating Algebraic Expressions Worksheets
- Equivalent Expressions Worksheets
- 6th Grade Long Division Worksheets
- Simplifying Expressions Worksheets 7th Grade
- Addition Word Problem Worksheet
- Addition Word Problem Worksheet
- Addition Word Problem Worksheet
- Addition Word Problem Worksheet
- Addition Word Problem Worksheet
- Addition Word Problem Worksheet
- Addition Word Problem Worksheet
- Addition Word Problem Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is the rule for multiplying exponents with the same base?
When you are multiplying exponents with the same base, you can simply add the exponents together. For example, when you multiply x raised to the power of a with x raised to the power of b, the result is x raised to the power of (a+b). This rule holds true for any base when multiplying exponents.
How do you divide exponents with the same base?
When dividing exponents with the same base, you subtract the exponent in the denominator from the exponent in the numerator. So for example, if you have x^3 ÷ x^2, you would subtract 2 from 3 to get x^(3-2) = x^1, which simplifies to x.
Explain the power of a power rule in exponents.
The power of a power rule in exponents states that when a term with an exponent is raised to another power, you can simply multiply the exponents. For example, (a^m)^n = a^(m*n). This rule allows for simplifying and manipulating expressions involving exponents by combining and multiplying them efficiently. It helps in performing calculations and simplifications in algebraic expressions and can make complex problems more manageable and easier to solve.
How does the zero exponent property work?
The zero exponent property states that any base raised to the power of zero equals one. This means that for any nonzero number a, a^0 = 1. This property is a fundamental rule in exponentiation and follows the convention that any number raised to the power of zero will always result in one, irrespective of the base.
Describe the product of powers rule in exponents.
The product of powers rule states that when you multiply two numbers with the same base but different exponents, you can simplify by adding the exponents together while keeping the base the same. For example, if you have x^a * x^b, this is equal to x^(a+b). This rule makes it easier to simplify and manipulate expressions involving exponents with the same base.
What is the quotient of powers rule and how does it work?
The quotient of powers rule states that when dividing two powers with the same base, you can subtract the exponents. For example, in the expression \(a^m \div a^n\), where \(m\) and \(n\) are integers, we can simplify it as \(a^{m-n}\). This rule works because when you divide two powers with the same base, you are essentially canceling out the common base and subtracting the exponents to find the new power.
Explain the power of a product rule in exponents.
The product rule in exponents states that when multiplying two exponential terms with the same base, you can add their exponents together. This is a powerful rule because it simplifies complex expressions involving exponential terms and allows for easier calculations. It helps in combining like terms, reducing the number of steps needed to solve problems, and making it easier to manipulate and compare exponential expressions. Ultimately, the product rule in exponents saves time and effort in algebraic calculations.
How does the negative exponent property function in exponents?
In exponents, the negative exponent property states that a number raised to a negative exponent can be rewritten as the reciprocal of the same number raised to the positive exponent. For example, x^-n is equal to 1/x^n. This property allows us to simplify expressions and perform calculations involving negative exponents more easily.
Describe the power of a quotient rule and its application in exponents.
The quotient rule in algebra allows us to simplify expressions by dividing two functions and finding their derivative. In exponents, the quotient rule can be used to simplify expressions involving division of exponential terms. By subtracting the exponent in the denominator from the exponent in the numerator, we can rewrite the expression as a single exponential term. This makes it easier to manipulate and solve complex exponential equations, providing a powerful tool for simplifying calculations involving exponents.
What is the rule for a negative exponent in the denominator?
When a negative exponent appears in the denominator of a fraction, you can move it to the numerator by changing its sign from negative to positive. This means that x^-n in the denominator becomes 1/x^n in the numerator.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





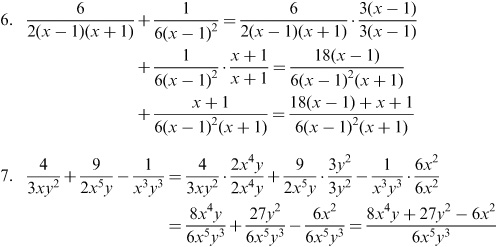




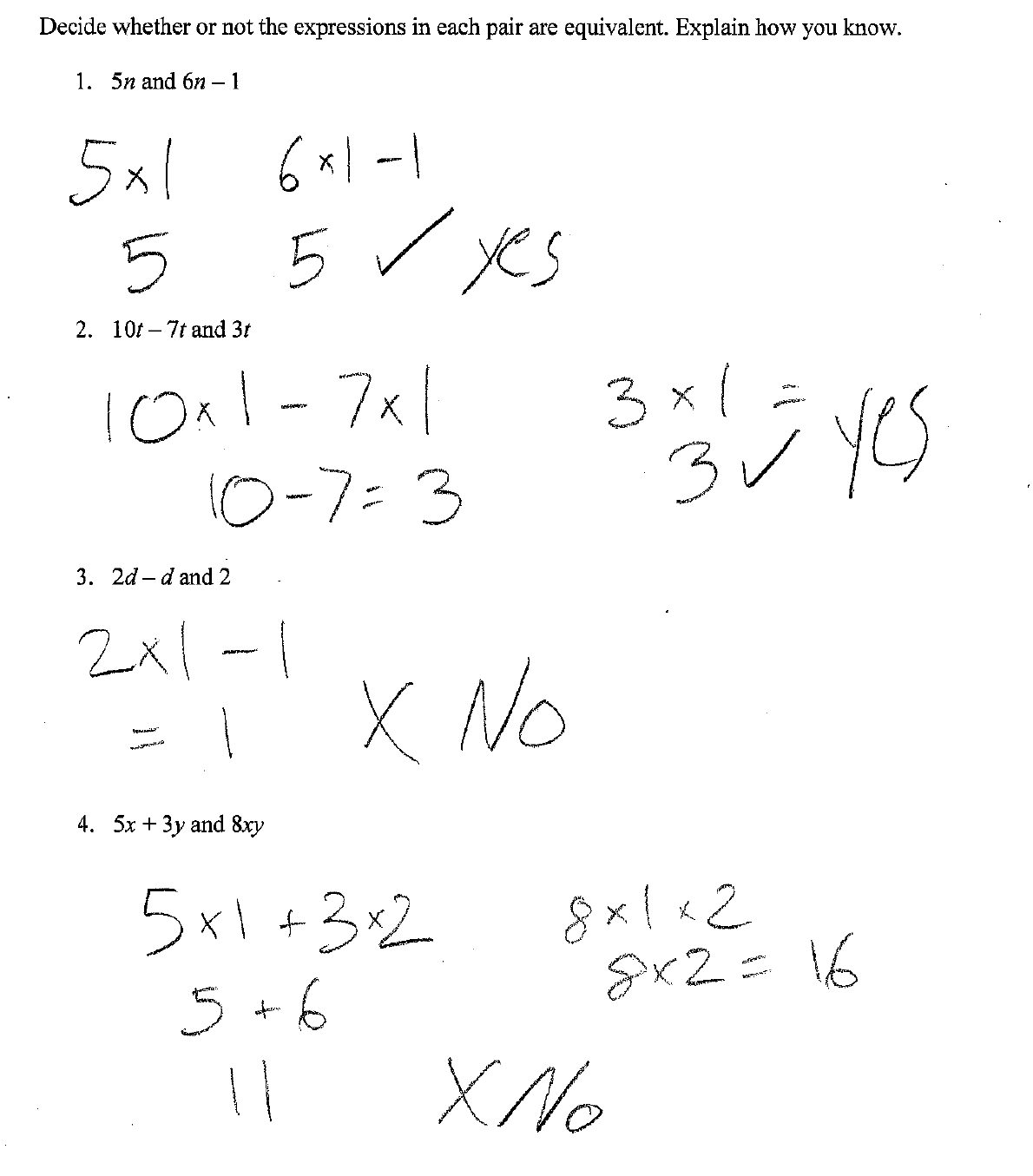
























Comments