Pre-Calc Practice Problems Worksheets
Pre-calculus practice problems worksheets provide essential practice and reinforcement for students seeking to master the concepts and skills required for success in pre-calculus courses. These worksheets offer a variety of problems covering topics such as algebraic expressions, functions, trigonometry, and more, enabling students to hone their understanding and solidify their knowledge. Whether you are a high school student preparing for a college-level pre-calculus course or an educator looking for supplemental materials, these worksheets are a valuable resource for mastering pre-calculus.
Table of Images 👆
- 12th Grade Pre Calculus Problems
- Trigonometric Functions Worksheet
- Exponential Equations Worksheets with Answers
- Pre Calculus Math Problems Worksheets
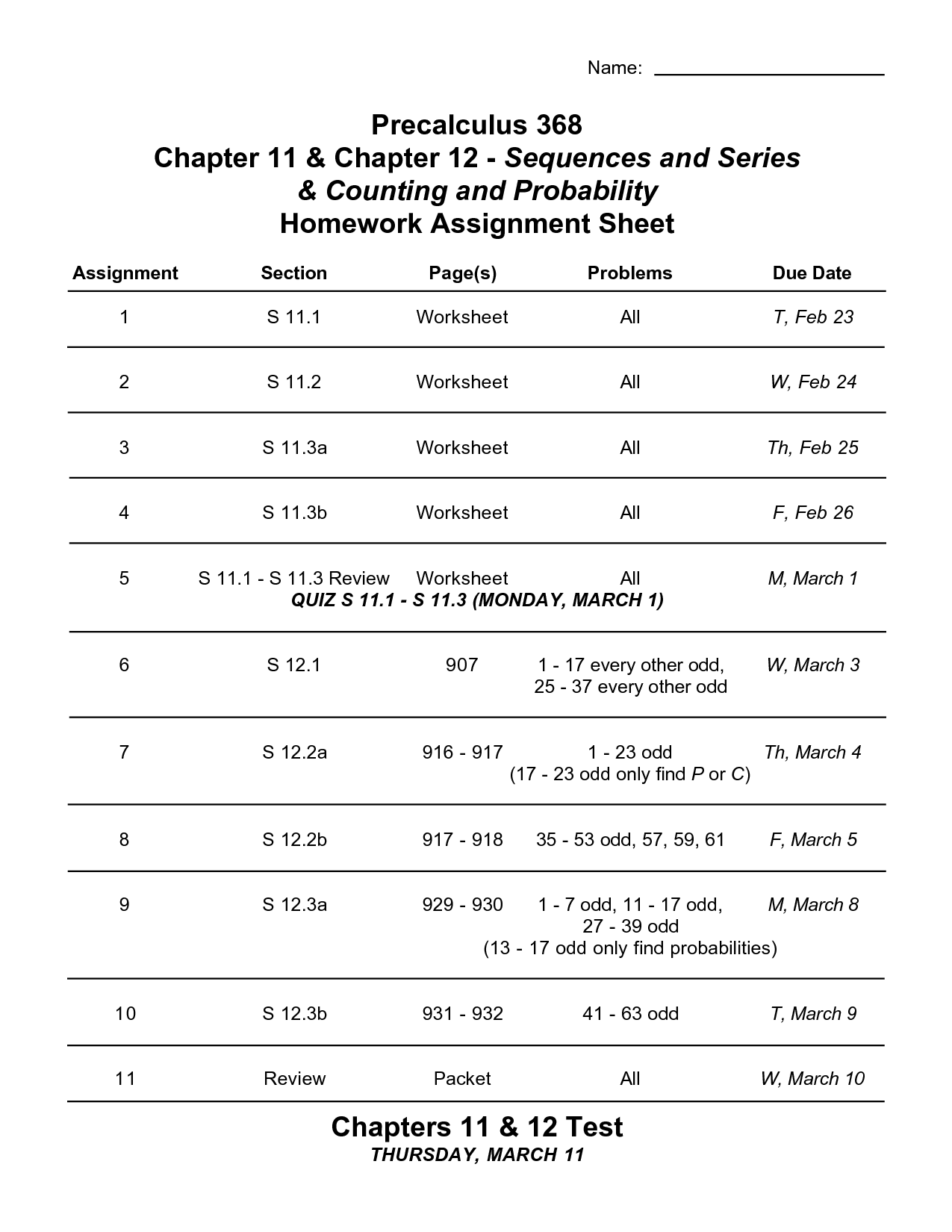
- Calculus Series and Sequences Cheat Sheet
- Precalculus Algebra Problems and Answers
- Matrix Practice Worksheet
- Calculus Math Problems Worksheet
- AP Calculus AB Free Response Answers
- Domain and Range Interval Notation Worksheet
- Pre Calculus Limits Worksheet
- Factoring Quadratic Expressions Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the difference between a quadratic equation and a linear equation?
The main difference between a quadratic equation and a linear equation is the highest power of the variable involved. In a linear equation, the highest power of the variable is 1, and the equation represents a straight line on a graph. In contrast, a quadratic equation has the highest power of 2, which results in a curved shape when graphed. So, while linear equations have a constant rate of change, quadratic equations have a varying rate of change.
How do you determine the domain and range of a function?
To determine the domain of a function, you identify all possible input values that the function can accept without causing undefined results. This involves looking for restrictions such as dividing by zero, taking the square root of a negative number, or having a negative number inside an even root. The range of a function, on the other hand, is the set of all possible output values that the function can produce. You can find the range by evaluating the function for all possible input values in its domain and identifying the corresponding output values.
What is the midpoint formula and how is it used?
The midpoint formula is used to find the point that lies exactly halfway between two given points on a line segment. It is calculated by averaging the x-coordinates and y-coordinates of the two points separately. The formula is ( (x1 + x2) / 2, (y1 + y2) / 2 ), where (x1, y1) and (x2, y2) are the coordinates of the two points. This midpoint can be used in geometry to determine the center of a line segment or to find the middle point between two locations on a map, for example.
How do you find the vertex of a parabola?
To find the vertex of a parabola in the form of y = ax^2 + bx + c, you can use the formula x = -b/2a to find the x-coordinate of the vertex. Once you have the x-coordinate, you can substitute it back into the original equation to find the corresponding y-coordinate. The vertex of the parabola is the point (x, y) where the parabola reaches its minimum or maximum value.
What is the unit circle and why is it important in trigonometry?
The unit circle is a circle with a radius of 1 centered at the origin on the Cartesian plane. In trigonometry, it is important because it serves as a fundamental tool in understanding the relationships between the trigonometric functions (sine, cosine, and tangent) and angles. The unit circle allows for easy visualization of these relationships and simplifies calculations involving trigonometric functions. It also helps in solving trigonometric equations and understanding properties of periodic functions.
How do you solve a system of equations using substitution?
To solve a system of equations using substitution, solve one equation for one variable and then substitute that expression into the other equation. This allows you to solve for the other variable. Finally, substitute the value of the second variable back into one of the original equations to find the value of the first variable. This method helps to find the values of both variables in the system of equations.
What is the difference between an arithmetic sequence and a geometric sequence?
An arithmetic sequence is a sequence of numbers where each term is obtained by adding a constant difference to the previous term, while a geometric sequence is a sequence of numbers where each term is obtained by multiplying the previous term by a constant ratio. In other words, in an arithmetic sequence, the difference between consecutive terms is constant, whereas in a geometric sequence, the ratio between consecutive terms is constant.
How do you factor a polynomial expression using the GCF method?
To factor a polynomial expression using the greatest common factor (GCF) method, first identify the greatest common factor of all the coefficients and variables in the expression. Then, divide each term of the polynomial by the GCF and rewrite the polynomial as a product of the GCF and the resulting quotient. This process helps to simplify the polynomial expression by factoring out the common factor.
What are the properties of logarithms and how are they used in solving equations?
Logarithms have properties such as the product rule, quotient rule, and power rule, which allow for simplifying complex expressions. When solving equations, logarithms are used to isolate variables that are in the exponent, transforming them into simpler equations that can be easily solved. By using properties of logarithms, equations involving exponential functions can be rewritten in a way that makes it easier to find the solutions.
How do you graph a rational function and identify its asymptotes?
To graph a rational function, first factor the numerator and denominator to simplify the function. Identify any x-intercepts by setting the numerator equal to zero and solving for x. Next, identify any vertical asymptotes by setting the denominator equal to zero and solving for x. Horizontal asymptotes can be found by comparing the degree of the numerator and denominator. If the degrees are the same, divide the leading coefficients to find the horizontal asymptote. If the degree of the numerator is smaller, the x-axis is the horizontal asymptote. Plot these points and asymptotes on the graph to sketch the rational function accurately.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.










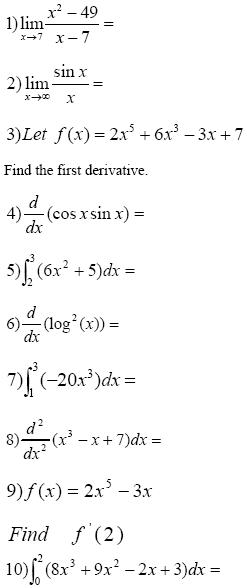

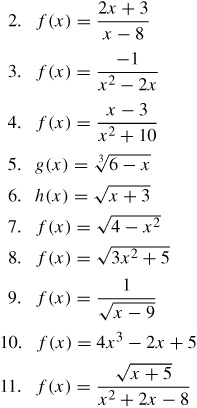
















Comments