Pre- Algebra Worksheets Distributive Property
Are you searching for effective learning tools to help your pre-algebra students understand the concept of distributive property? Look no further! Our collection of pre-algebra worksheets on distributive property is designed to provide targeted practice and reinforce essential skills. These worksheets are perfect for teachers looking to engage their students in dynamic learning activities and for parents seeking additional resources to support their child's mathematical development.
Table of Images 👆
- Distributive Property Math Algebra Worksheets
- Algebra Distributive Property Examples
- Distributive Property and Combining Like Terms Worksheet
- Equations with Distributive Property Worksheet
- Distributive Property Worksheets
- Distributive Property Worksheet Algebra 1
- GED Math Practice Worksheets Printable
- Two-Step Equations Worksheet
- Pre-Algebra Distributive Property
- Distributive Property Notes
- Pre-Algebra Worksheets Distributive Property
- Pre-Algebra Distributive Property
- Distributive Property Worksheets with Answers
- Simplifying Expressions Worksheets 7th Grade
- Distributive Property Worksheets
- Algebra Math Worksheets Printable
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What does the distributive property state?
The distributive property states that when you multiply a sum by a number, you can multiply each term in the sum by that number and then add the results. In mathematical terms, it can be written as: a * (b + c) = a * b + a * c, where a, b, and c are numbers.
How does the distributive property work with multiplication?
The distributive property states that when multiplying a number by a sum, you can also multiply that number by each addend separately and then add the products together. For example, when you have a(b + c), you can distribute the a to both b and c, giving you ab + ac. This property simplifies multiplication by breaking down complex expressions into simpler ones.
How does the distributive property work with addition?
The distributive property states that when you multiply a number by a sum, you can distribute the multiplication to each term within the sum individually. In the context of addition, the distributive property of addition states that you can distribute a number to each term within a parenthesis that is being added together. For example, 2 x (3 + 4) is the same as 2 x 3 + 2 x 4, resulting in 14.
Can the distributive property be used with subtraction?
Yes, the distributive property can be used with subtraction. It states that for any real numbers a, b, and c, a(b - c) = ab - ac. This means that you can distribute a number outside of parentheses to both terms inside, whether it involves addition or subtraction.
How can the distributive property be used to simplify expressions?
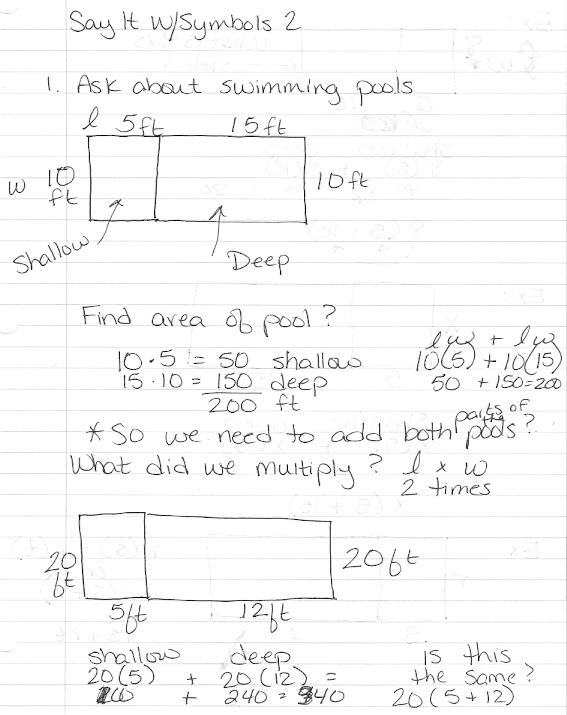
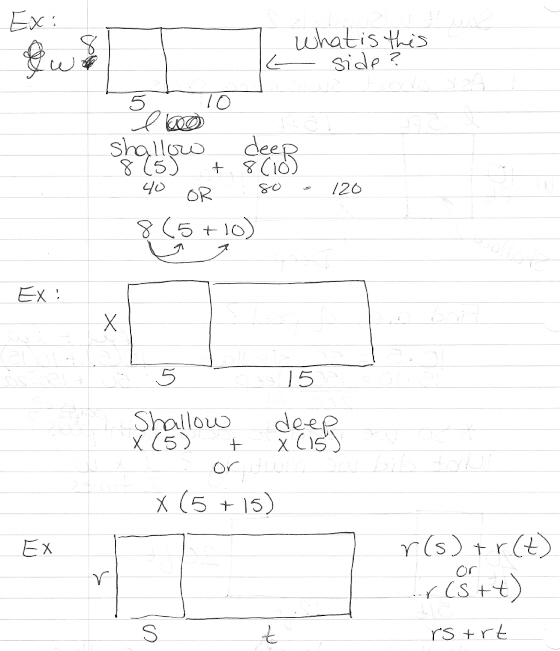
The distributive property allows you to distribute or multiply a term outside a parenthesis with each term inside the parenthesis. This can help simplify expressions by combining like terms and reducing the overall complexity of the expression. By applying the distributive property, you can reorganize terms and make the expression easier to evaluate or manipulate, leading to a more concise and streamlined form.
How can you apply the distributive property to solve equations?
To apply the distributive property to solve equations, you can distribute a number or variable to each term inside the parentheses. This allows you to simplify the equation by multiplying the value outside the parentheses with every term inside. By distributing and combining like terms, you can isolate the variable and solve for its value. Remember to perform the same operation on both sides of the equation to keep it balanced.
Can the distributive property be used with variables?
Yes, the distributive property can be used with variables. It states that for any real numbers a, b, and c, the property holds true: a(b + c) = ab + ac. This property can be applied to algebraic expressions involving variables by distributing the coefficient to each term inside the parentheses.
Can the distributive property be used with fractions or decimals?
Yes, the distributive property can be used with fractions or decimals. For fractions, you can distribute a common factor to the numerator or denominator of each fraction in the expression. Similarly, for decimals, you can distribute a common factor to each decimal place in the expression. The distributive property holds true for all types of numbers, including fractions and decimals.
Can the distributive property be used with exponents or powers?
Yes, the distributive property can be used with exponents or powers. When applying the distributive property to expressions with exponents, you can distribute the exponent to each term inside the parentheses. This means that you can multiply the terms inside the parentheses by the exponent outside the parentheses.
How can the distributive property be used to expand expressions?
The distributive property allows us to multiply a number outside of parentheses by each term inside the parentheses. By applying this property, we can distribute the multiplication and expand expressions. For example, when given an expression like 3(x + 2), we can distribute the 3 to both x and 2 by multiplying 3*x and 3*2, resulting in 3x + 6. This method can be used to simplify and break down more complex expressions by distributing the multiplication to each term within the parentheses.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





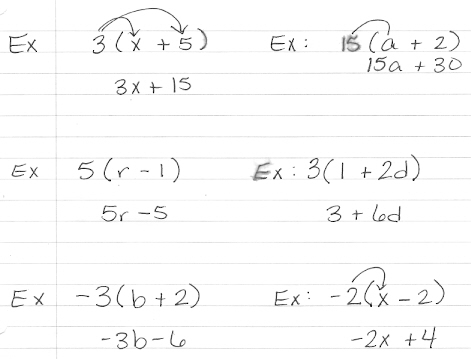



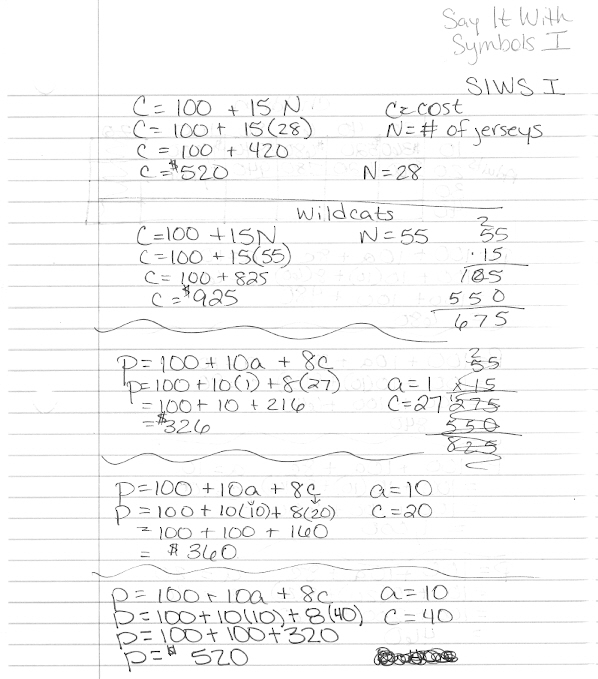




















Comments