Pre-Algebra Functions Worksheet

Are you a pre-algebra student looking for a comprehensive worksheet to practice functions? Look no further! This Pre-Algebra Functions Worksheet is designed to help you sharpen your understanding of functions and their properties. With a focus on entity and subject, this worksheet is tailored to fit the needs of pre-algebra students looking to improve their skills in functions.

  Function Tables Worksheets

---

  Linear Equations Slope-Intercept Worksheets

---

  Coordinate Plane Worksheets 6th Grade

---

  8th Grade Pre-Algebra Math Worksheets

---

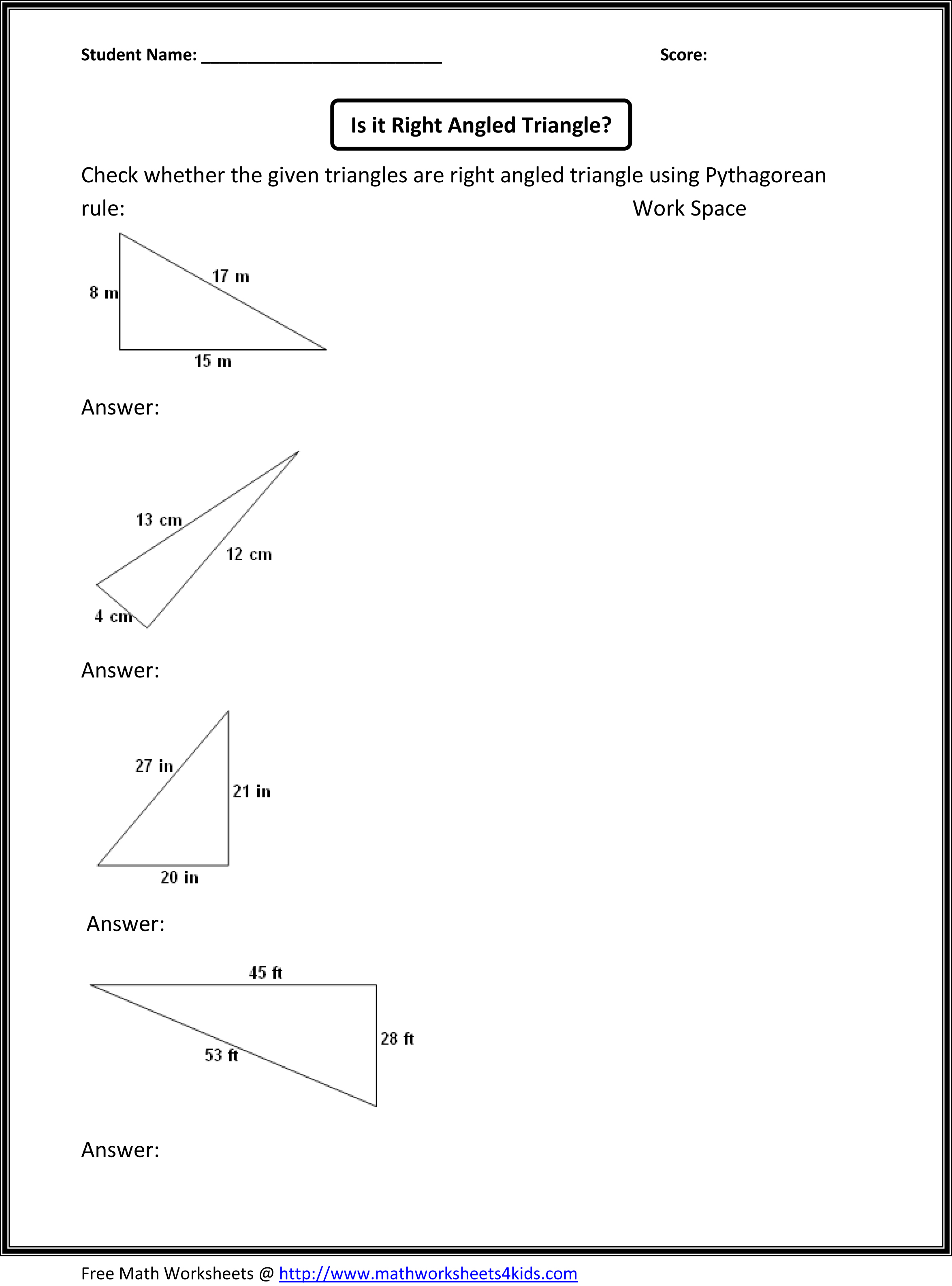
  8th Grade Math Worksheets Geometry

---

  Evaluating Algebraic Expressions Worksheets

---

  Homework Pre-Algebra Worksheets

---

  7th Grade Math Worksheets

---

  Algebra Math Color by Number

---

  Exponential Functions and Geometric Sequences Worksheet

---

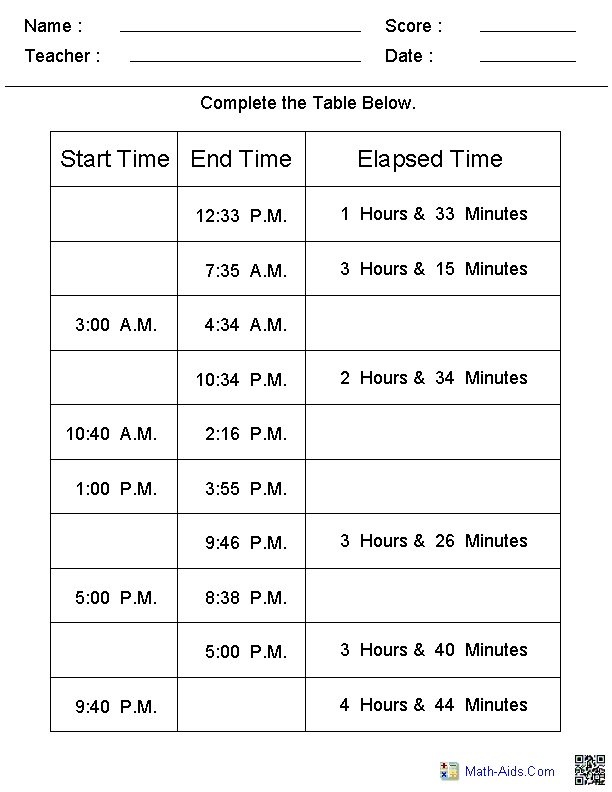
  Table Elapsed Time Worksheets

---

  Probability Graphic Organizer

---

  Kuta Software Infinite Algebra 1 Answers Key

---

  Define Ordinal Number

---

What is a function?

A function is a relation between a set of inputs and a set of possible outputs where each input is related to exactly one output. In simpler terms, a function is like a machine that takes an input (or multiple inputs) and produces a unique output based on defined rules or operations.

What is the domain of a function?

The domain of a function is the set of all possible input values (usually x-values) for which the function is defined. In other words, it is the set of values for which the function can produce an output. The domain determines the range of possible inputs that the function can accept, and it helps us understand the behavior and limitations of the function.

What is the range of a function?

The range of a function is the set of all possible output values that the function can produce. It is the collection of all values that the function can output when the input values are taken from the domain of the function. In simpler terms, it is the set of all y-values that result from plugging in all possible x-values into the function.

What is the difference between a linear function and a quadratic function?

A linear function represents a straight line when graphed, where the output changes at a constant rate with respect to the input, while a quadratic function represents a parabolic curve when graphed, where the output changes at an increasing or decreasing rate with respect to the input. In terms of their equations, a linear function is of the form y = mx + b, where m is the slope and b is the y-intercept, while a quadratic function is of the form y = ax^2 + bx + c, where a, b, and c are coefficients affecting the concavity and position of the curve.

How do you determine if a relation is a function or not?

To determine if a relation is a function or not, you need to check if each input value (x) corresponds to exactly one output value (y). If there is any x-value that maps to more than one y-value, the relation is not a function. Another way to determine if a relation is a function is to use the vertical line test - if a vertical line intersects the graph of the relation at more than one point, then the relation is not a function.

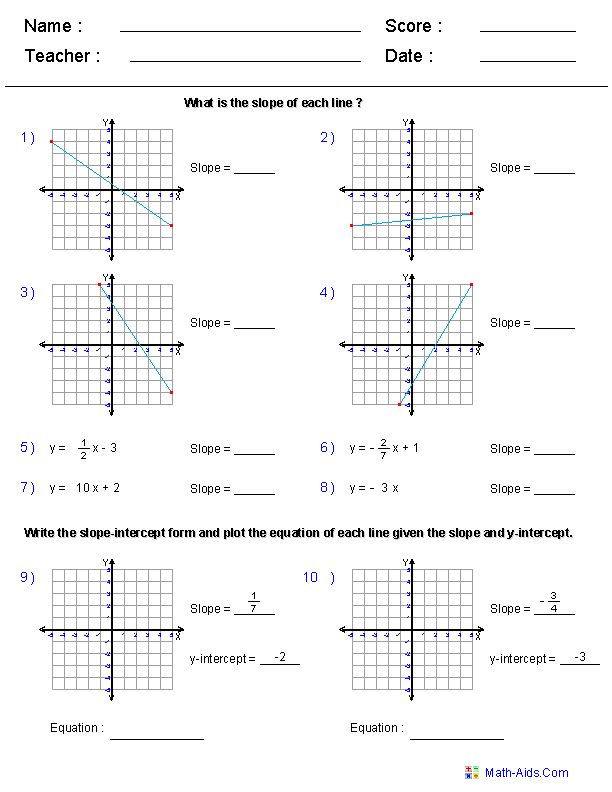
How do you find the slope of a linear function?

To find the slope of a linear function, you would calculate the change in the y-coordinates divided by the change in the x-coordinates between any two points on the line. This is often represented as (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line. The resulting value is the slope of the linear function.

What is the equation of a line in slope-intercept form?

The equation of a line in slope-intercept form is y = mx + b, where m is the slope of the line and b is the y-intercept, the point where the line intersects the y-axis. This form allows for easy visualization of the slope and intercept of the line on a graph.

How do you solve a system of linear equations?

To solve a system of linear equations, you typically use methods such as substitution, elimination, or matrices. The goal is to find the values of the variables that satisfy all the equations in the system simultaneously. By manipulating the equations and solving for one variable at a time, you can determine the solution to the system. If the system has a unique solution, it will be a specific point in the coordinate plane where all the equations intersect.

What is the nth term of an arithmetic sequence?

The nth term of an arithmetic sequence is given by the formula \( a_n = a_1 + (n-1)d \), where \( a_n \) is the nth term, \( a_1 \) is the first term, \( n \) is the term number, and \( d \) is the common difference between consecutive terms.

How do you graph a quadratic function?

To graph a quadratic function, first identify the values of the coefficients a, b, and c in the general form of a quadratic equation y = ax^2 + bx + c. Locate the vertex of the parabola which is given by the formula x = -b/2a. Plot the vertex on the coordinate plane. Next, find two additional points on either side of the vertex by using different x values and calculating the corresponding y values using the equation. Plot these points and draw a smooth curve through all three points to form the parabolic shape of the quadratic function.