Polynomial Functions Worksheet and Answer

Are you in search of a comprehensive and practical way to reinforce your understanding of polynomial functions? Look no further than the Polynomial Functions Worksheet and Answer key. Designed for high school students and mathematics enthusiasts, this worksheet is tailored to provide targeted practice on various topics related to polynomial functions. Whether you're a self-study learner or a teacher looking for additional resources, this worksheet will help solidify your grasp on this important mathematical concept.

  Graphing Rational Functions Worksheet Answers

---

  Factoring by Grouping Worksheet

---

  Algebra 2 Factoring Polynomials Worksheet with Answers

---

  Crossword Puzzle Fraction Worksheets

---

  Exponents

---

  Graphing Exponential Functions Worksheet Answers

---

  Who AM I Worksheet Answers

---

  Rational Root Theorem Worksheet

---

  Kuta Software Infinite Algebra 2 Factoring

---

  Graphing Quadratic Functions Worksheet Answers

---

  Algebra 1 Worksheets

---

  High School Algebra Course 2

---

  Algebra 2 Factoring Polynomials Worksheet with Answers

---

  Factoring Polynomials Worksheet Puzzle

---

  Adding Polynomials Worksheet Printable

---

  Factoring Polynomials Worksheet Puzzle

---

  Adding and Subtracting Polynomials Worksheet Answers

---

What is a polynomial function?

A polynomial function is a mathematical function that can be expressed as a sum of terms, where each term is a constant multiplied by a variable raised to a non-negative integer power. The general form of a polynomial function is f(x) = an*x^n + an-1*x^(n-1) + ... + a1*x + a0, where n is a non-negative integer, a0, a1, ..., an are constants, and x is the variable.

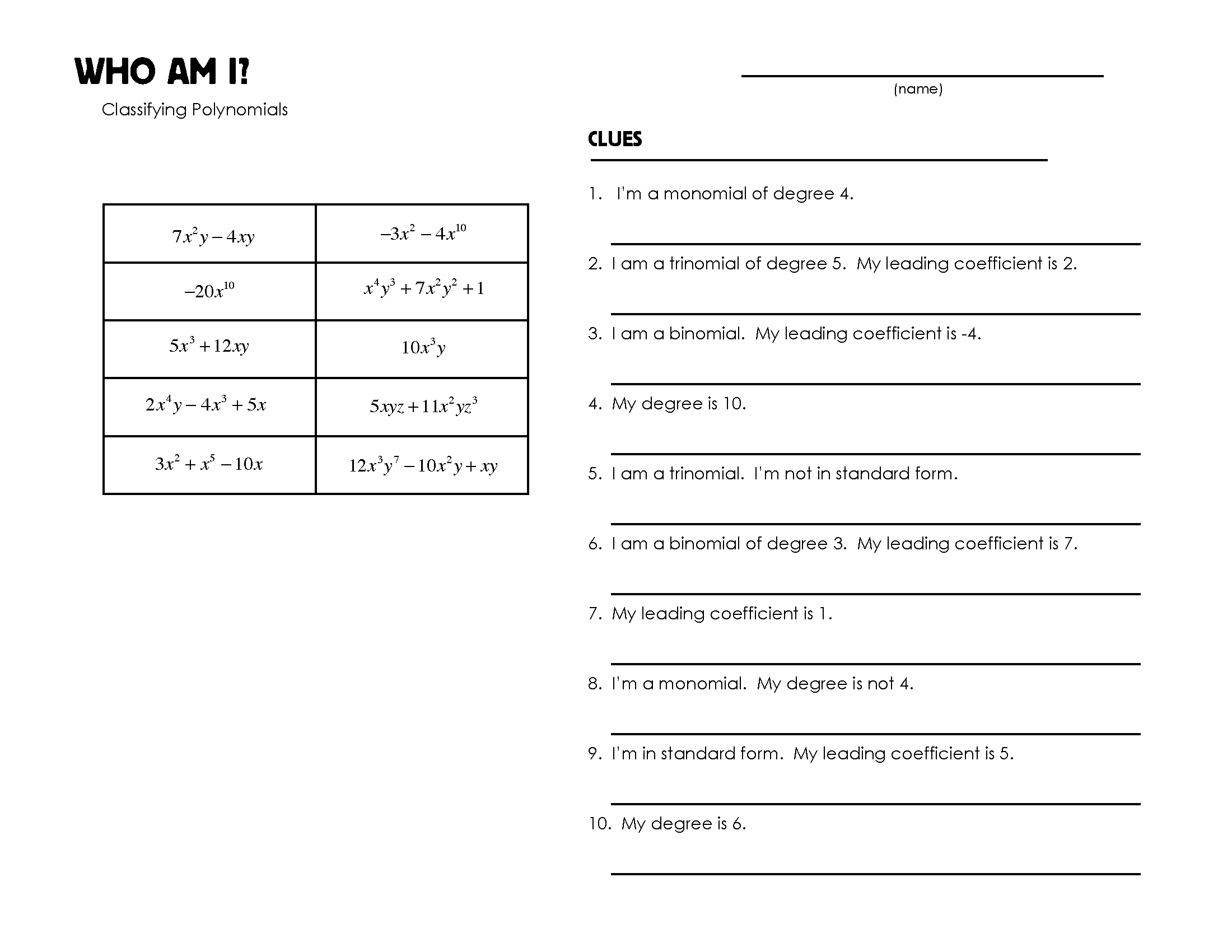
What is the degree of a polynomial function?

The degree of a polynomial function is the highest power of the variable in the polynomial expression. It is determined by looking at the exponent of the term with the highest power of the variable. The degree of a polynomial helps classify the function and provides information about its behavior.

How do you identify the leading coefficient of a polynomial function?

To identify the leading coefficient of a polynomial function, look at the term with the highest degree (the term with the highest exponent). The leading coefficient is the numerical coefficient of this term. It is the number in front of the variable with the highest exponent and is the coefficient that influences the shape and behavior of the polynomial function as the input values become large in either positive or negative direction.

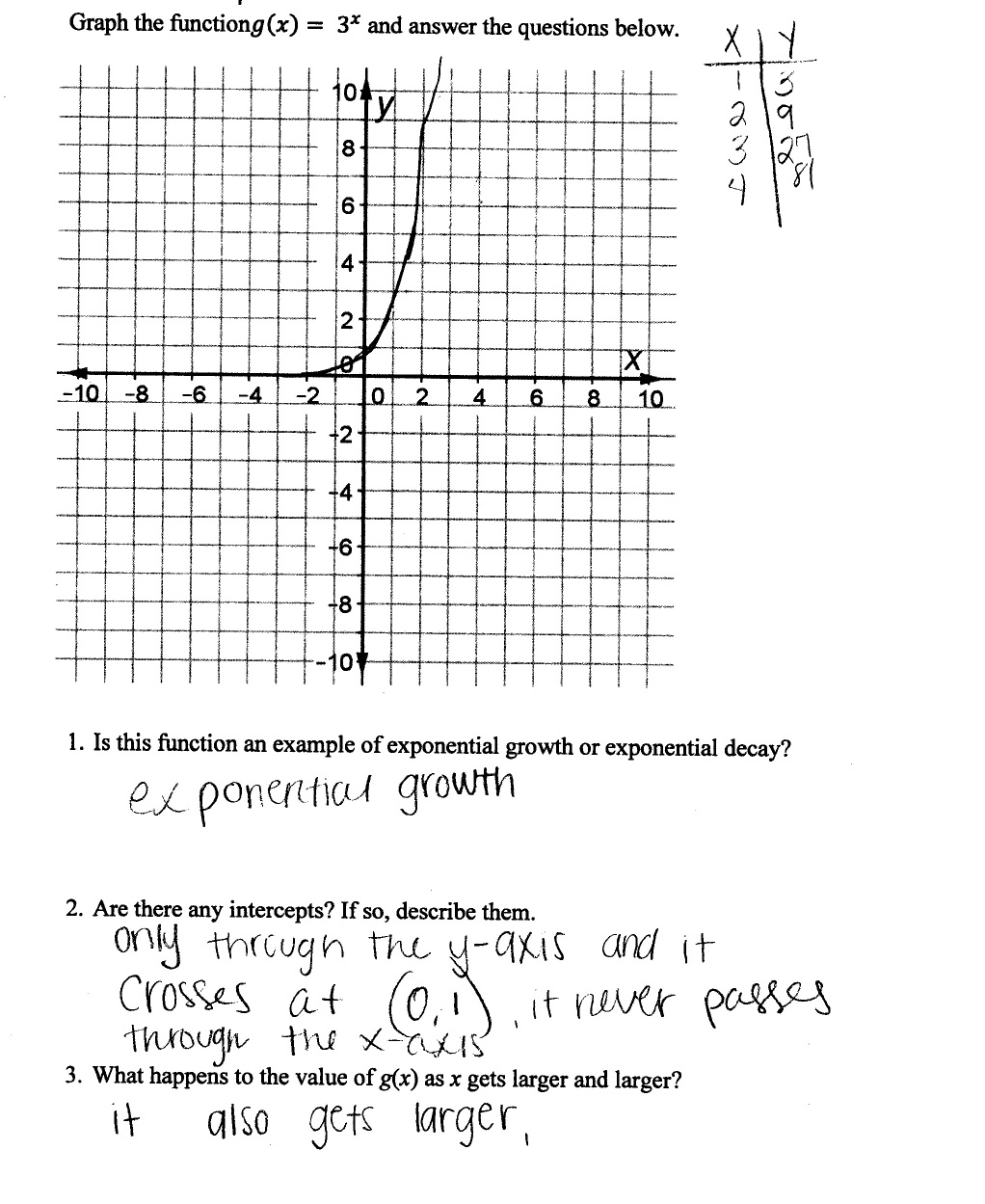
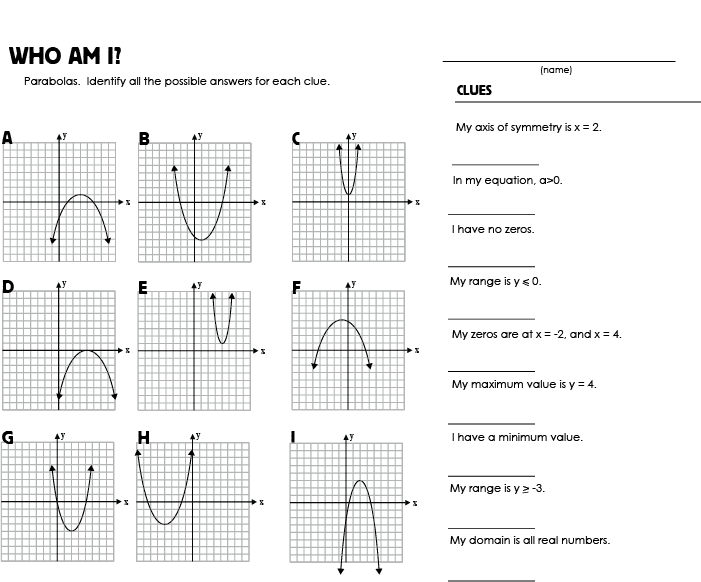
What is the end behavior of a polynomial function?

The end behavior of a polynomial function describes the behavior of the graph of the function as x approaches positive or negative infinity. It is determined by the degree and leading coefficient of the polynomial. For even-degree polynomials, the end behavior is that the graph either rises or falls to the right and left, mirroring each other. For odd-degree polynomials, the end behavior is that the graph rises to the right and falls to the left or falls to the right and rises to the left. The leading coefficient determines whether the graph ends in the positive or negative y-direction as x approaches infinity.

How do you find the x-intercepts of a polynomial function?

To find the x-intercepts of a polynomial function, set the function equal to zero and solve for the variable x. The x-intercepts are the points where the graph of the function crosses the x-axis, so finding the x-values where the function equals zero will give you the x-intercepts. It's essentially finding the roots or zeros of the function.

How do you find the y-intercept of a polynomial function?

To find the y-intercept of a polynomial function, set all the variables other than the independent variable to zero and then solve for the dependent variable. In simpler terms, plug in x=0 into the polynomial function and solve for y. The resulting value is the y-intercept of the polynomial function.

How do you determine the number of turning points a polynomial function has?

To determine the number of turning points a polynomial function has, you need to look at the degree of the polynomial. The maximum number of turning points a polynomial function can have is equal to its degree minus 1. This means that a cubic polynomial (degree 3) can have a maximum of 2 turning points. A turning point occurs when the derivative of the function changes sign, indicating a change in the direction of the function's graph.

How can you determine the relative maximum and minimum values of a polynomial function?

To determine the relative maximum and minimum values of a polynomial function, you first need to find the derivative of the function and then set it equal to zero to find the critical points. These critical points can be either relative maximum, minimum, or points of inflection. By analyzing the sign of the derivative around these critical points, you can determine whether they correspond to a relative maximum or minimum. Additionally, you can use the second derivative test to confirm the nature of these points by analyzing the concavity of the function at those critical points.

How do you use the Remainder Theorem to find factors of a polynomial function?

To use the Remainder Theorem to find factors of a polynomial function, you first evaluate the polynomial at a given value - let's call it 'c'. If the remainder of this division is 0, then (x - c) is a factor of the polynomial function. This is because if (x - c) is a factor, then when the polynomial is divided by (x - c), the remainder should be 0 according to the Remainder Theorem. If the remainder is not 0, then (x - c) is not a factor of the polynomial. This process of testing different values for 'c' allows you to find all the factors of the polynomial function.

How do you use synthetic division to divide a polynomial by a linear factor?

To use synthetic division to divide a polynomial by a linear factor, you first line up the coefficients of the terms in the polynomial in descending order. Then, you write down the root of the linear factor you are dividing by, and perform synthetic division by bringing down the first coefficient, multiplying it by the root, adding the result to the next coefficient, and repeating this process until you reach the end. The final row of numbers obtained represents the coefficients of the quotient polynomial.