Polynomial Equations Worksheet

If you're a high school or college student struggling with mastering polynomial equations, look no further than our comprehensive Polynomial Equations Worksheet. Designed specifically to help students grasp the concepts of polynomial equations, this worksheet is an invaluable resource for anyone seeking to improve their understanding and problem-solving skills in this subject.

  Solving Polynomials Worksheet

---

  Adding and Subtracting Polynomials Worksheet Answers

---

  Polynomial Functions Worksheet

---

  8th Grade Math Practice Worksheets

---

  Translating Algebraic Expressions Worksheets

---

  Graphing Rational Functions Worksheet Answers

---

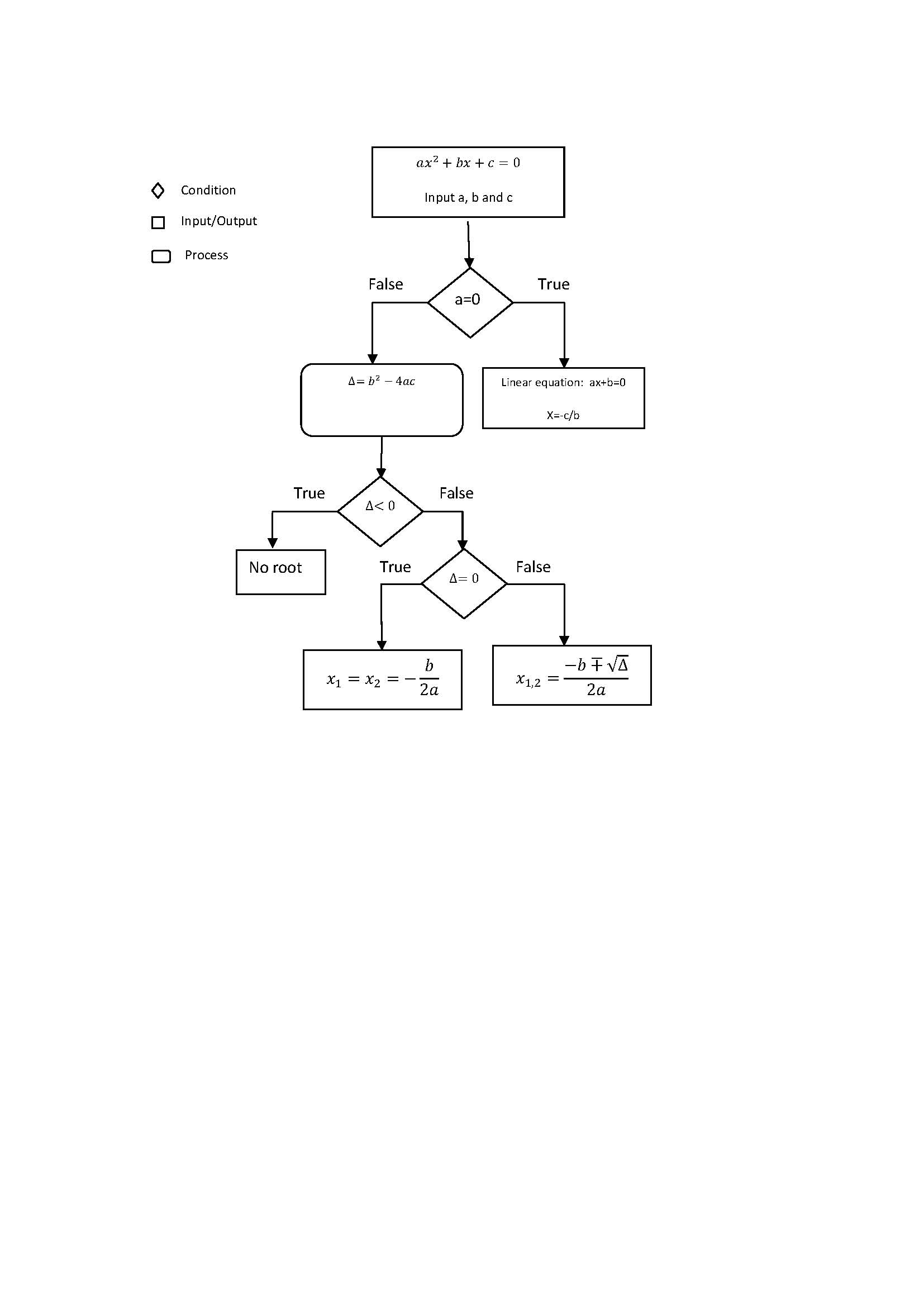
  Solving Quadratic Equations Algorithm

---

  Polynomials and Factoring Practice Worksheet Answers

---

  Solving Quadratic Equations in Factored Form

---

  How to Write a Polynomial Function in Standard Form

---

  Area Perimeter Worksheets 3rd Grade

---

  Multiplying Binomials Worksheet

---

What is a polynomial equation?

A polynomial equation is an equation where a variable is raised to non-negative integer powers, and the coefficients are constants. The equation can be written as a sum of terms, with each term being a product of a coefficient, the variable raised to a power, and possibly other variables raised to non-negative integer powers.

How do you determine the degree of a polynomial equation?

The degree of a polynomial equation is determined by the highest power of the variable in the equation. For example, in the equation 3x^2 - 5x + 1, the highest power of x is 2, so the degree of the polynomial is 2. It is important to remember that the degree of a polynomial is always a non-negative integer.

What are the coefficients of a polynomial equation?

The coefficients of a polynomial equation are the numbers that multiply each term with a variable raised to a certain power. For example, in the polynomial equation 3x^2 + 5x - 2, the coefficients are 3, 5, and -2. These coefficients determine the shape and behavior of the polynomial when graphed or solved algebraically.

Define a linear equation and give an example.

A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable raised to the first power. It represents a straight line on a graph, where the variable is plotted on the x-axis and the constant term is the y-intercept. An example of a linear equation is y = 3x + 5.

What is a quadratic equation? Give an example.

A quadratic equation is a second-degree polynomial equation in one variable that can be written in the form ax^2 + bx + c = 0, where a, b, and c are constants and a ? 0. An example of a quadratic equation is 2x^2 - 5x + 3 = 0.

Explain the concept of roots or solutions of a polynomial equation.

The roots or solutions of a polynomial equation are the values of the variable that make the polynomial expression equal to zero. These roots represent the points where the polynomial intersects the x-axis on a graph. The number of roots or solutions of a polynomial equation is equal to the degree of the polynomial, and they can be real or complex numbers depending on the nature of the polynomial. By finding the roots of a polynomial equation, we can solve for the values of the variable that satisfy the equation and help us understand the behavior of the polynomial function.

What is meant by the term "degree of multiplicity" in a polynomial equation?

The term "degree of multiplicity" refers to the number of times a particular root or solution appears in a polynomial equation. It indicates how many times a given factor is repeated in the factored form of the polynomial. This is important in understanding the behavior of the graph of the polynomial at that particular root, as it impacts the way the graph intersects the x-axis at that point.

Differentiate between a monomial, binomial, and trinomial equation.

A monomial is an algebraic expression with only one term, such as "3x" or "5x^2." A binomial has two terms, like "4x + 2" or "6xy - 3." A trinomial, on the other hand, contains three terms, for example, "2x^2 + 5x - 3." So, the main difference lies in the number of terms each type of equation possesses - monomial has one term, binomial has two terms, and trinomial has three terms.

How do you solve a polynomial equation algebraically?

To solve a polynomial equation algebraically, you can use various methods such as factoring, the quadratic formula, synthetic division, or polynomial long division. The goal is to manipulate the equation to isolate the variable on one side of the equation and find its roots, or solutions, by setting the equation equal to zero and then solving for the variable. By applying these algebraic techniques, you can determine the values of the variable that satisfy the polynomial equation.

Provide at least two real-life examples where polynomial equations are used.

Polynomial equations are commonly used in various real-life applications such as in physics, where they are used to model the motion of objects under the influence of forces (e.g., projectile motion or harmonic motion). Another example is in finance, where polynomial equations are used to analyze and predict market trends, price fluctuations, and risk assessments.