Perfect Cubes Worksheet

Are you in search of a comprehensive worksheet to reinforce your understanding of perfect cubes? Look no further! This blog post will introduce you to a high-quality worksheet that focuses on perfect cubes, perfect for middle school students or anyone looking to master this mathematical concept.

  Perfect Square Roots Worksheet

---

  Factoring Polynomials Worksheet

---

  Factoring Perfect Cubes Formula

---

  Square Numbers Worksheet

---

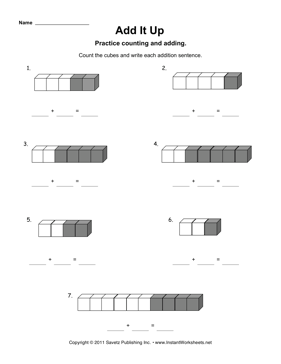
  Addition Math Cubes Worksheet

---

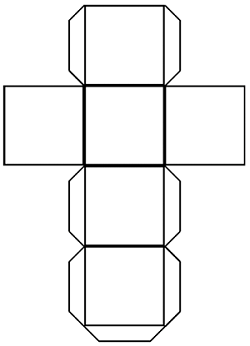
  Paper Cube Template

---

  Perfect Square Root Chart

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

  4 Digit Addition with Regrouping Worksheets

---

What is a perfect cube?

A perfect cube is a number that can be expressed as the cube of an integer. In other words, a perfect cube is the result of multiplying a number by itself three times. For example, 27 is a perfect cube because it is the result of multiplying 3 by itself three times (3 x 3 x 3 = 27).

How do you determine if a number is a perfect cube?

To determine if a number is a perfect cube, you need to find the cube root of the number and check if it is a whole number. If the cube root is an integer without any decimal or fractional part, then the number is a perfect cube. For example, the cube root of 27 is 3 (3 x 3 x 3 = 27), indicating that 27 is a perfect cube.

How many perfect cubes are there between 1 and 100?

There are four perfect cubes between 1 and 100, which are 1 (1^3), 8 (2^3), 27 (3^3), and 64 (4^3).

What is the cube root of a perfect cube?

The cube root of a perfect cube is the number that, when multiplied by itself twice, gives the perfect cube. In mathematical terms, if a number X is a perfect cube, then the cube root of X is the number Y such that Y * Y * Y = X.

Give an example of a perfect cube.

One example of a perfect cube is 27, as it is the result of multiplying 3 by itself twice (3 x 3 x 3 = 27), making it a perfect cube.

Is 64 a perfect cube? Why or why not?

Yes, 64 is a perfect cube because it is the cube of the integer 4, as 4 x 4 x 4 = 64. In other words, 64 can be expressed as 4^3, making it a perfect cube.

Can a negative number be a perfect cube? Why or why not?

Yes, a negative number can be a perfect cube. A perfect cube is a number that can be expressed as the cube of an integer, regardless of whether it is positive or negative. When a negative number is cubed, the result is also a negative number. For example, (-2) cubed equals -8. Thus, negative numbers can indeed be perfect cubes.

How do you find the cube root of a perfect cube?

To find the cube root of a perfect cube, you need to take the number and raise it to the power of 1/3. For example, if you have a perfect cube like 64, you would calculate the cube root by taking the cube root of 64, which equals 4. This is because 4 cubed equals 64.

How can you check if a number is a perfect cube using prime factorization?

To check if a number is a perfect cube using prime factorization, first find the prime factors of the given number. Then, check if each prime factor appears in groups of three. If all prime factors appear in groups of three, the number is a perfect cube. If any prime factor is not in groups of three, the number is not a perfect cube.

How can you determine if a number is a perfect cube without using a calculator?

To determine if a number is a perfect cube without using a calculator, you can try to find the prime factorization of the number and see if each prime factor appears in groups of three. If each prime factor appears in groups of three, then the number is a perfect cube. For example, if the prime factorization of a number is 2^3 * 3^2 * 5, then it is not a perfect cube because the prime factor 3 does not appear in a group of three.