Percent Equation Worksheets

Are you a math teacher or a parent looking for high-quality worksheets to help your students or children practice solving percent equations? Look no further! In this blog post, we will explore a variety of entity and subject worksheets that are designed to engage and challenge students while reinforcing their understanding of percent equations.

  6th Grade Math Worksheets Algebra

---

  Fifth Grade Math Worksheets

---

  7th Grade Math Worksheets Percent of Change

---

  These Basics for Algebra 1 Worksheets

---

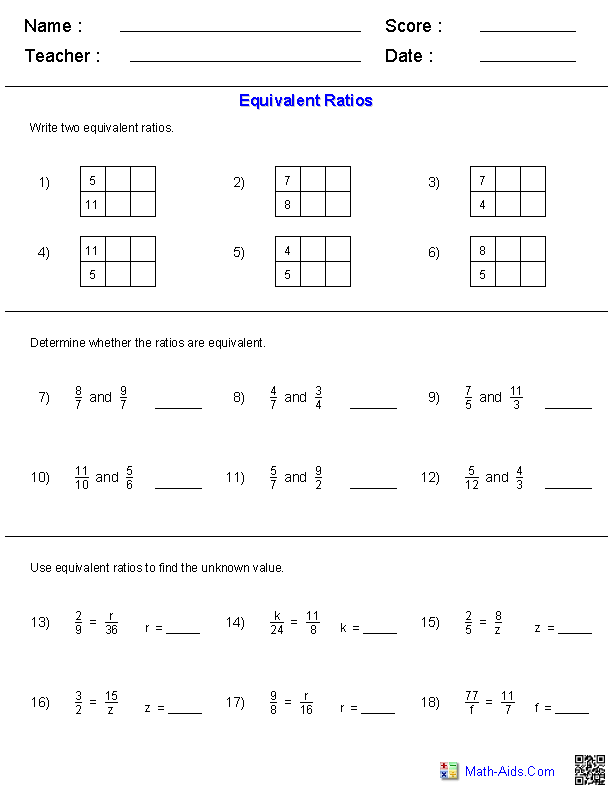
  7th Grade Equivalent Ratios Worksheet

---

  Convert Decimal to Fraction Worksheet

---

  8th Grade Math Vocabulary Worksheets

---

  Multi-Step Math Word Problems Worksheets

---

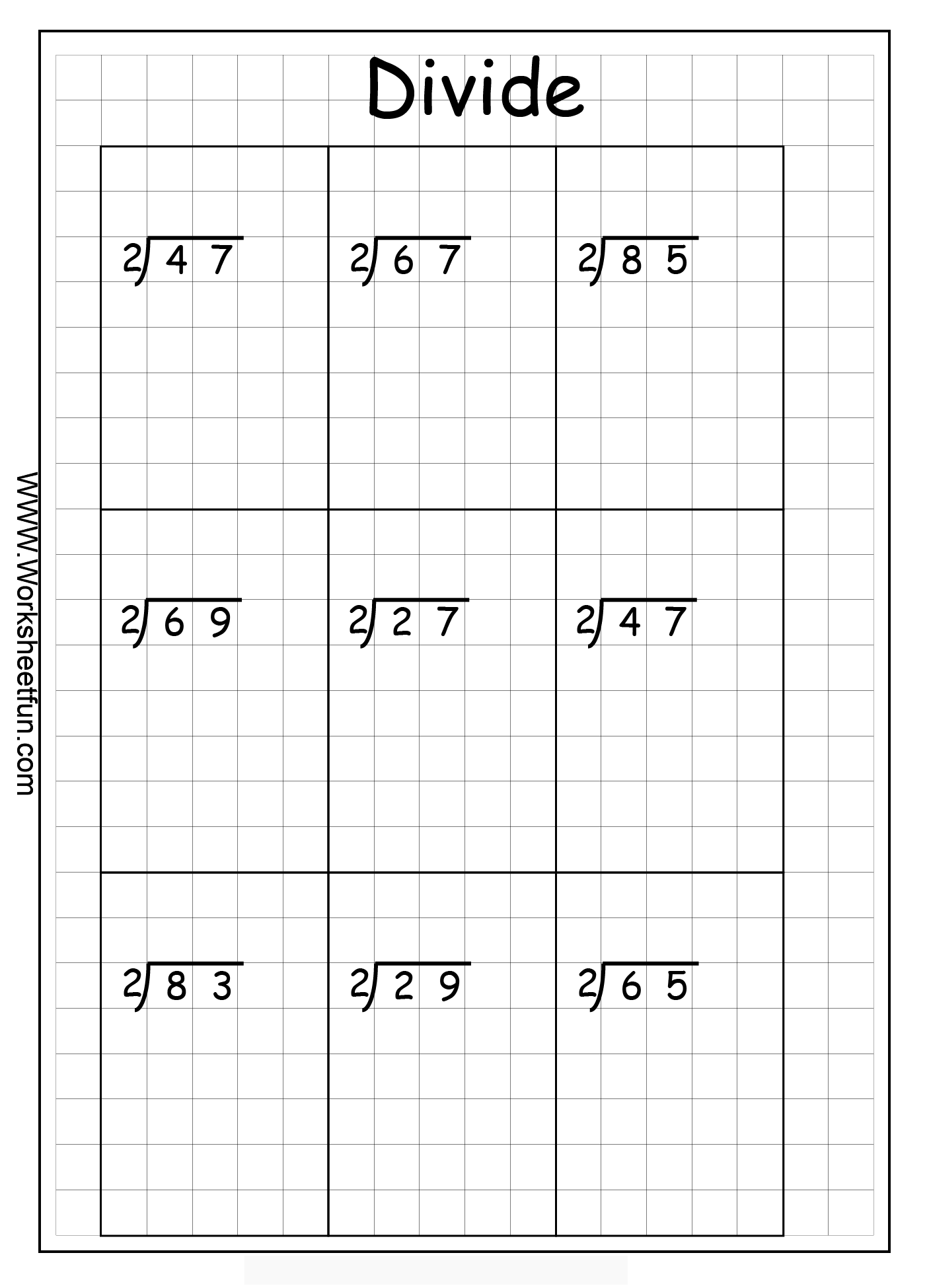
  Long Division Worksheets by 2

---

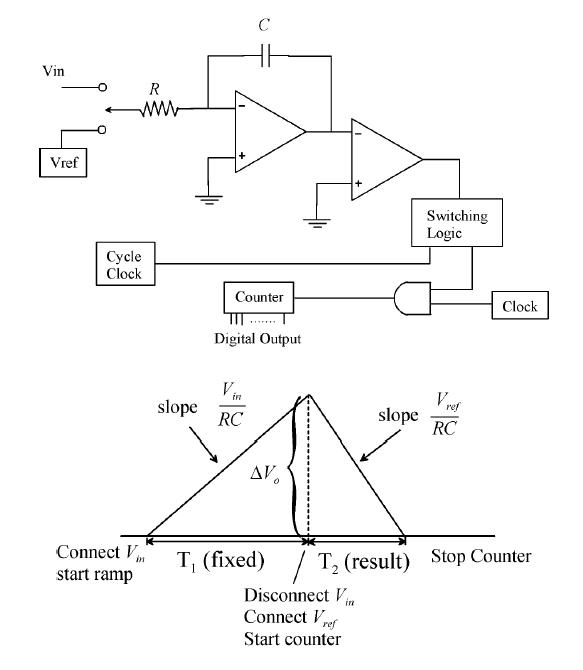
  Dual Slope ADC

---

  4th Grade Math Worksheets Fractions

---

  5th Grade PEMDAS Worksheets Order Operations

---

  Fundamental Counting Principle Worksheet

---

  Fundamental Counting Principle Worksheet

---

  Fundamental Counting Principle Worksheet

---

  Fundamental Counting Principle Worksheet

---

What is the percent equation used for?

The percent equation is used to calculate the value of a percentage of a given number. It is commonly used in various real-life situations, such as calculating discounts, taxes, tips, commissions, and interest rates. By using the percent equation, you can easily determine the amount of increase or decrease in a value based on a specified percentage.

How do you calculate the percent equation?

To calculate a percent equation, you can use the formula: part = percent x whole / 100. This formula helps you find the part or the percentage of a whole number. To calculate the percentage, multiply the percent value by the whole and divide by 100. If you are trying to find the whole or total value, you can rearrange the formula to be whole = part / (percent / 100). Just plug in the values you have and solve for the unknown variable to find the answer.

What is the formula for calculating the percent equation?

The formula for calculating the percent equation is: \( \text{Part} = \left(\frac{\text{Percent}}{100}\right) \times \text{Whole} \), where "Part" is the quantity being calculated, "Percent" is the percentage being used, and "Whole" is the total quantity or value.

Can the percent equation be used for different situations?

Yes, the percent equation can be used for various situations where a percentage of a total value needs to be calculated. Whether it's finding a percentage increase or decrease, calculating sales tax or discounts, or determining the proportion of a total, the percent equation can be applied to a wide range of real-world scenarios to solve for the unknown value.

Why is understanding the percent equation important in real-life scenarios?

Understanding the percent equation is important in real-life scenarios because it allows individuals to calculate discounts, taxes, tips, interest rates, and many other financial transactions. Being able to manipulate percentages helps in making informed decisions about purchases, investments, savings, and budgeting. It also enables individuals to compare different options and determine the best course of action based on their financial goals. Overall, proficiency in using the percent equation is crucial for managing personal finances effectively and making sound financial decisions.

Are there any variations or alternate methods of using the percent equation?

Yes, there are variations and alternate methods of using the percent equation. One common variation is to find the percent increase or decrease, by calculating the difference between two values and then expressing it as a percentage of the original value. Another method is to solve problems involving multiple percentages by applying the concepts of successive percentage changes. These variations and methods provide flexibility in using the percent equation in various real-world situations.

What are some common examples of percent equation problems?

Common examples of percent equation problems include calculating discounts, markups, sales tax, tips, commission, interest rates, and population growth rates. These problems involve finding values such as the original price, final price, percentage change, or the percentage itself using the formula: part = percent x whole.

Can the percent equation be used to solve complex mathematical problems?

Yes, the percent equation can be used to solve complex mathematical problems involving calculations related to percentages, such as finding percentages of quantities, determining the original amount given a percentage increase or decrease, and other related scenarios. By applying the percent equation correctly, complex mathematical problems involving percentages can be effectively solved by providing a structured and systematic approach to the calculations needed.

How can the percent equation be applied in financial calculations?

The percent equation can be applied in financial calculations to determine percentages of values, such as calculating interest rates, discounts, taxes, or profit margins. For example, to calculate the interest on a loan, you would multiply the principal amount by the annual interest rate expressed as a percentage. Similarly, to find the amount of a discount on a product, you would multiply the original price by the discount percentage. These applications of the percent equation are integral in financial decision-making and analysis.

Are there any tips or tricks for effectively using the percent equation in worksheets?

When using the percent equation in worksheets, it's important to first understand the formula: \( \text{part} = \text{percent} \times \text{whole} \). One helpful tip is to convert the percentage to a decimal before multiplying. Encourage students to clearly label the different parts of the equation (part, percent, whole) to avoid confusion. Additionally, have them practice identifying the missing value in different scenarios to strengthen their problem-solving skills. Regular practice and application of the percent equation in various contexts will help students become more proficient in using it effectively.