Multiplying and Dividing Exponents Worksheets
Do you need practice multiplying and dividing exponents? Look no further! We have created a series of worksheets specifically designed to help you master this topic. Whether you are a student studying algebra or a teacher looking for supplemental materials, our worksheets provide a variety of exercises to reinforce your understanding of multiplying and dividing exponents.
Table of Images 👆
- Multiplying and Dividing Fractions Worksheets
- Algebra 1 Worksheets
- Multiplying and Dividing Negative Exponents
- Multiplying Decimals Worksheets 5th Grade
- 5th Grade Decimal Division Worksheets
- Adding and Subtracting Integers Problems
- 6th Grade Math Worksheets Mean Median Mode
- Place Value and Multiplication Worksheets
- Fall Math Coloring Worksheets 5th Grade
- 6th Grade Math Worksheets Multiplication
- Decimal Crossword Puzzle
- 6th Grade Math Worksheets Algebra
- Subtracting Fractions Worksheets
- Doc Distance Time Graph Worksheet
- Speed Distance Time Worksheet and Answers
- Speed Distance Time Worksheet and Answers
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
What is the power rule for multiplying exponents?
The power rule for multiplying exponents states that when you multiply two exponential expressions with the same base, you can add the exponents together. This can be illustrated as: \(a^m \times a^n = a^{m+n}\), where "a" is the base and "m" and "n" are the exponents.
How do you multiply exponents with the same base?
To multiply exponents with the same base, you need to add the exponents together. This means that if you have the same base raised to different exponents, you can simply add the exponents to find the result. For example, if you have x^2 * x^3, the result would be x^(2+3) = x^5.
How do you multiply exponents with different bases?
To multiply exponents with different bases, you can raise each base to its respective exponent and then multiply the results together. For example, to multiply 2^3 and 3^2, you would calculate 2^3 = 8 and 3^2 = 9, then multiply 8 and 9 together to get 72.
What is the rule for dividing exponents with the same base?
When dividing exponents with the same base, you subtract the exponents. For example, if you have x^a / x^b, where x is the base, the result would be x^(a-b).
How do you divide exponents with different bases?
To divide exponents with different bases, you need to rewrite the bases in terms of the same base. For example, if you have \( a^x \div b^y \), you can rewrite this as \( \frac{a^x}{b^y} = \frac{a^x}{(a^{\log_a b})^y} = a^{x-y\log_a b} \). This allows you to simplify the expression and perform the division.
Can you explain the concept of zero exponents in multiplication?
Zero exponents in multiplication refer to the property that any non-zero number raised to the power of zero equals 1. This fundamental property arises from the definition of exponentiation and is a fundamental rule in algebraic manipulations. Essentially, any non-zero number raised to the power of zero always results in 1, regardless of the value of the number. It is a crucial rule to remember and apply in mathematical calculations involving exponents.
Can exponents be negative in multiplication and division? If so, explain.
Yes, exponents can be negative in multiplication and division. When an exponent is negative, it indicates that the base value should be taken as the reciprocal of the positive exponent value. For example, in multiplication, a^-n is equivalent to 1/a^n, and in division, a^-n is equivalent to 1 / a^n. This property allows us to handle fractions and reciprocals in exponent notation efficiently.
What happens when you multiply or divide exponents with negative bases?
When you multiply or divide exponents with negative bases, the rules of exponents still apply. If the negative base is raised to an even exponent, the result will be positive. However, if the negative base is raised to an odd exponent, the result will be negative. This is true for both multiplication and division of negative bases with exponents.
How does the order of operations apply to multiplying and dividing exponents?
In the order of operations, when multiplying or dividing exponents, you should perform the exponentiation operations before multiplication and division. This means that you first evaluate the exponents and then multiply or divide the resulting values. This ensures that the correct order of operations is followed and that the mathematical expression is evaluated accurately.
Can you provide an example of a word problem involving multiplying and dividing exponents?
Sure, here's an example: If a bacteria population doubles every hour, starting with 100 bacteria, how many bacteria will there be after 3 hours? To solve this problem, we need to multiply the starting amount of bacteria by 2 for each hour (2^3) to account for the exponential growth. Therefore, after 3 hours, there will be 100 x 2^3 = 800 bacteria.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






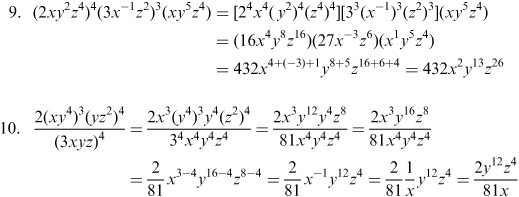

























Comments