Matrix Operations Worksheet
Are you a math enthusiast looking to practice your skills in matrix operations? Look no further! We have created a comprehensive worksheet that focuses on various matrix operations such as addition, subtraction, multiplication, and finding determinants. This worksheet is designed to provide you with ample practice to enhance your understanding of matrices and their properties. Whether you are a student preparing for an exam or simply someone wanting to sharpen your mathematical abilities, this worksheet is the perfect tool to help you achieve your goals.
Table of Images 👆
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
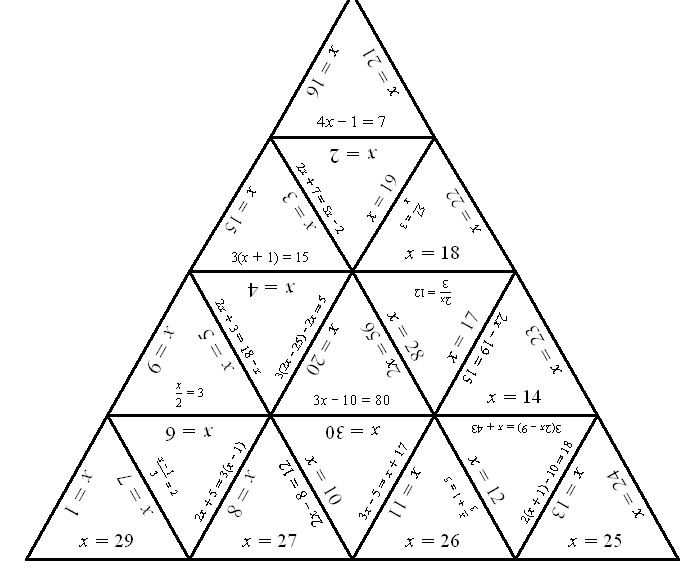
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What are matrix operations?
Matrix operations involve various mathematical operations that can be performed on matrices, such as addition, subtraction, multiplication, and division. These operations are used to manipulate and analyze data in matrix form, making calculations more efficient and allowing for complex mathematical computations to be performed effectively. Each operation has specific rules and properties that govern how matrices can be combined and manipulated to achieve desired results.
How are matrices added and subtracted?
Matrices are added and subtracted by performing element-wise addition and subtraction, respectively. This means that in order to add or subtract two matrices, you simply add or subtract the corresponding elements in each matrix. The matrices must have the same dimensions in order to be added or subtracted, otherwise the operation is not possible.
How is matrix multiplication defined?
Matrix multiplication is defined as the operation of multiplying two matrices to produce a new matrix. In order for two matrices to be multiplied, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix will have dimensions equal to the number of rows of the first matrix and the number of columns of the second matrix. Each element in the resulting matrix is obtained by taking the dot product of the corresponding row from the first matrix and the corresponding column from the second matrix.
What is the identity matrix and its properties?
The identity matrix is a square matrix where all the elements along the main diagonal are 1, and all other elements are 0. It is commonly denoted as "I" or "I_n" where n represents the size of the matrix. The main properties of the identity matrix include that it is the multiplicative identity for matrix multiplication, meaning that when multiplied by any matrix of compatible size, the identity matrix returns the original matrix. Additionally, the product of any matrix and the identity matrix is the original matrix itself. The identity matrix is also symmetric and its determinant is always 1.
How are matrices transposed?
Matrices are transposed by flipping the matrix over its main diagonal, swapping each element at position (i, j) with the element at position (j, i). This means that the rows of the original matrix become the columns of the transposed matrix, and vice versa.
What is the determinant of a matrix?
The determinant of a matrix is a scalar value that is calculated from the elements of the matrix and is used to determine properties of the matrix such as invertibility. It is a value that can be computed for a square matrix only and provides information about the scaling factor of the matrix and whether the matrix is singular or nonsingular.
How are matrices inverted?
Matrices are inverted by using the concept of the matrix inverse. The inverse of a matrix A, denoted as A^(-1), is a matrix that, when multiplied by A, results in an identity matrix. The inverse of a matrix can be calculated using various methods such as Gauss-Jordan elimination, LU decomposition, or by using software tools like MATLAB or Python libraries such as NumPy.
What are the properties of diagonal matrices?
Diagonal matrices are square matrices where all elements outside the main diagonal are zero. The main diagonal is the one that goes from the top left to the bottom right of the matrix. Diagonal matrices are easy to manipulate and compute with because many operations such as addition, subtraction, and multiplication with scalars are much simpler compared to general matrices. Additionally, the determinant of a diagonal matrix is simply the product of its diagonal elements, and the eigenvalues of a diagonal matrix are its diagonal elements.
How are matrices raised to a power?
Matrices are raised to a power using matrix multiplication. To raise a matrix A to the power n (where n is a positive integer), you simply multiply the matrix by itself n times, which means performing matrix multiplication of A with itself n-1 times. The resulting matrix will be the matrix A raised to the power n.
What is the relationship between matrix operations and linear transformations?
Matrix operations and linear transformations are closely related in that matrices can represent linear transformations. Each matrix operation (such as addition, subtraction, multiplication) corresponds to a specific type of linear transformation in terms of scaling, rotating, or shearing vectors in a vector space. The properties and behaviors of matrices directly reflect the properties and behaviors of the associated linear transformations, making matrices powerful tools for analyzing and computing with linear transformations.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






















Comments