Math Worksheets Reflection Rotation Translation

If you're searching for a comprehensive resource that helps students understand the concepts of reflection, rotation, and translation in mathematics, then you've come to the right place. Worksheets on these topics provide a structured and practical approach for learners to grasp these fundamental principles in a hands-on manner.

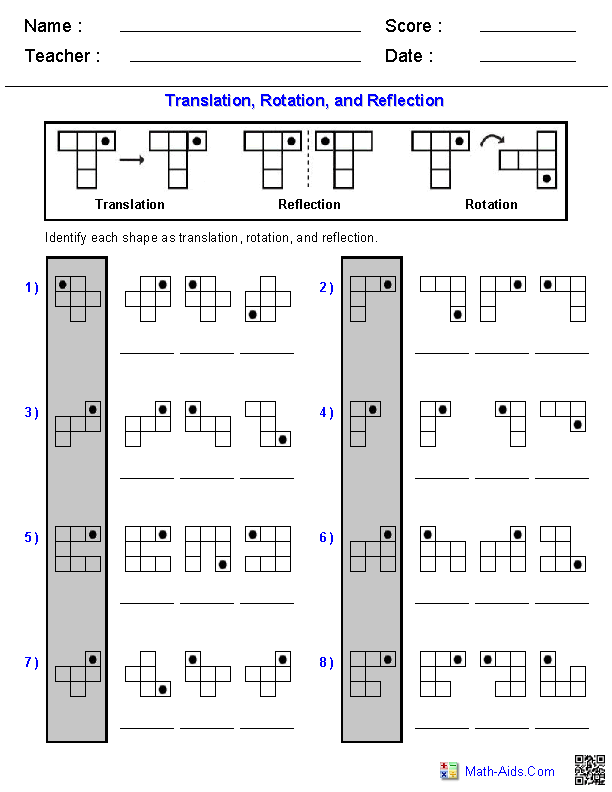
  Geometry Translation Reflection Rotation Worksheets

---

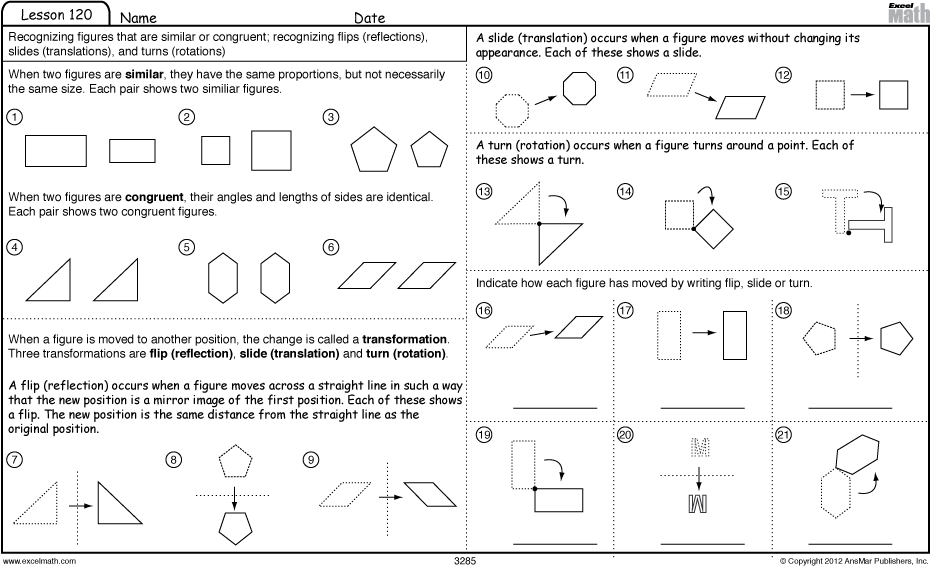
  Translation Rotation Reflection

---

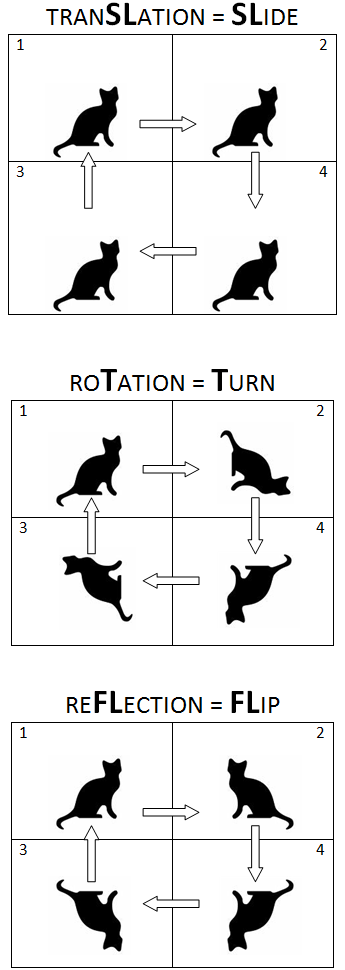
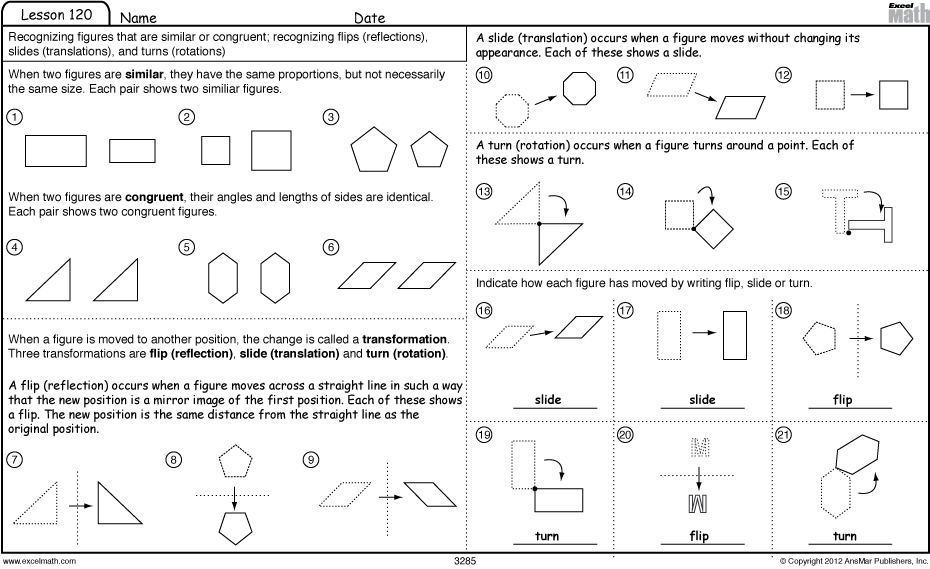
  Geometry Slide Flip Turn Worksheets

---

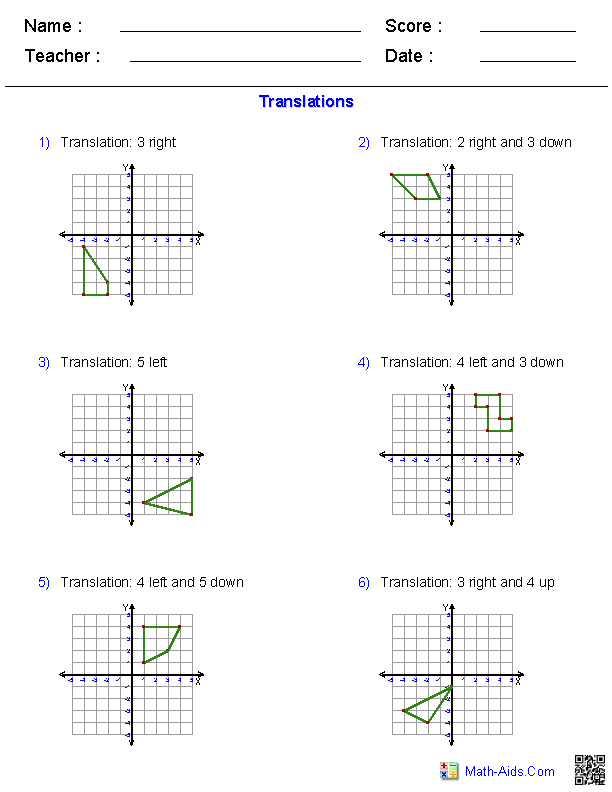
  Geometry Translations Worksheet

---

  8.G.1 Common Core Worksheet

---

  M.C. Escher Lizard Tessellation

---

  Math Worksheets Grade 3 Answers

---

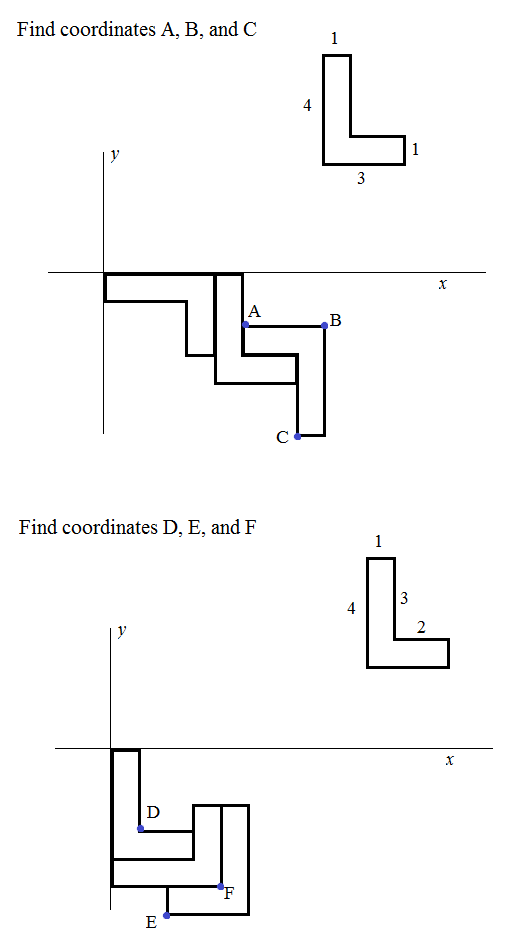
  Coordinate Plane Graphing Characters

---

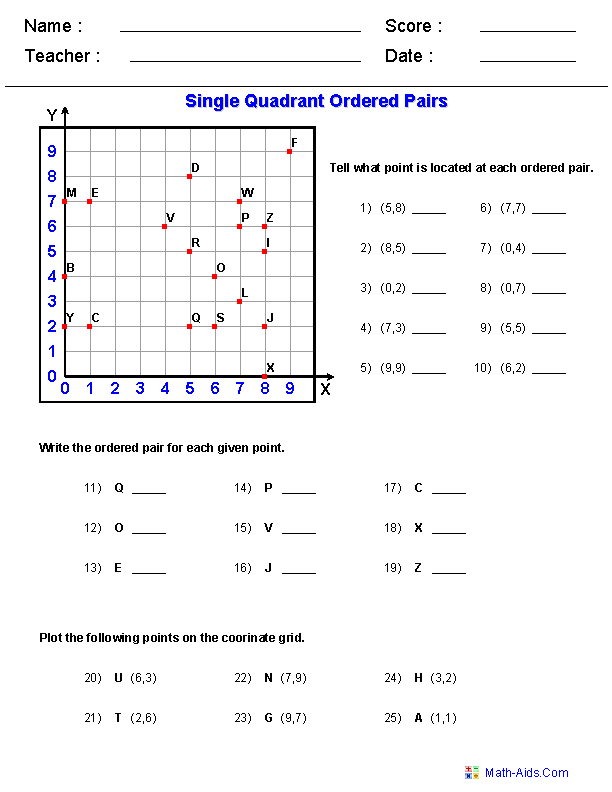
  6th Grade Graphing Ordered Pairs Worksheets

---

What is a reflection in mathematics?

A reflection in mathematics is a transformation that flips a shape over a line, creating a mirror image. It is a type of symmetry operation where every part of the shape is mirrored across the line of reflection. Reflections are commonly studied in geometry and are used to study patterns, angles, and properties of geometric figures.

How do you determine the line of reflection in a figure?

To determine the line of reflection in a figure, you need to identify points or shapes that are equidistant from the proposed line of reflection. This can be done by measuring the distance between corresponding points on the figure and ensuring that they are the same distance away from the line of reflection. The line of reflection will be the perpendicular bisector of the segment connecting the corresponding points.

What does it mean to rotate a shape in mathematics?

In mathematics, to rotate a shape means to turn it around a specific point by a certain angle. This transformation changes the orientation of the shape while keeping its size and proportions the same. Rotation is a fundamental concept in geometry and is used to describe how shapes can be transformed in space.

How do you specify the angle of rotation in a figure?

To specify the angle of rotation in a figure, you generally use degrees as the unit of measurement. You can describe the rotation by stating the number of degrees the figure has been turned either clockwise or counterclockwise from its original position. This measurement helps identify how much the figure has been rotated relative to a reference point or axis.

What is a translation in mathematics?

In mathematics, a translation is a transformation that moves every point of a shape or object the same distance in the same direction. It does not change the size, shape, or orientation of the object, only its position in space. Translations are described using vectors to denote the direction and distance of the movement.

How do you express a translation using coordinates?

To express a translation using coordinates, you would adjust the x and y coordinates of each point by the same amount in a specified direction. For example, if you want to move a point (x,y) by a translation vector (a,b), the new coordinates would be (x+a, y+b). This represents shifting the point horizontally by a units and vertically by b units.

What is the difference between a rigid transformation and a non-rigid transformation?

A rigid transformation is a transformation that preserves distances and angles between points, such as translation, rotation, and reflection, while a non-rigid transformation is a transformation that changes distances and angles between points, such as scaling and shearing. In other words, rigid transformations maintain the shape and size of an object, while non-rigid transformations distort the shape or size of the object.

How do you identify the image of a shape after a given transformation?

To identify the image of a shape after a given transformation, you need to apply the specific transformation rules to the coordinates of the shape's vertices. For example, if the transformation is a translation, you would add or subtract values from the x and y coordinates of each vertex. If the transformation is a rotation, you would use rotation rules to determine the new coordinates of the vertices. Similarly, for reflection or dilation, you would follow the corresponding rules to find the image of the shape after the transformation.

What are some real-world applications of reflections, rotations, and translations?

Reflections, rotations, and translations have a wide range of real-world applications across industries such as computer graphics, engineering, architecture, and manufacturing. For example, in computer graphics, transformations are used to create visual effects like mirroring images or rotating objects. In engineering, structural components are often designed by applying transformations to models. Architects use transformations to plan the layout of buildings and structures. Additionally, in manufacturing, transformations are used to position and manipulate objects during the production process. Overall, reflections, rotations, and translations play a crucial role in various practical applications where spatial relationships and positioning are essential.

How can you use mathematical transformations to create symmetrical patterns?

You can use mathematical transformations such as reflections, translations, rotations, and dilations to create symmetrical patterns. For example, a reflection over a line produces a mirror image of the original shape, while a rotation around a point can create rotational symmetry. By applying these transformations systematically to an initial shape, you can generate various symmetrical patterns with precision and consistency.