Math Worksheets 3rd
If you're searching for a comprehensive and efficient way to enhance your child's learning in math, look no further than Math Worksheets 3rd. These carefully crafted worksheets are designed to provide children in third grade with engaging and interactive exercises that cover a wide range of math topics. With a focus on solidifying fundamental math skills, Math Worksheets 3rd offers an effective tool for parents and educators to support their child's learning journey in mathematics.
Table of Images 👆
- Free Printable Math Worksheets 3rd Grade
- Math Worksheets
- 6th Grade Math Worksheets Mean Median Mode
- Free Thanksgiving Math Worksheets Multiplication
- Math Addition Worksheets 2nd Grade
- 4th Grade Math Worksheets
- Math Worksheets 3rd Grade Packets
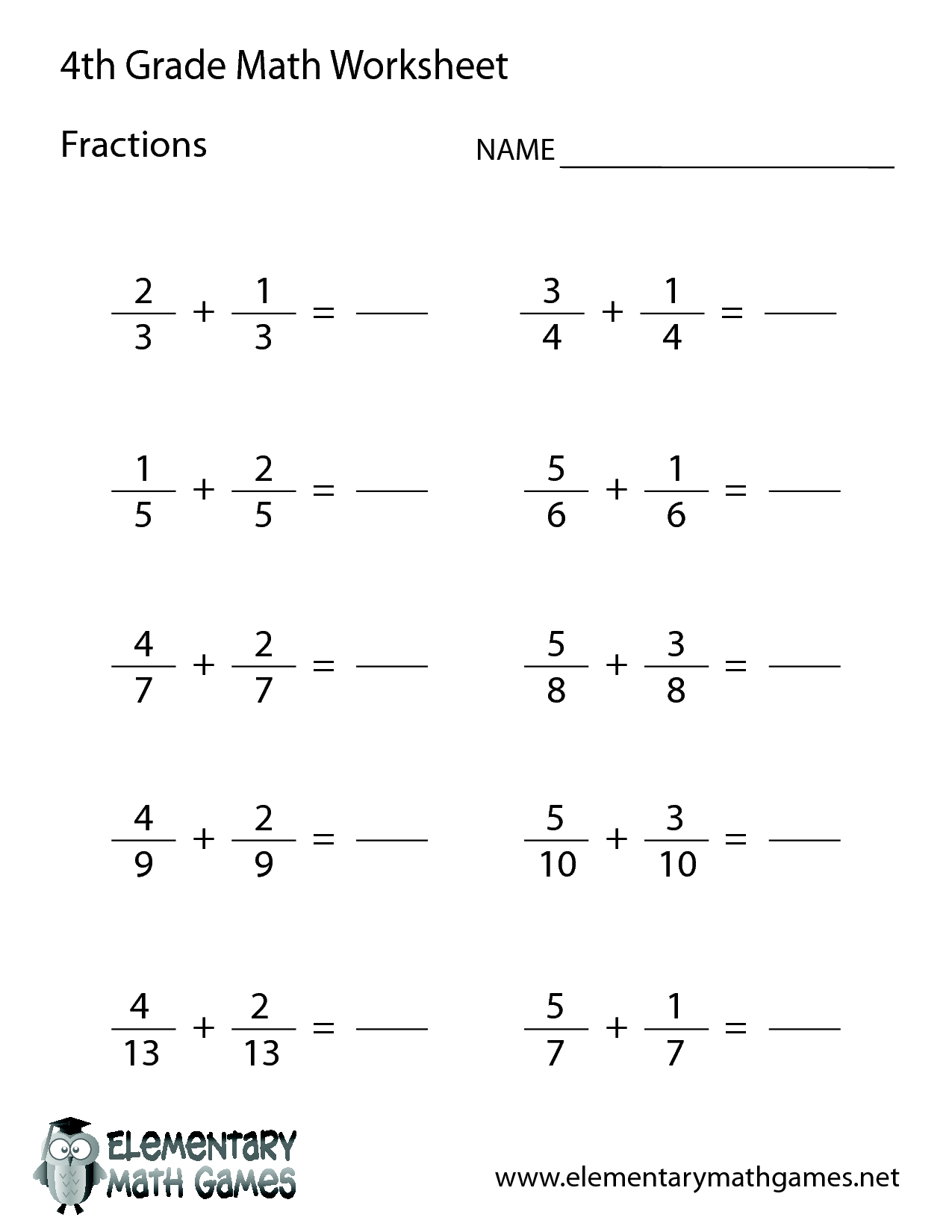
- 4th Grade Math Worksheets Fractions
- Math Fraction Worksheets
- 6th Grade Math Worksheets Rounding
- Money Addition Worksheets
- Long Division Worksheets 4th Grade
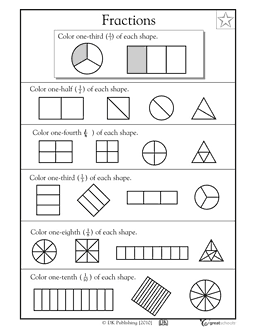
- Shape Fractions Worksheets Grade 1
- Kindergarten Math Addition Worksheets
- Subtraction with Regrouping Worksheets 3rd Grade
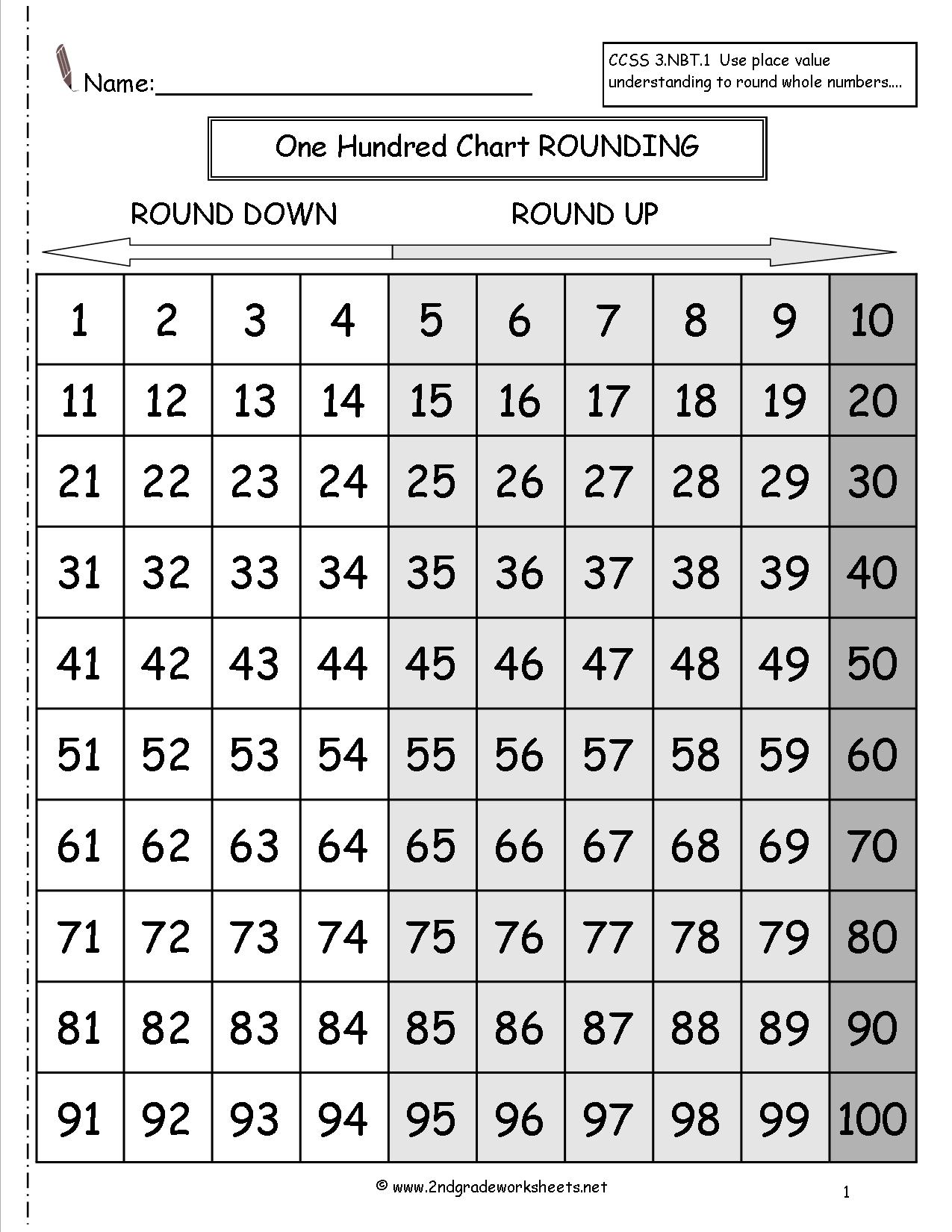
- Rounding Numbers Tens Ones Hundreds Charts
More Math Worksheets
Printable Math WorksheetsMath Worksheets Printable
Printable Math Worksheets Multiplication
Math Worksheets for 2nd Graders
Math Practice Worksheet Grade 6
Math Multiplication Worksheets
First Grade Subtraction Math Worksheets Printable
Math Worksheets Integers
Superhero Math Worksheets
Middle School Math Coloring Worksheets
What is the concept of counting and comparing numbers?
Counting involves determining the quantity of items in a set by assigning a number to each item, while comparing numbers involves evaluating the relative sizes of two or more numbers to determine which is larger or smaller. Counting helps establish the numerical value of a set, while comparing numbers aids in making comparisons between different quantities. Both concepts are fundamental mathematical skills that are used in various everyday activities and problem-solving situations.
How can fractions be represented and understood?
Fractions can be represented and understood as a way to describe parts of a whole or a group. They consist of a numerator (the top number) representing the number of parts being considered, and a denominator (the bottom number) representing the total number of parts that make up the whole. Fractions can be represented visually using diagrams like circles or rectangles divided into equal parts, or they can be converted into decimal numbers for easier calculation. Understanding fractions involves knowing how to compare, add, subtract, multiply, and divide them, as well as recognizing equivalent fractions that represent the same quantity in different ways. Practice and real-life examples help in gaining a better understanding of fractions and their applications.
What strategies can be used to solve addition and subtraction problems?
Strategies such as breaking numbers down into smaller, easier-to-manage parts, using number lines or manipulatives to visualize the problem, regrouping or borrowing when necessary, and practicing mental math techniques like counting on or back can be helpful when solving addition and subtraction problems. Additionally, using algorithms like the standard method or the "counting up" method can also aid in tackling these types of problems efficiently.
How can multiplication facts be memorized and applied?
Multiplication facts can be memorized and applied by regularly practicing and reviewing them, breaking them down into smaller, more manageable groups, using mnemonic devices or tricks to remember them, and applying them in real-life situations. Consistent practice, such as through flashcards or online games, can help reinforce the facts and improve recall. By understanding the patterns and relationships between numbers, individuals can become more adept at quickly recalling multiplication facts when needed.
What are the properties of geometric shapes?
Geometric shapes have various properties such as size, shape, dimensions, angles, lines, symmetry, and orientation. They can be categorized based on their sides, angles, and vertices. Additionally, geometric shapes have unique properties like area, perimeter, circumference, volume, and surface area that can be calculated using specific formulas depending on the shape. Each shape possesses specific characteristics that make it distinct and have applications in numerous fields like architecture, engineering, and mathematics.
How can measurement tools be used to determine length, weight, and capacity?
Measurement tools such as rulers, tape measures, scales, and measuring cups can be used to determine length, weight, and capacity by quantifying the dimensions of an object or substance. For determining length, tools like rulers and tape measures can be used to measure the distance from one point to another in units such as inches or centimeters. Weight can be determined using scales or balances, which measure the force exerted by an object due to gravity. Capacity, on the other hand, can be measured using measuring cups or containers that show volume in units such as ounces or milliliters, allowing for the determination of the amount of liquid or substance that can be held within the container.
What is the concept of probability and how can it be applied?
Probability is a measure of the likelihood of an event occurring, ranging from 0 (impossible) to 1 (certain). It is used to quantify uncertainty and make informed decision-making in various fields such as insurance, weather forecasting, finance, and gaming. By understanding probability, we can assess risks, predict outcomes, and make rational choices based on the likelihood of different events happening. It is a fundamental concept in statistics and mathematics that plays a crucial role in everyday life and decision-making processes.
How can data be organized and interpreted using charts and graphs?
Data can be organized and interpreted using charts and graphs by selecting the appropriate type of chart or graph that best represents the data, such as bar graphs, pie charts, or line graphs. The data is then inputted into the chosen chart or graph format, making it visually easier to understand patterns, trends, and relationships within the data. By presenting data in a visual format, it becomes easier to interpret and draw meaningful insights from the information, allowing for more informed decision-making and communication of key findings.
What strategies can be used to solve time and money word problems?
To solve time and money word problems, it is important to carefully read the problem and identify the key pieces of information such as the unknown quantity, the known quantities, and any relationships between them. Breaking down the problem into smaller, more manageable steps can be helpful. For time problems, converting all time units to a consistent format (e.g., minutes or hours) can simplify calculations. For money problems, setting up equations or representing the problem with a diagram can aid in visualizing the relationships between the different quantities. Additionally, using logic and common sense to cross-check calculations can help avoid mistakes.
How can patterns and sequences be identified and extended?
Patterns and sequences can be identified by observing the relationship between each term, whether it involves adding a constant, multiplying by a certain factor, or following a specific rule. To extend the pattern or sequence, one can use the identified relationship to predict and generate future terms by applying the same rule consistently. It is essential to look for recurring patterns and rules within the sequence to effectively extend it.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.













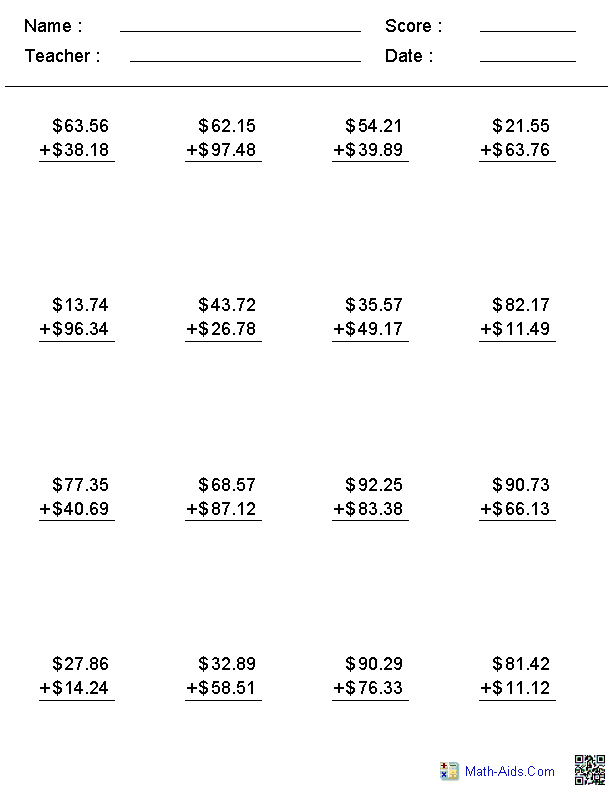

















Comments