Linear Equations with Fractions Worksheet
Linear equations with fractions can be challenging for many students. Understanding how to solve these types of equations requires a solid understanding of both the mathematical properties of fractions and how to manipulate equations using variables. If you're a student who needs practice in this area or a teacher looking for a resource to support your lessons, this Linear Equations with Fractions Worksheet is a valuable tool to help solidify your understanding of this topic.
Table of Images 👆
- One Step Equations Worksheets
- Fraction Equation Worksheets with Variables
- Simple-Interest 7th Grade Math Worksheets
- Algebra 1 Step Equation Problems Worksheets
- Algebra Equations Word Problems Worksheets
- Lowest Term Fraction Worksheet
- Subtracting Rational Expressions Worksheet
- Solving System Linear Equations Algebraically Worksheet
- Simplifying Expressions Worksheets 7th Grade
- Middle School Math Word Problems
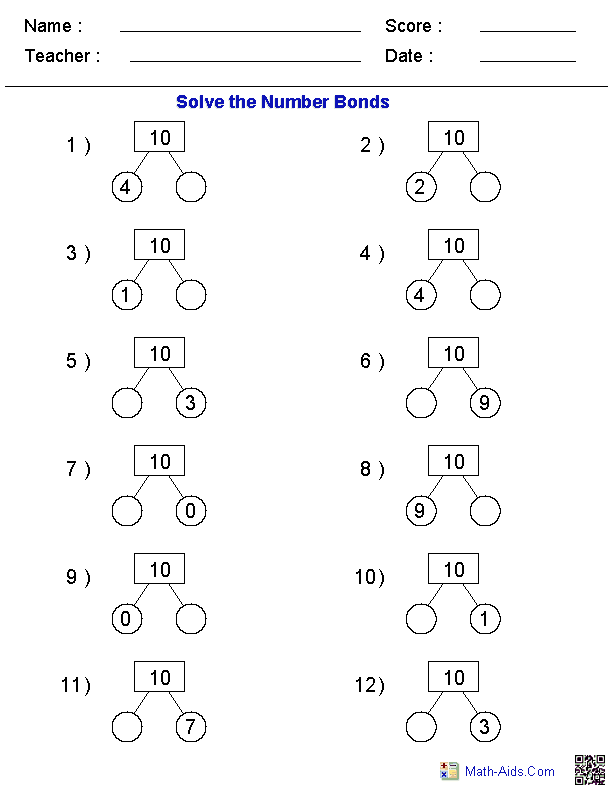
- Number Bonds Worksheets
- Evaluating Algebra Expressions Worksheets
- Algebra 1 Worksheets
- 7th Grade Math Word Problems
- Math Division Worksheets 3rd Grade
- Math Division Worksheets 3rd Grade
- Math Division Worksheets 3rd Grade
More Line Worksheets
Lines of Symmetry WorksheetsLine Drawing Art Worksheets
Drawing Contour Lines Worksheet
Contour Lines Topographic Map Worksheets
Rosa Parks Timeline Worksheet
Blank Printable Timeline Worksheets
2 Lines of Symmetry Worksheets
Linear Equations Worksheet 7th Grade
Rounding Decimals Number Line Worksheet
Graphing Inequalities On a Number Line Worksheets
Write the equation of a line in slope-intercept form using fractions.
To write the equation of a line in slope-intercept form using fractions, you would write it as y = mx + b, where m is the slope of the line (a fraction like 3/5, for example) and b is the y-intercept (a fraction like 1/4, for example). So, an example of a line in slope-intercept form with fractions could be y = (3/5)x + (1/4).
Solve the equation: (3/4)x - 5 = 2/3.
To solve the equation (3/4)x - 5 = 2/3, first isolate the variable x. Add 5 to both sides of the equation to get (3/4)x = 2/3 + 5. Then find a common denominator to add 2/3 and 5, which is 15. Therefore, 2/3 + 5 = 2/3 + 15/3 = 17/3. So now the equation becomes (3/4)x = 17/3. To solve for x, multiply both sides by the reciprocal of (3/4), which is 4/3. This gives x = (17/3) * (4/3) = 68/9, or x = 7.56 (rounded to two decimal places). Thus, the solution to the equation is x = 68/9 or x ≈ 7.56.
Find the solution to the system of equations: 2x/3 + 1/2y = 5/6 and x/5 - y/4 = 7/10.
The solution to the system of equations is x = 2, y = 4.
Graph the linear equation: y = -2/5x + 3.
To graph the linear equation y = -2/5x + 3, start by plotting the y-intercept at 3 on the y-axis. Then, use the slope of -2/5 to find a second point by moving down 2 units and to the right 5 units, and plot that point. Connect the two points to draw a straight line. This line represents the graph of the linear equation y = -2/5x + 3.
Simplify the expression: (2/3)(3/8) - (1/4)(5/6).
To simplify the expression (2/3)(3/8) - (1/4)(5/6), we first multiply the fractions within the parentheses: (2/3)(3/8) = 6/24 and (1/4)(5/6) = 5/24. Subtracting these two results gives 6/24 - 5/24 = 1/24. Therefore, the simplified expression is 1/24.
Solve for x: (4/5)(2x - 1) = 3/4.
To solve for x, first distribute the 4/5 on the left side, giving you (8/5)x - 4/5 = 3/4. Then, add 4/5 to both sides to isolate the x term, resulting in (8/5)x = 3/4 + 4/5. Now, find a common denominator to add the fractions on the right side, which would be 20, so 3/4 + 4/5 = 15/20 + 16/20 = 31/20. Finally, multiply both sides by 5/8 to solve for x, leading to x = (31/20) * 5/8 = 31/32. Thus, the solution for x is 31/32.
Determine the slope of the line passing through the points (-3, 1) and (2, -4) using fractions.
To determine the slope of the line passing through the points (-3, 1) and (2, -4) using fractions, we use the formula for slope which is (y2 - y1) / (x2 - x1). By substituting the coordinates of the points into the formula, we get (-4 - 1) / (2 - (-3)) = -5 / 5 = -1. Therefore, the slope of the line passing through the points (-3, 1) and (2, -4) is -1.
Rewrite the equation 2x - 3y = 7 in slope-intercept form.
To rewrite the equation 2x - 3y = 7 in slope-intercept form, we need to solve for y. By isolating y, we get y = (2/3)x - 7/3. Therefore, the equation in slope-intercept form is y = (2/3)x - 7/3.
Solve the inequality: (1/2)x + (3/4) > 1/3.
To solve the inequality (1/2)x + (3/4) > 1/3, first simplify the left side by finding a common denominator, giving us (2/4)x + (3/4) > 1/3. Combining the fractions, we get (5/4)x > 1/3. Multiplying both sides by (4/5) to isolate x, we have x > 4/15. Therefore, the solution to the inequality is x > 4/15.
Find the x-intercept of the line represented by the equation 2/3x - 4y = 8.
To find the x-intercept of the line represented by the equation 2/3x - 4y = 8, we need to substitute y with 0 in the equation. This gives us 2/3x - 4(0) = 8, simplifying to 2/3x = 8. Solving for x, we get x = 12. Therefore, the x-intercept of the line is 12.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.













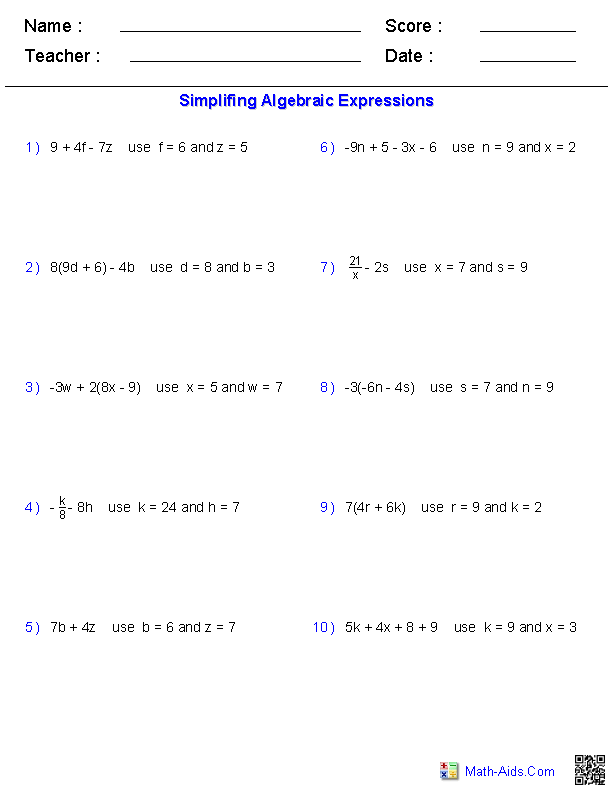


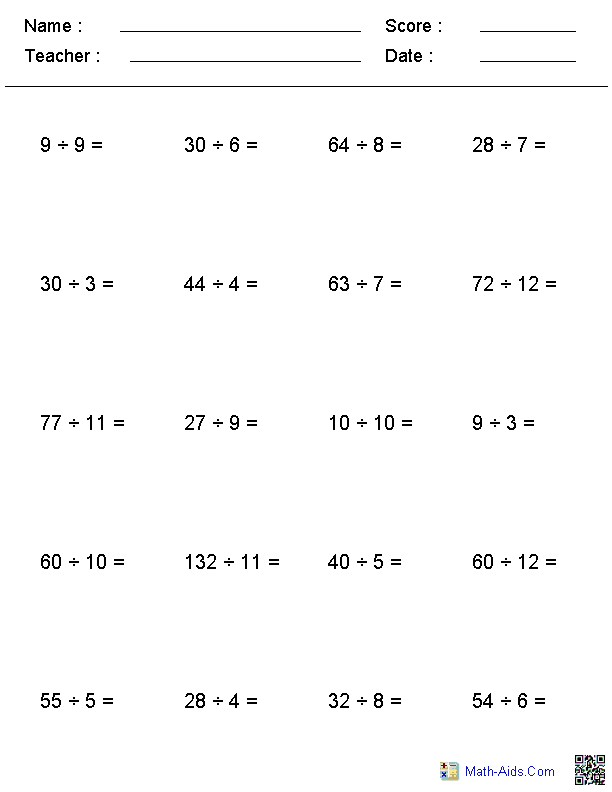
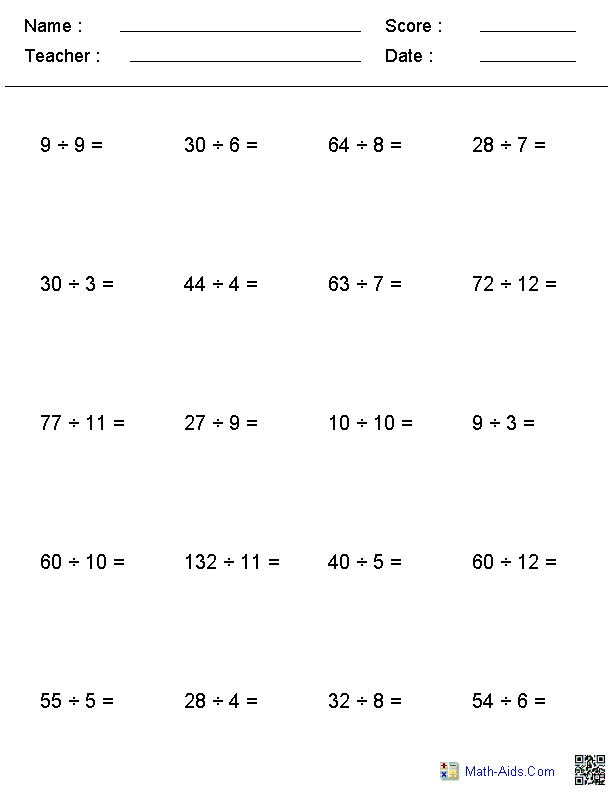














Comments