Laws of Exponents Worksheet
Are you a math enthusiast or a student looking for a reliable resource to practice and reinforce your understanding of the laws of exponents? Look no further! In this blog post, we will explore the benefits of using worksheets specifically designed to help you master this fundamental mathematical concept. Whether you're studying for a test, seeking additional practice, or simply want to solidify your knowledge, worksheets are an excellent tool for self-assessment and skill development. So, let's dive in and see why worksheets can be a valuable asset in your learning journey.
Table of Images 👆
- Exponents Worksheets 6th-Grade
- Multiplication Exponents Worksheet Answers
- Simplifying Expressions Worksheets 6th Grade
- Exponent Worksheets with Integers
- Substitution Method Worksheet
- Evaluate Expressions Involving Exponents
- Printable Math Addition Worksheets
- Numerical Expressions with Exponents
- Algebra Tiles Solving Equations Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is the product rule?
The product rule is a formula used in calculus to find the derivative of the product of two functions. It states that the derivative of the product of two functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function. Mathematically, if f(x) and g(x) are two functions, then the derivative of their product, f(x)g(x), is given by (f'(x)g(x)) + (f(x)g'(x)).
What is the quotient rule?
The quotient rule is a formula used in calculus for finding the derivative of a function that is the quotient of two other functions. It states that the derivative of f(x)/g(x) is equal to (g(x)*f'(x) - f(x)*g'(x))/(g(x))^2, where f(x) and g(x) are functions and f'(x) and g'(x) are their respective derivatives.
What is the power rule?
The power rule states that the derivative of a term in the form of x^n, where n is a constant, is equal to n times x^(n-1). In simpler terms, it gives a formula for finding the derivative of a term with an exponent by bringing down the exponent as a coefficient and reducing the exponent by one.
What is the zero exponent rule?
The zero exponent rule states that any non-zero number raised to the power of zero is equal to 1. In other words, for any non-zero number "a," a^0 = 1. This rule applies to both positive and negative numbers.
How do you simplify expressions with negative exponents?
To simplify expressions with negative exponents, you can move the term with the negative exponent to the denominator and change the negative exponent to a positive exponent. For example, if you have x^-2, you can rewrite it as 1/x^2. This allows you to simplify the expression by making the exponent positive and moving the term to the appropriate location in the expression.
How do you simplify expressions with fractional exponents?
To simplify expressions with fractional exponents, you can use the rule that a fractional exponent represents a root. For example, x^(1/2) represents the square root of x, x^(1/3) represents the cube root of x, and so on. You can simplify expressions by rewriting them using the appropriate root. Additionally, you can use properties of exponents, such as multiplying exponents of the same base or dividing exponents of the same base, to simplify further. By applying these rules and properties, you can simplify expressions with fractional exponents to their simplest form.
What is the rule for multiplying exponents with the same base?
The rule for multiplying exponents with the same base is to add the exponents together. For example, if you have x^a * x^b, where a and b are exponents and x is the base, you would simplify it by adding the exponents: x^(a+b).
What is the rule for dividing exponents with the same base?
When dividing exponents with the same base, you subtract the exponent in the denominator from the exponent in the numerator. This means that if you have x^m / x^n, where x is the base, the result is x^(m-n).
How do you simplify expressions with multiple exponents?
To simplify expressions with multiple exponents, you should apply the rules of exponents. Start by combining like terms and multiplying the coefficients. Then, use the properties of exponents to simplify the terms with similar bases. Add or subtract the exponents depending on whether the terms are multiplied or divided. Finally, simplify further by performing any necessary operations such as additions, subtractions, multiplications, or divisions. Remember to follow the order of operations and keep track of the rules of exponents to simplify the expression efficiently.
How do you simplify expressions with variables and exponents?
To simplify expressions with variables and exponents, you can use the rules of exponents. Combine like terms by adding or subtracting coefficients, and multiply or divide coefficients with the same base if the exponents are being added or subtracted. Remember to follow the order of operations (PEMDAS) when simplifying expressions with variables and exponents to ensure accuracy. It is also helpful to look for common factors or terms that can be factored out to simplify the expression further.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.







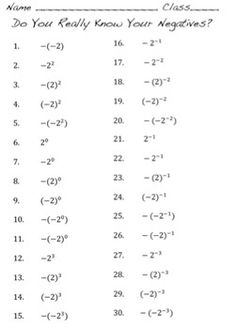


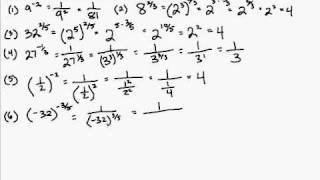














Comments