Law of Cosines Worksheet Answers

Are you a high school math student or educator searching for reliable Law of Cosines worksheet answers? Look no further, as this blog post provides an extensive collection of solutions to help you enhance your understanding of this important trigonometric concept. Whether you're practicing for an upcoming test or looking for supplementary material to reinforce your knowledge, our carefully crafted answers ensure that you have the necessary resources to succeed.

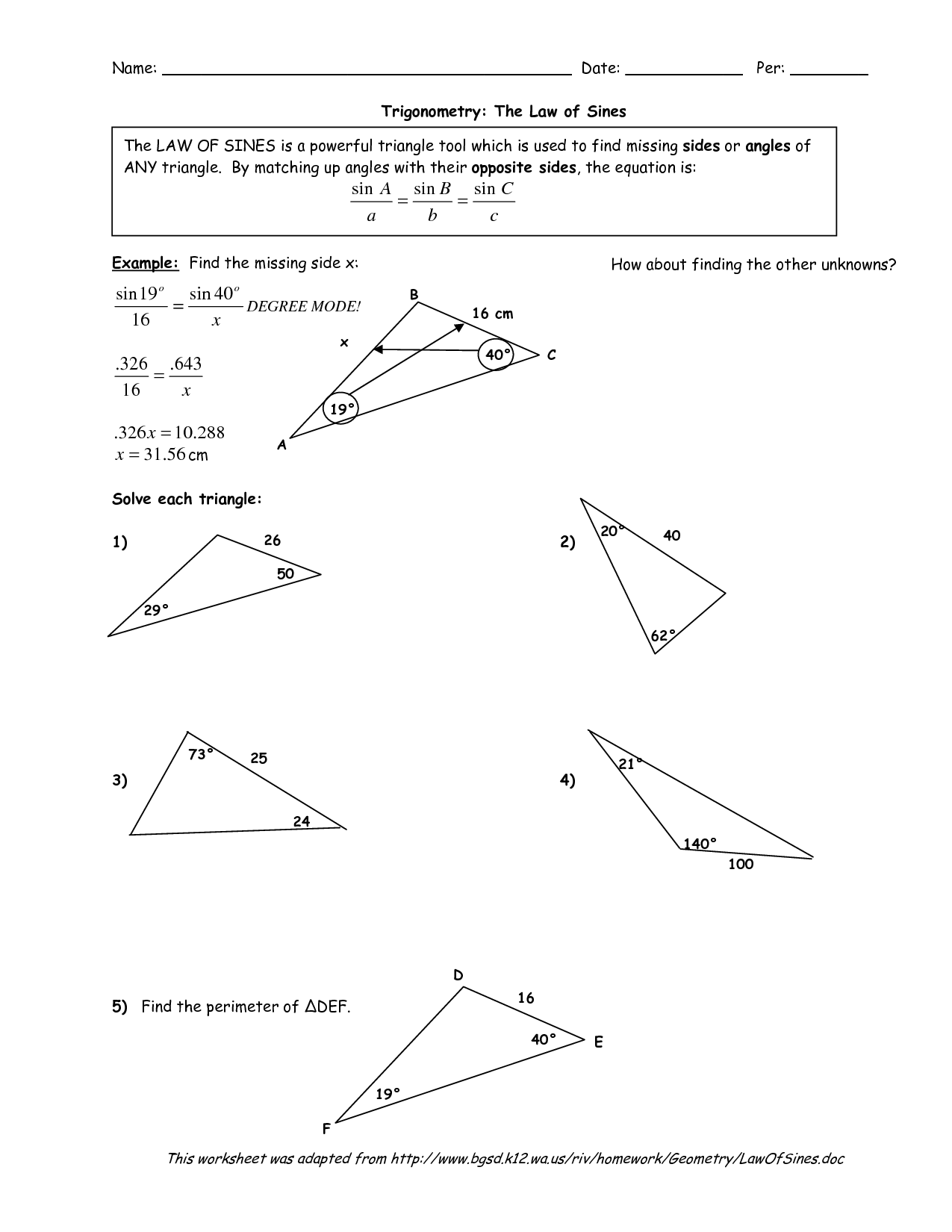
  Law of Sine Trigonometric Functions

---

  Law of Sines and Cosines Worksheet

---

  Geometry Chapter 7 Review Answers

---

  Law of Sines and Cosines Worksheet

---

  Law of Sines and Cosines Worksheet

---

  The Law of Sines Kuta Software Infinite Algebra Answer Key

---

  Law of Sines and Cosines Worksheet

---

  Sine Cosine and Tangent Worksheets

---

  Law of Sines and Cosines Worksheet

---

  Momentum Word Problems Worksheet Answers

---

  Law of Sines and Cosines Worksheet

---

What is the Law of Cosines?

The Law of Cosines is a trigonometric formula that relates the lengths of the sides of a triangle to the cosine of one of its angles. It states that the square of a side of a triangle is equal to the sum of the squares of the other two sides, minus twice the product of those sides and the cosine of the included angle. This law is particularly useful in solving for unknown sides or angles in non-right triangles.

When do we use the Law of Cosines?

The Law of Cosines is used in trigonometry to find the unknown side lengths or angles of a triangle when the lengths of two sides and the included angle are known, or when the lengths of all three sides are known. It is particularly useful for solving triangles that are not right triangles.

How is the Law of Cosines different from the Pythagorean Theorem?

The Law of Cosines is a generalization of the Pythagorean Theorem, used to solve triangles with non-right angles. The Pythagorean Theorem only applies to right triangles and states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. In contrast, the Law of Cosines applies to any triangle and relates the lengths of all three sides to the cosine of one of its angles. The Law of Cosines is a more versatile tool for solving triangles in general, while the Pythagorean Theorem is specific to right triangles.

What is the formula for the Law of Cosines?

The formula for the Law of Cosines is c^2 = a^2 + b^2 - 2ab * cos(C), where c is the side opposite the angle C, and a and b are the lengths of the other two sides of a triangle.

How do we use the Law of Cosines to find the length of a side in a triangle?

To use the Law of Cosines to find the length of a side in a triangle, you can use the formula: \( a^2 = b^2 + c^2 - 2bc \cdot \cos(A) \), where 'a' is the side whose length you are trying to find, 'b' and 'c' are the other two sides of the triangle, and 'A' is the angle opposite side 'a'. Simply plug in the values of the known sides and angles into the formula, solve for the unknown side length.

How do we use the Law of Cosines to find the measure of an angle in a triangle?

To use the Law of Cosines to find the measure of an angle in a triangle, you can rearrange the formula to solve for the angle. Specifically, you can use the formula cos(A) = (b^2 + c^2 - a^2) / (2bc) where A is the angle you want to find, and a, b, and c are the side lengths of the triangle opposite to angles A, B, and C respectively. By rearranging this formula, you can solve for the angle A using the given side lengths of the triangle.

Can the Law of Cosines be used for any triangle?

Yes, the Law of Cosines can be used for any triangle, regardless of its type (acute, right, obtuse). It is a generalization of the Pythagorean theorem and can be applied to find the lengths of the sides or angles of a triangle when the lengths of other sides and included angles are known.

How is the Law of Cosines related to the Law of Sines?

The Law of Cosines and the Law of Sines are both trigonometric formulas used to solve triangles, but they are applicable in different scenarios. The Law of Cosines is used to find the length of a side of a triangle when all three sides or two sides and the included angle are known, while the Law of Sines is used to find unknown angles or sides in a triangle when some angles and sides are known. The Law of Cosines can be seen as a more general and versatile formula than the Law of Sines, as it can be used to solve triangles that do not involve a right angle, unlike the Law of Sines.

Can the Law of Cosines be used to solve real-life problems?

Yes, the Law of Cosines can be applied to real-life problems involving distances, angles, and sides in non-right-angled triangles. It is commonly used in fields such as engineering, physics, navigation, and surveying to determine unknown sides or angles in a triangle when the lengths of other sides and angles are known. By using the Law of Cosines, one can calculate distances between objects, positions of points, or bearings in various practical situations.

What are some common applications of the Law of Cosines in various fields?

The Law of Cosines is commonly used in fields such as trigonometry, geometry, physics, engineering, and astronomy. In surveying and navigation, it is used to determine distances and angles between objects or positions. In mechanical engineering, it is used in analyzing forces and stresses in structures. In astronomy, it helps calculate distances between celestial objects. In physics, it is used in vector analysis and to solve problems involving displacement, velocity, and acceleration. Overall, the Law of Cosines is a fundamental tool in various fields that involve the measurement of angles and distances.