Introduction Algebra Worksheet
Algebra worksheets provide a valuable opportunity for students to practice and reinforce their understanding of important mathematical concepts. These worksheets offer a structured and organized way to engage with algebraic equations and problems, making it easier for learners to grasp the subject matter. Whether you are a student seeking extra practice or a teacher looking for additional resources to support your lessons, algebra worksheets can be a helpful tool for enhancing math skills.
Table of Images 👆
- Free Printable Algebra 1 Worksheets
- Unit 5 Review Algebra 1 Worksheet
- Algebra 1 Practice Test
- Algebra 1 Simplifying Expressions Worksheet
- Equation Worksheets
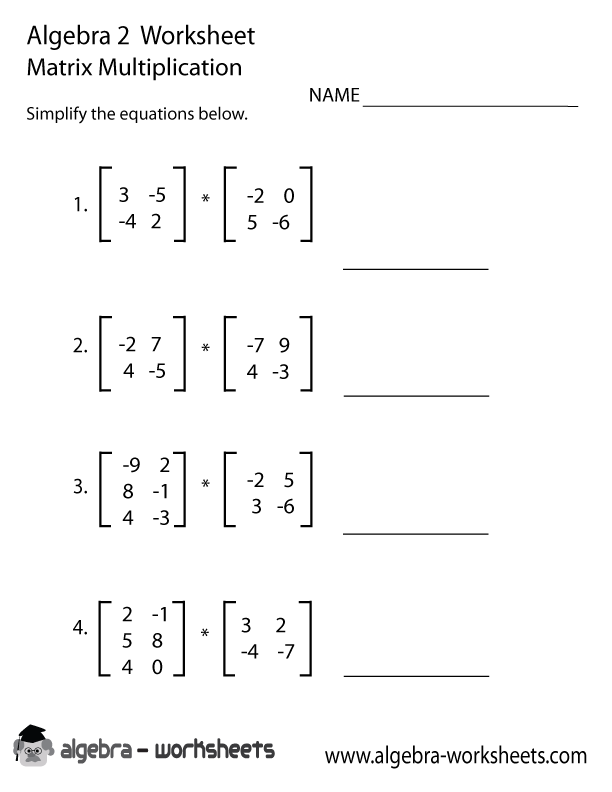
- Printable Matrix Worksheets
- Factoring Quadratic Expressions Worksheet
- Equality Property of Addition Worksheets
- College Algebra Worksheets
- Introduction Multiplication Worksheets
- College Algebra Practice Test Worksheets
- Algebraic Expressions Worksheets
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the goal of Introduction Algebra?
The goal of Introduction Algebra is to provide students with a foundational understanding of algebraic concepts and operations, including equations, variables, and functions. By mastering these fundamental building blocks of mathematics, students can develop problem-solving skills and critical thinking abilities that are essential for success in more advanced mathematical concepts and real-world applications.
What are the main topics covered in the worksheet?
The main topics covered in the worksheet include arithmetic operations, fractions, geometry concepts, measurement conversions, and word problems related to real-life scenarios.
How does Introduction Algebra relate to other branches of mathematics?
Introduction to algebra is a fundamental concept that forms the basis for higher-level mathematical branches such as calculus, geometry, number theory, and linear algebra. Algebra provides the essential tools and techniques for solving equations, manipulating expressions, and understanding the relationships between variables. These skills are crucial in various mathematical fields and are used extensively to model real-world problems, proving the importance of algebra as a prerequisite for advancing in the study of mathematics.
What are the basic operations in algebra?
The basic operations in algebra are addition, subtraction, multiplication, and division. These operations are used to manipulate variables, constants, and equations to solve for unknowns, simplify expressions, and solve equations.
How do variables and constants differ in algebra?
In algebra, variables are unknown values that can change, represented by letters such as x or y, while constants are fixed values with a specific, unchanging numerical value. Variables can represent different values in an equation or expression, while constants always have the same value and do not change.
What are equations and inequalities, and how are they used in algebra?
Equations are mathematical expressions stating that two quantities are equal, while inequalities compare two quantities, showing a relationship that one is greater than, less than, or not equal to the other. In algebra, equations and inequalities are used to solve for unknown variables by manipulating the given expressions using various operations such as addition, subtraction, multiplication, and division. They help in solving real-world problems, finding solutions to mathematical questions, and understanding relationships between variables in a system of equations or inequalities.
What is the process of simplifying algebraic expressions?
To simplify algebraic expressions, you typically combine like terms, perform operations within parentheses, and apply rules of exponents or factor out common factors. This involves following the order of operations (PEMDAS) and applying distributive property when necessary. Grouping like terms helps to condense the expression and make it easier to work with while keeping the overall value unchanged.
How are exponents and radicals used in algebraic equations?
Exponents and radicals are used in algebraic equations to represent numbers or variables raised to a certain power. Exponents indicate how many times a number or variable is multiplied by itself, while radicals represent the inverse operation of taking a root. Both exponents and radicals are used to simplify expressions, solve equations, and manipulate terms within algebraic equations to make calculations more efficient and manageable.
What are the properties and rules that govern algebraic manipulations?
The properties and rules that govern algebraic manipulations include the commutative property (a + b = b + a), the associative property ((a + b) + c = a + (b + c)), the distributive property (a(b + c) = ab + ac), the additive identity (a + 0 = a), the multiplicative identity (a * 1 = a), and the multiplicative property of zero (a * 0 = 0). Additionally, rules such as combining like terms, simplifying expressions, and solving equations by isolating variables are fundamental in algebraic manipulations.
How is algebra applied in real-life situations and other academic fields?
Algebra is applied in real-life situations such as budgeting, calculating interest rates, analyzing trends in data, and solving various types of equations in fields like engineering, science, economics, and computer programming. Additionally, algebra is fundamental in other academic fields such as physics, chemistry, and statistics for solving problems, making predictions, and understanding complex relationships between different variables.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.








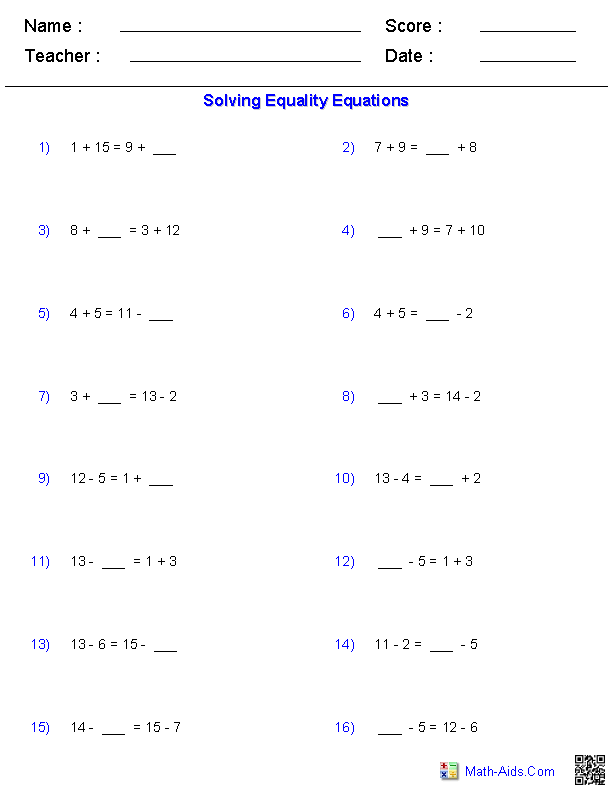




















Comments