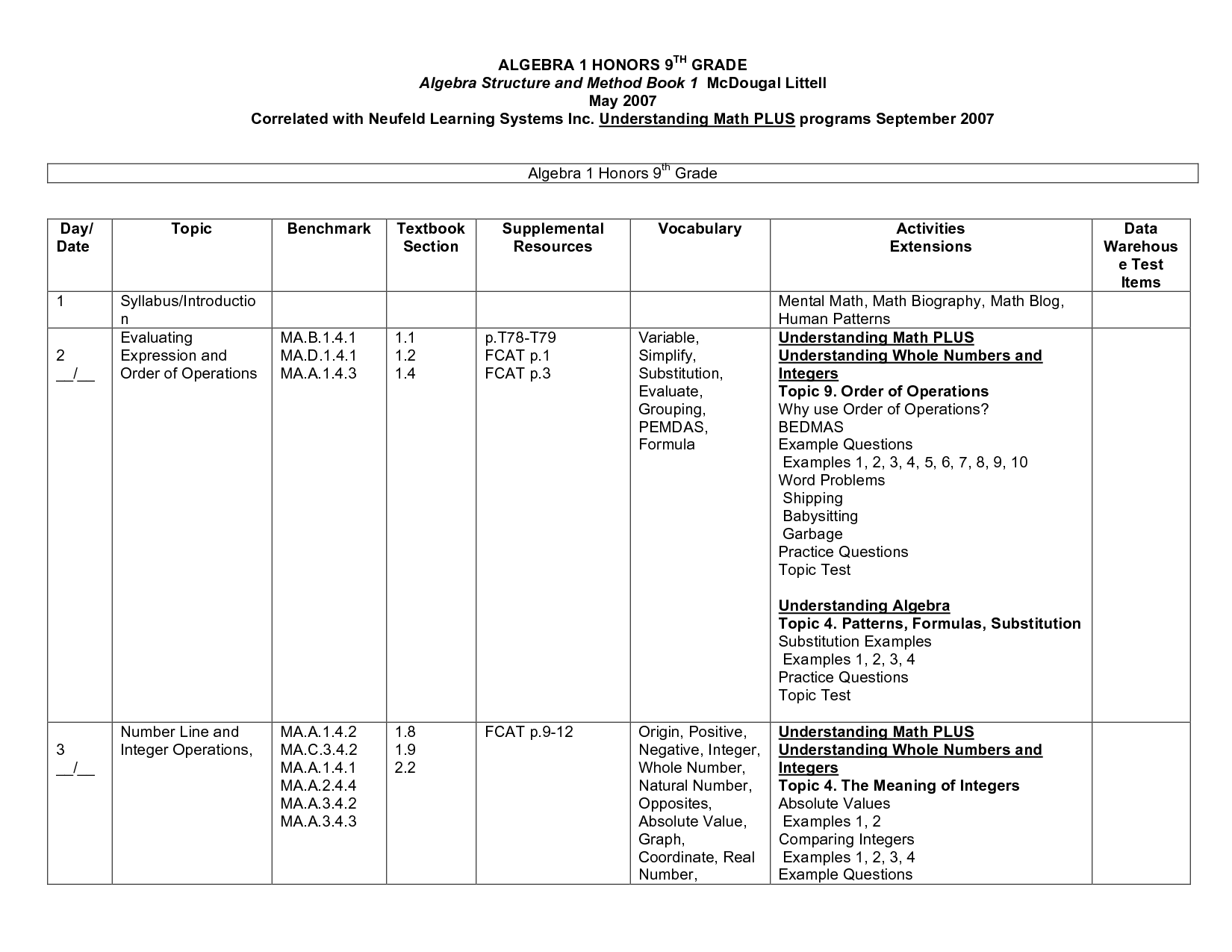
Honors Algebra 2 Worksheets

Honors Algebra 2 worksheets provide a valuable resource for high school students enrolled in advanced mathematics courses. These worksheets offer a wide range of exercises and problems that cover the curriculum extensively, allowing students to practice and reinforce their understanding of complex algebraic concepts. Whether you are a teacher seeking additional materials for your classroom or a student looking to improve your skills, Honors Algebra 2 worksheets offer a comprehensive way to engage with the subject matter.

  Logarithmic Equations Worksheet

---

  Algebra 1 Worksheets 9th Grade Math

---

  Linear Programming Worksheet and Answers

---

  Linear Programming Worksheet

---

  Algebra 2 and Trigonometry Worksheets

---

  The New Testament

---

  Algebra 1 Worksheets Chapter 8

---

  Algebra 1 Worksheets

---

What are the main topics covered in Honors Algebra 2 worksheets?

The main topics covered in Honors Algebra 2 worksheets typically include advanced concepts such as functions, quadratic equations, exponential and logarithmic functions, complex numbers, systems of equations and inequalities, conic sections, sequences and series, probability and statistics, and matrices. Students are often required to solve complex problems, apply critical thinking skills, and demonstrate a deep understanding of algebraic concepts at a more challenging level compared to standard Algebra 2 courses.

How do you solve quadratic equations using different methods?

There are several methods to solve quadratic equations, including factoring, using the quadratic formula, completing the square, and graphing. Factoring involves breaking down the quadratic equation into two linear factors, while the quadratic formula (-b ± ?(b^2 - 4ac)) / 2a can be used for any quadratic equation in the form ax^2 + bx + c = 0. Completing the square involves transforming the quadratic equation into a perfect square trinomial, and graphing can be used to find the x-intercepts of the quadratic function. Each method has its own advantages and can be chosen based on the complexity of the equation and personal preference.

Describe the process of factoring quadratic expressions.

Factoring quadratic expressions involves rewriting the quadratic equation in the form of two binomials multiplied together. This is done by finding two numbers that multiply to the constant term of the quadratic expression and add up to the coefficient of the linear term. Once these numbers are found, they are used to rewrite the middle term of the quadratic expression as the sum of two terms which can then be factored. Finally, the quadratic expression is factored into the form (x + a)(x + b), where a and b are the constants found during the factoring process.

Explain the concept of complex numbers and how they are used in algebraic operations.

Complex numbers are numbers that consist of a real part and an imaginary part expressed in the form of a + bi, where "a" is the real part, "b" is the imaginary part, and "i" is the imaginary unit equal to the square root of -1. In algebraic operations, complex numbers are used to solve equations that do not have real solutions, such as finding the roots of quadratic equations with negative discriminants. Addition, subtraction, multiplication, and division of complex numbers are performed by treating the real and imaginary parts separately to simplify expressions and solve equations in algebraic manipulations. Additionally, complex numbers are widely used in various fields of mathematics, physics, engineering, and other sciences to model and solve real-world problems.

What are the steps for graphing linear equations on the coordinate plane?

To graph a linear equation on the coordinate plane, first identify the y-intercept by locating the point where the line crosses the y-axis. Then, use the slope of the line to find additional points by moving up or down on the y-axis and right or left on the x-axis based on the numerator and denominator of the slope. Connect the points to form a straight line that represents the equation. Remember to label the axes and any points on the line to ensure clarity and accuracy in the graph.

Describe the properties and applications of exponential functions.

Exponential functions represent mathematical relationships where the input variable is an exponent. They have the general form f(x) = a^x, where 'a' is a positive constant, and they grow or decay rapidly depending on the value of 'a'. Exponential functions are commonly used to model scenarios involving rapid growth or decay, such as population growth, radioactive decay, compound interest, and exponential growth in technology. They are also used in science, engineering, and finance to describe phenomena where the rate of change is proportional to the current value.

How do you solve systems of linear equations using the substitution method?

To solve systems of linear equations using the substitution method, you first solve one of the equations for one variable in terms of the other variable. Then you substitute this expression back into the other equation. By substituting the value of the variable, you can find the value of the other variable. Once you have the value of one variable, you can substitute it back into one of the original equations to find the value of the other variable, giving you the solution to the system of equations.

Explain the concept of logarithms and their relationship to exponential functions.

Logarithms are the inverse operations of exponential functions. In essence, logarithms answer the question "to what power must a base number be raised to obtain a given number?" Logarithms allow us to solve for the exponent when we know the base and the result of an exponential operation. They are denoted as log(base) = exponent. The logarithmic function is the inverse of the exponential function, as they undo each other's operations. This relationship is key in various mathematical and scientific applications.

Describe how to solve rational equations by finding a common denominator.

To solve rational equations by finding a common denominator, first factor the denominators and identify the least common multiple of all the factors. Then, multiply each term in the equation by the appropriate factors to clear the fractions and solve the resulting equation. Once you have solved for the variable, remember to check your solution to ensure it does not create any additional denominators that are equal to zero. If it does, those values are extraneous and should be excluded from the final solution.

What are the key principles of trigonometry and how are they applied in solving triangles?

The key principles of trigonometry involve the study of relationships between the angles and sides of triangles. These principles include the sine, cosine, and tangent functions, which relate the angles of a triangle to the lengths of its sides. In solving triangles, these trigonometric functions are used to find missing angles or side lengths by setting up and solving equations based on the given information. The Law of Sines and the Law of Cosines are also important principles in solving triangles, providing alternative methods for finding angles and side lengths in different types of triangles. These principles are applied in various real-world scenarios, such as in navigation, engineering, and physics, where the measurements and relationships of triangles are critical for solving problems.