High School Linear Equations Worksheets

If you're a high school student or teacher looking for a comprehensive resource to practice linear equations, you've come to the right place. Our collection of high school linear equations worksheets offers a range of exercises and problems that cover various aspects of the topic.

  High School Algebra Worksheets

---

  Multiplicative Inverse Property Worksheet

---

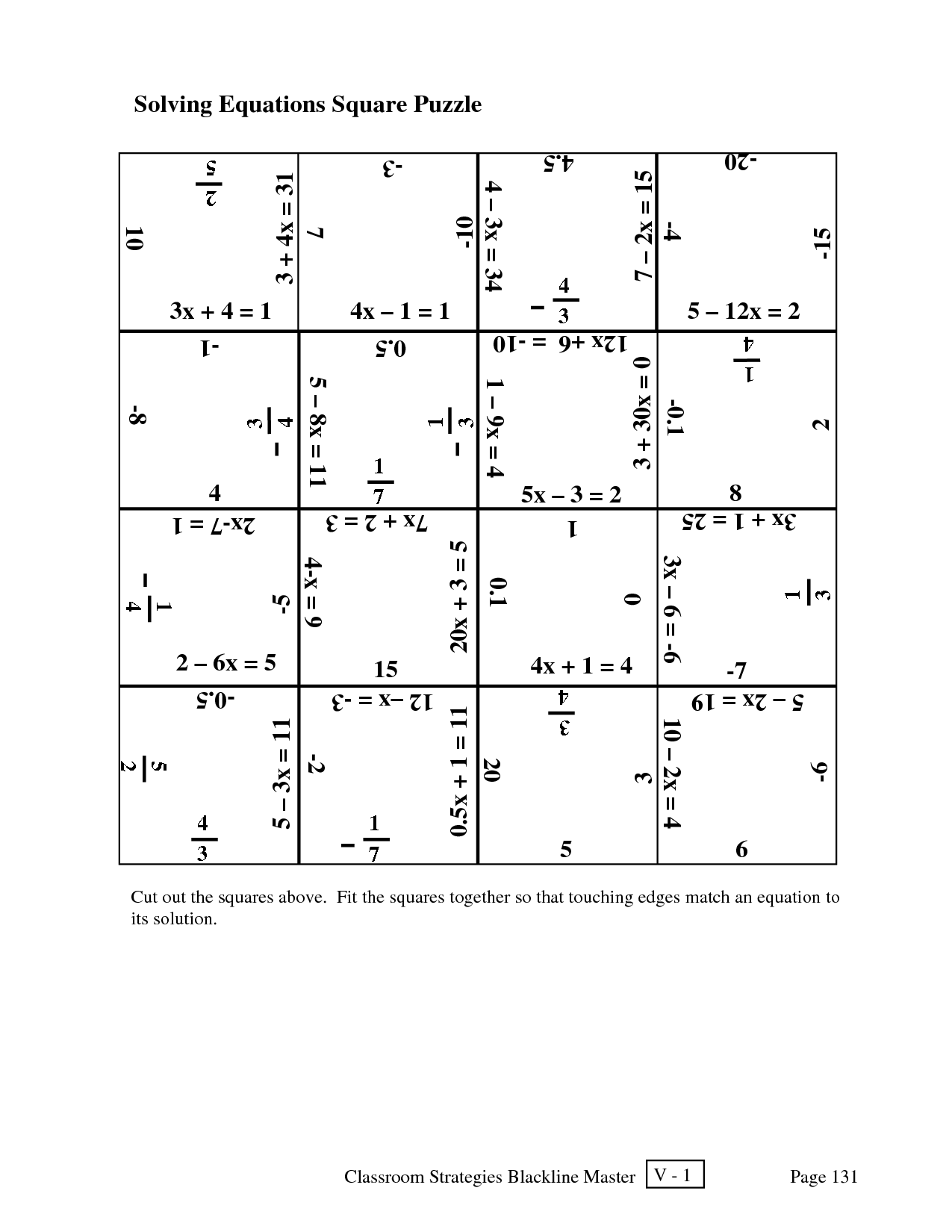
  Solving Equations Square Puzzle

---

  6th-Grade Frequency Table Worksheets

---

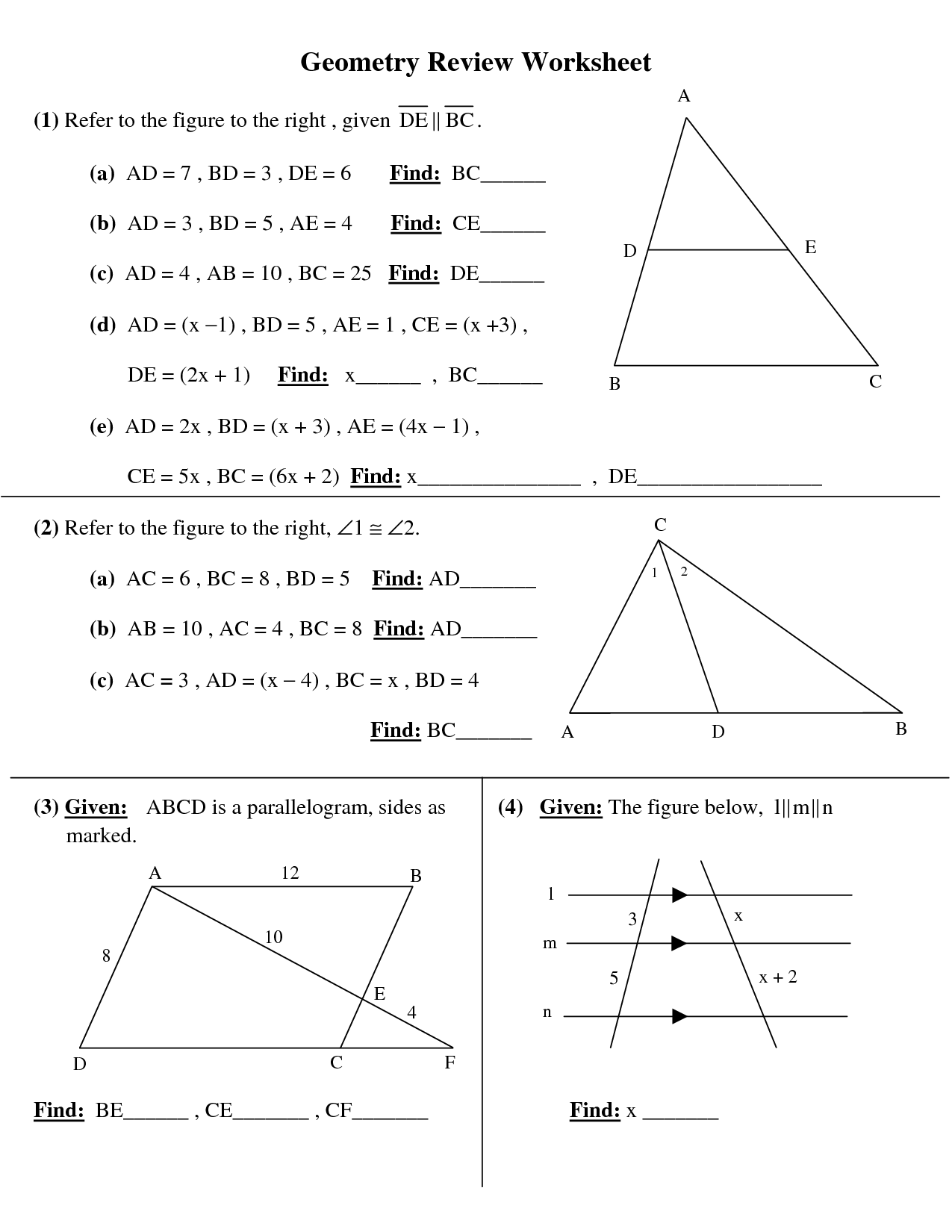
  High School Geometry Worksheets

---

  Who AM I Worksheet Activities

---

  Subtracting Integers Worksheets 7th Grade

---

  Simple Equations with Variables Worksheets

---

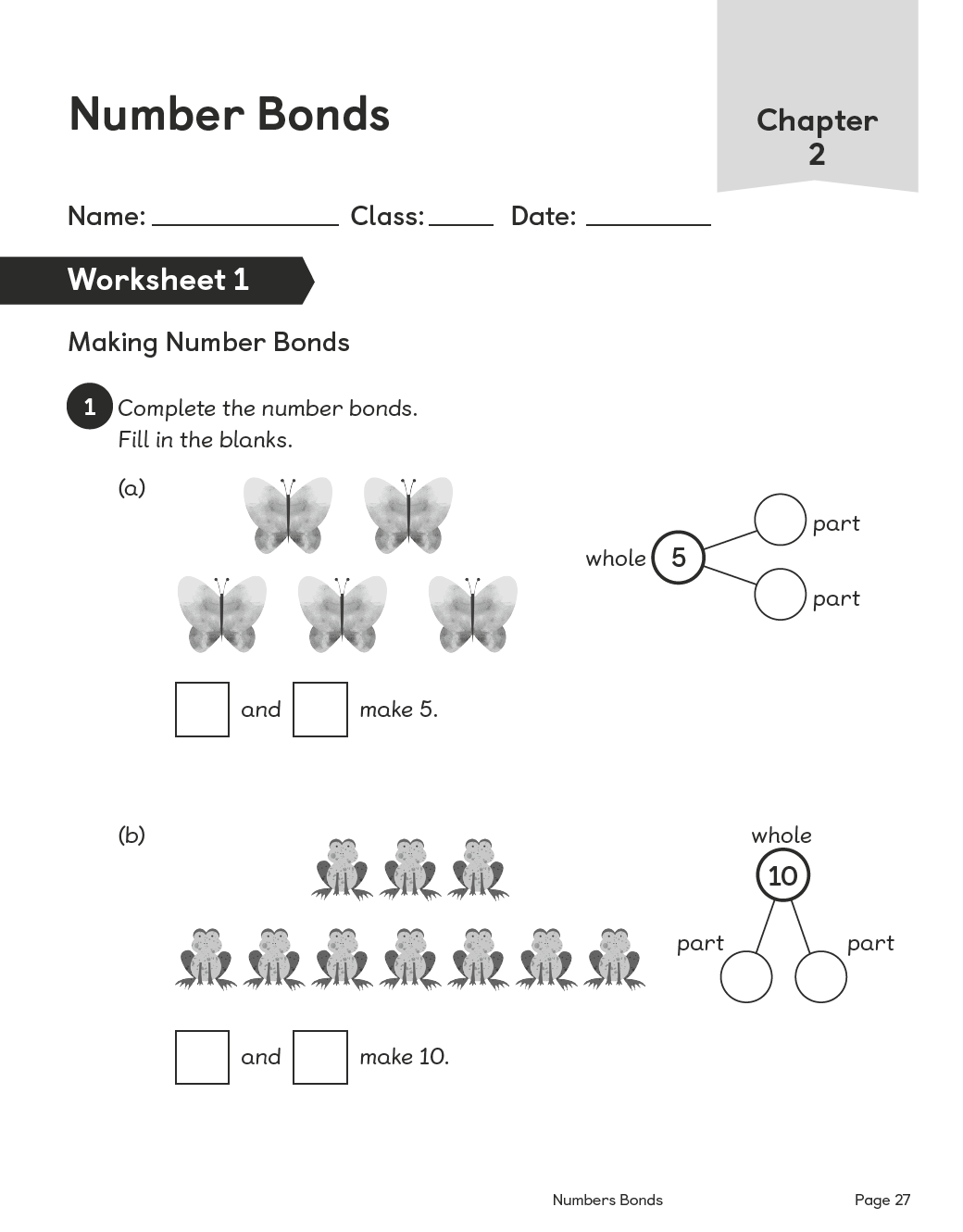
  Singapore Math Problems Worksheets

---

  Algebra 2 Factoring Worksheet

---

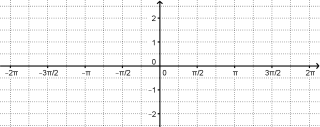
  Trigonometric Grid

---

  Unit Circle with Tangent

---

What is a linear equation?

A linear equation is an algebraic equation that represents a straight line on a graph. It consists of variables raised to the first power, without any exponents or roots. The general form of a linear equation is typically written as y = mx + b, where m represents the slope of the line and b represents the y-intercept.

How do you solve a linear equation algebraically?

To solve a linear equation algebraically, you need to isolate the variable by performing inverse operations. Start by simplifying both sides of the equation by distributing and combining like terms. Then, use inverse operations such as addition, subtraction, multiplication, and division to get the variable on one side of the equation and the constants on the other side. Continue solving for the variable until you find the solution that satisfies the equation.

How do you solve a linear equation graphically?

To solve a linear equation graphically, graph both the equations on the same coordinate plane. The solution will be the point where the two lines intersect. The x-coordinate of the point of intersection is the solution to the equation. If the lines are parallel and do not intersect, then there is no solution. If the lines coincide, then there are infinitely many solutions.

What is the slope-intercept form of a linear equation?

The slope-intercept form of a linear equation is y = mx + b, where m represents the slope of the line and b represents the y-intercept, the point where the line intersects the y-axis. This form can be used to graph linear equations easily and make predictions about the relationship between variables.

How do you find the slope and y-intercept from a linear equation in slope-intercept form?

To find the slope and y-intercept from a linear equation in slope-intercept form (y = mx + b), the slope is represented by the coefficient "m" of the x-term, while the y-intercept is the constant term "b". The slope indicates the rate of change of the line, or how steep it is, while the y-intercept is the point where the line crosses the y-axis.

How do you convert a linear equation from standard form to slope-intercept form?

To convert a linear equation from standard form (Ax + By = C) to slope-intercept form (y = mx + b), isolate the variable y on one side of the equation by solving for y. Start by subtracting Ax from both sides to get By = -Ax + C. Then, divide by B to get y = -(A/B)x + C/B, which can be simplified to y = mx + b, where m is the slope (-A/B) and b is the y-intercept (C/B).

How do you convert a linear equation from point-slope form to slope-intercept form?

To convert a linear equation from point-slope form (y - y1 = m(x - x1)) to slope-intercept form (y = mx + b), you need to solve for y. First, distribute the slope, denoted by m, to the x term inside the parentheses. Then, rewrite the equation by adding y1 to both sides to isolate y on one side. The result will be the equation in slope-intercept form, with the slope being m and the y-intercept being the constant term b.

How do you find the x-intercept and y-intercept of a linear equation?

To find the x-intercept of a linear equation, you set y=0 and solve for x. This gives you the point where the line crosses the x-axis. To find the y-intercept, you set x=0 and solve for y, giving you the point where the line crosses the y-axis. These intercepts represent where the line intersects each axis, helping you understand the behavior of the linear equation in a graphical context.

How do you write an equation of a line given a slope and a point on the line?

To write an equation of a line given a slope (m) and a point (x?, y?) on the line, you can use the point-slope form of a linear equation: y - y? = m(x - x?). Plug in the given values of the slope and the point into the equation, and then simplify and rearrange the equation to put it in slope-intercept form (y = mx + b) if required. This will give you the equation of the line passing through the given point with the specified slope.

How do you determine if two linear equations are parallel or perpendicular?

Two linear equations are parallel if their slopes are equal. To determine this, compare the coefficients of the variables in both equations - if they are the same, the lines are parallel. On the other hand, two linear equations are perpendicular if the product of their slopes is -1. To find this, calculate the slopes of both equations by putting them in the slope-intercept form (y = mx + b) and then take the negative reciprocal of one of the slopes. If the result is the slope of the other equation, then the lines are perpendicular.