Graphing Systems of Equations Worksheet

Are you a math teacher or student looking for a helpful resource to practice graphing systems of equations? Look no further! This blog post will introduce you to a graphing systems of equations worksheet that will allow you to deepen your understanding of this topic through practical exercises and real-world scenarios. Whether you are new to graphing systems of equations or just need some additional practice, this worksheet will provide you with the perfect opportunity to sharpen your skills and gain confidence in solving these types of problems.

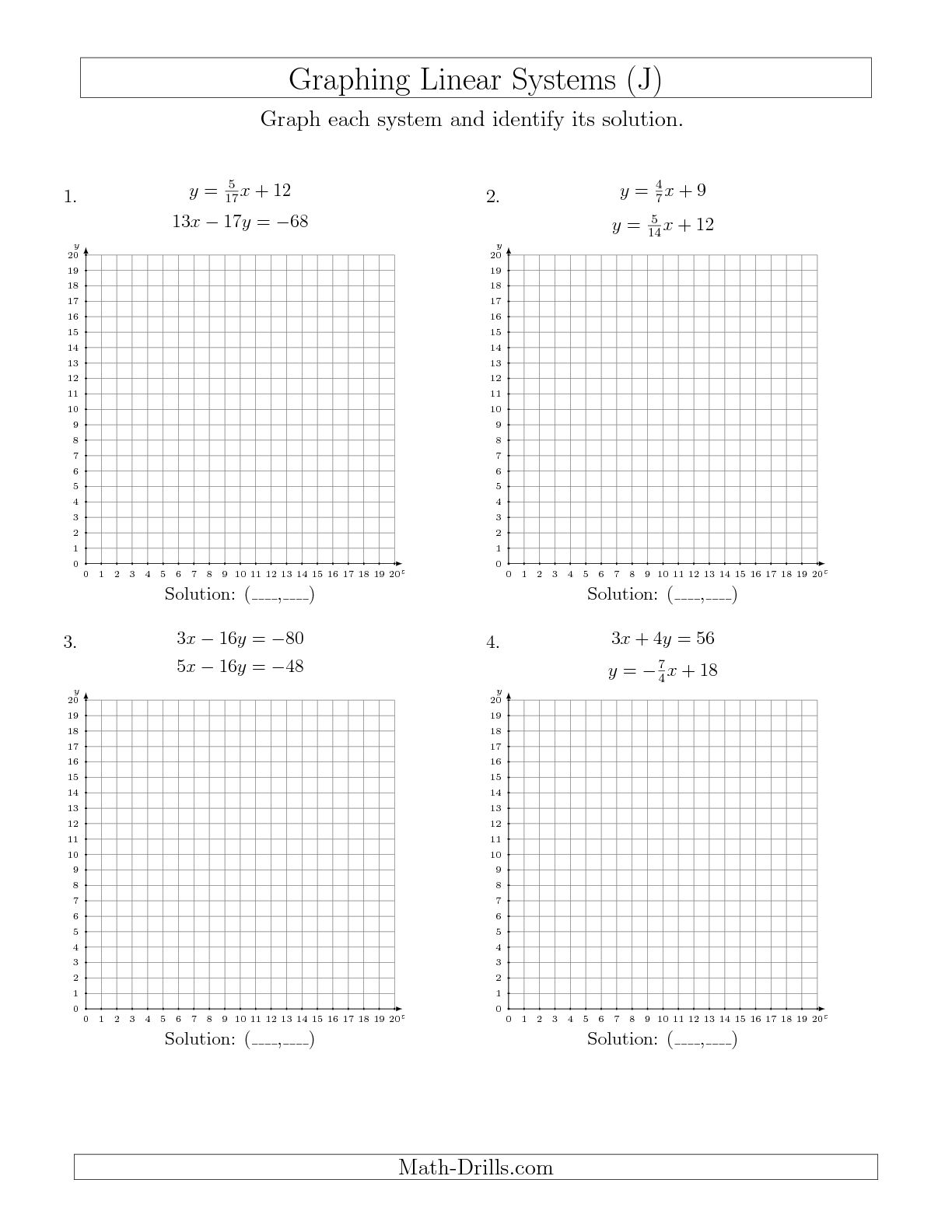
  Solving Systems of Linear Equations by Graphing

---

  Graphing Linear Inequalities Blank Worksheet

---

  Systems of Linear Equations by Graphing Worksheet

---

  Graphing Systems of Equations Worksheet Answers

---

  Graphing Linear Equations Worksheet

---

  Graphing Linear Inequalities Worksheet

---

  Graphing Equation Using Table of Values Worksheet

---

  Graphing Linear Inequalities Worksheet

---

  Graphing Motion Worksheet

---

  Solving Systems of Equations by Graphing Worksheets

---

  Graphing Lines Kuta Software Infinite Algebra 1 Answers Key

---

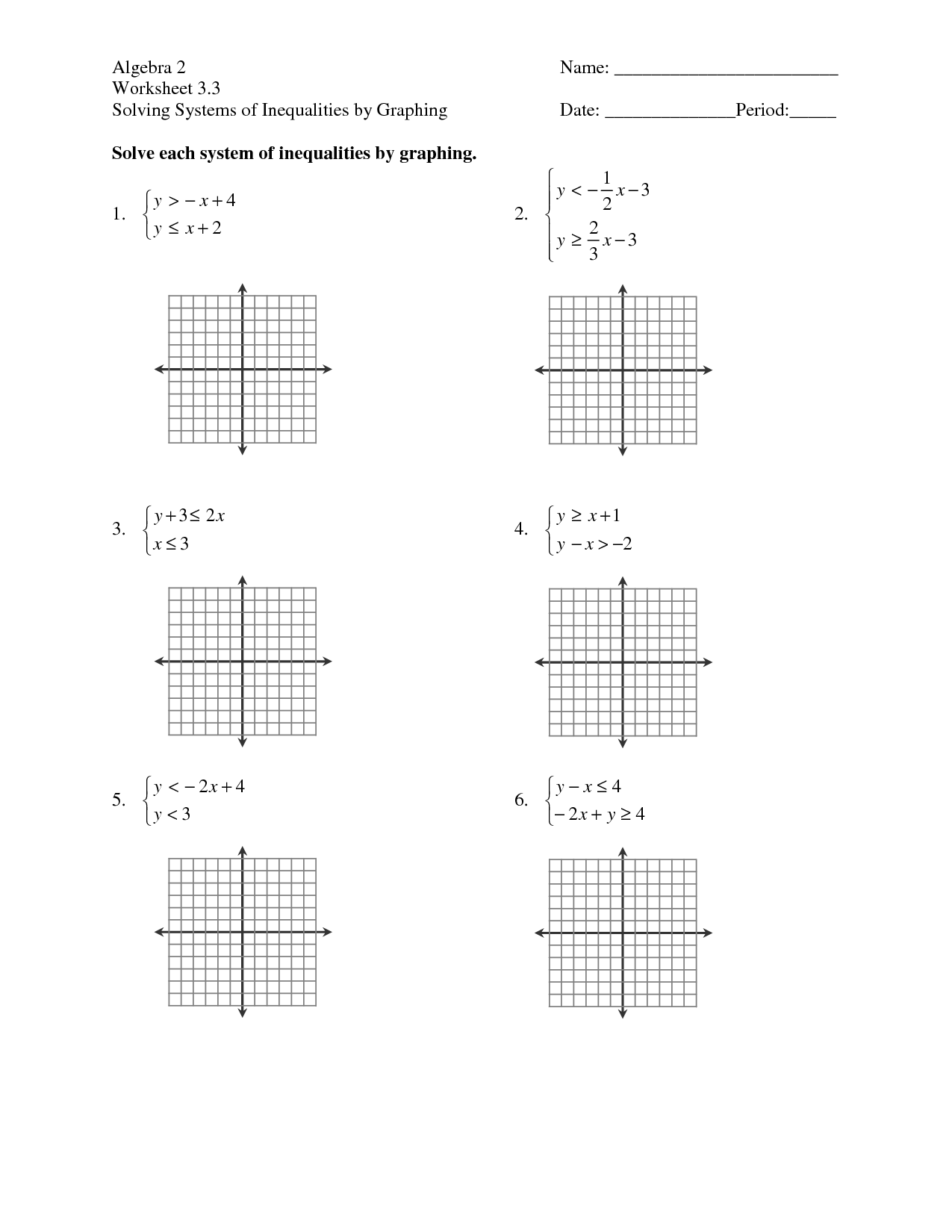
  Solving Systems of Inequalities by Graphing Worksheets

---

  Graphing Linear Inequalities Worksheet

---

What is a system of equations?

A system of equations is a collection of two or more equations that are analyzed together to find a common solution. The variables in the equations represent unknown values, and the goal is to find values that satisfy all of the equations simultaneously. Solving a system of equations involves determining the values of the variables that make all the equations true at the same time.

What is the purpose of graphing a system of equations?

Graphing a system of equations helps to visually represent the relationship between the equations and identify points where they intersect, which are the solutions to the system. It allows for a clear representation of the possible solutions and helps in understanding the behavior of the system, making it easier to solve for the unknown variables in a more intuitive way.

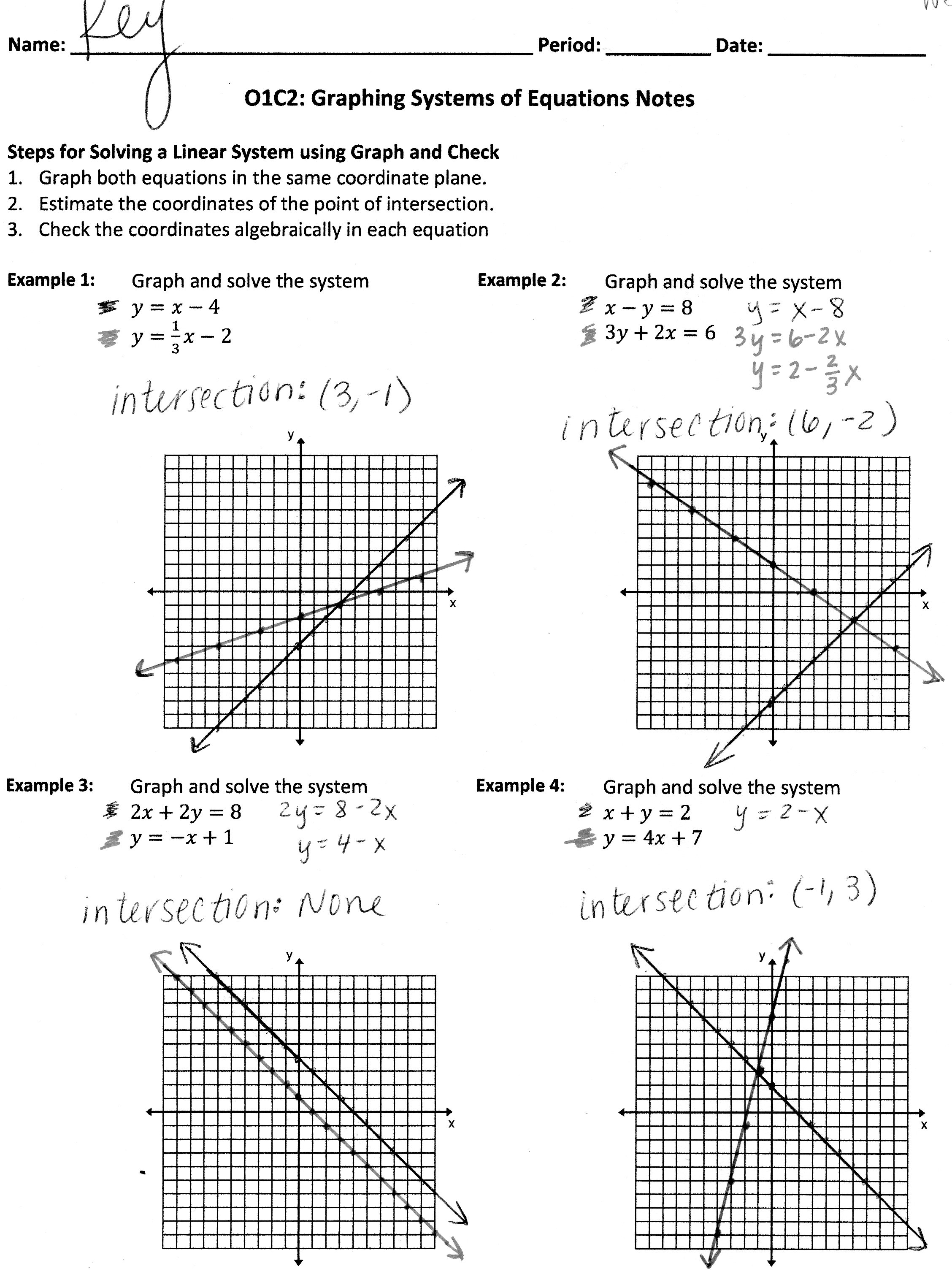
How can you determine the solution to a system of equations by graphing?

To determine the solution to a system of equations by graphing, you first graph each equation on the same coordinate plane. The point where the graphs intersect represents the solution to the system of equations, as it is the point that satisfies both equations simultaneously. If the graphs do not intersect, it means there is no solution to the system of equations.

What does it mean if the graphs of two equations intersect at a single point?

When the graphs of two equations intersect at a single point, it means that this point is the solution to both equations simultaneously. In other words, the x and y values of the point of intersection satisfy both equations, showing where the two lines meet on a coordinate plane.

What does it mean if the graphs of two equations are parallel?

If the graphs of two equations are parallel, it means that the lines represented by these equations have the same slope and will never intersect, no matter how far they are extended. This indicates that the equations have different y-intercepts but maintain a constant, consistent relationship between their x and y values.

Can the graphs of two equations ever be coincident? What does this mean?

Yes, the graphs of two equations can be coincident, which means they overlap perfectly and represent the same line or shape. This indicates that the two equations have the same solutions and are essentially equivalent, showing that they are representing the same relationship between variables on the graph.

How can you graph a system of equations with three variables?

To graph a system of equations with three variables, you would typically need to transition from a visual graph to a more abstract method due to the challenges of representing three dimensions on a 2D surface. One common approach is to use technology to plot points in a 3D space, such as using a graphing calculator or software like GeoGebra. By plotting the solutions where the equations intersect, you can visualize the relationship between the three variables in the system of equations. Additionally, you can also represent the system of equations using parametric equations and plot their solutions on a 3D graph.

Can a system of equations have no solution? If so, what does this look like on a graph?

Yes, a system of equations can have no solution if the equations represent parallel lines that do not intersect. This means that the lines are of the same slope but different y-intercepts, indicating that they never cross each other. On a graph, this scenario would show two distinct, non-intersecting lines running parallel to each other.

When graphing a system of equations, what is the significance of the x and y axes?

The x and y axes in a graph of a system of equations represent the variables in the equations. The x-axis typically represents the independent variable and the y-axis represents the dependent variable. By plotting points on the coordinate plane where the x and y values satisfy the equations in the system, the intersection point indicates the solution to the system of equations. The x and y values of the intersection point represent the specific values that satisfy all the equations in the system simultaneously, providing a graphical representation of the solution.

How can you use the properties of the graph to determine the number of solutions to a system of equations?

You can determine the number of solutions to a system of equations by examining the graphical representation of the equations. If the lines representing the equations intersect at a single point, then there is one unique solution to the system. If the lines are parallel and do not intersect at any point, then there are no solutions. Lastly, if the lines coincide and overlap each other, then there are infinitely many solutions to the system of equations.