Graphing Quadratic Equations Worksheet
Are you a high school student or a math enthusiast looking to strengthen your skills in graphing quadratic equations? If so, you've come to the right place. Our graphing quadratic equations worksheet is designed to provide you with ample practice in mastering this fundamental concept of algebra.
Table of Images 👆
- Quadratic Functions Algebra 2 Worksheets
- Graphing Quadratics Vertex Form Worksheet
- Solving Quadratic Equations by Completing the Square
- Cubic Equation Graph
- Input Output Table Blank Worksheet
- Solve Quadratic Equation Calculator
- Kimber Model 82 Exploded-View
- Polynomial Long Division Worksheet
- Kindergarten Map Skills Worksheets
- Special Factoring Patterns Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
What is a quadratic equation?
A quadratic equation is a mathematical equation of the form ax^2 + bx + c = 0, where x represents an unknown variable, and a, b, and c are constants with a not equal to zero. Quadratic equations generally have two solutions, which can be found using the quadratic formula or by factoring. They often represent parabolic curves when graphed.
How do you determine the vertex of a quadratic equation?
To determine the vertex of a quadratic equation in the form of y = ax^2 + bx + c, you can use the formula x = -b/2a to find the x-coordinate of the vertex. Once you have the x-coordinate, you can plug it back into the original equation to find the y-coordinate. The vertex is then represented as (x, y).
What is the axis of symmetry of a quadratic equation?
The axis of symmetry of a quadratic equation is a vertical line that passes through the vertex of the parabola represented by the equation. It divides the parabola into two symmetrical halves. The equation of the axis of symmetry is x = -b/(2a) in the standard form of a quadratic equation, y = ax^2 + bx + c.
How do you find the x-intercepts (zeros) of a quadratic equation?
To find the x-intercepts (zeros) of a quadratic equation, set the equation equal to zero and solve for x by factoring, using the quadratic formula, or completing the square. The x-intercepts are the points where the graph of the quadratic equation crosses the x-axis, and they represent the values of x where the equation equals zero.
How do you determine the direction of the parabola in a quadratic equation?
To determine the direction of the parabola in a quadratic equation, look at the coefficient of the squared term (x^2). If the coefficient is positive, the parabola opens upwards, forming a "U" shape. If the coefficient is negative, the parabola opens downwards, forming an upside-down "U" shape. This information helps you visualize the direction in which the parabola curves.
What is the significance of the discriminant in a quadratic equation?
The discriminant in a quadratic equation is significant because it helps determine the nature of the roots of the equation. By calculating the discriminant, which is denoted as "Δ" and equals b^2 - 4ac in the quadratic formula ax^2 + bx + c = 0, you can determine if the equation has two distinct real roots (Δ > 0), two complex roots (Δ < 0), or one real root (Δ = 0). This information is crucial in understanding the behavior and solutions of quadratic equations.
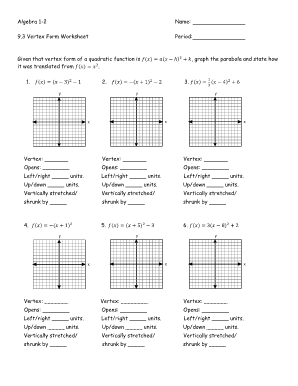
How can you use the vertex form of a quadratic equation to graph it?
To graph a quadratic equation using the vertex form \(y = a(x-h)^2 + k\), you first identify the vertex point \(h, k\). The vertex represents the turning point of the parabola. Next, plot the vertex on the coordinate plane. The value of \(a\) tells you whether the parabola opens upwards (\(a > 0\)) or downwards (\(a < 0\)). From the vertex, you can use the symmetry of the parabola to plot additional points on both sides of the vertex. By connecting these points, you can sketch the graph of the quadratic equation.
How do you use the standard form of a quadratic equation to identify key points on its graph?
The standard form of a quadratic equation is expressed as y = ax^2 + bx + c, where a, b, and c are constants. To identify key points on the graph of the quadratic equation, you can look at the values of these constants. The coefficient "a" tells you whether the parabola opens upwards or downwards, with a > 0 indicating an upward opening parabola and a < 0 indicating a downward opening parabola. The axis of symmetry is given by the equation x = -b/2a, and the vertex of the parabola is located at (x, y) where x is the axis of symmetry and y is the value of y when x is substituted into the equation. The y-intercept is at c, and you can find the x-intercepts by solving the quadratic equation for y = 0. These key points give you a good understanding of the shape and position of the graph of the quadratic equation.
What is the relation between the graph of a quadratic equation and the solutions it represents?
The graph of a quadratic equation represents a parabola, which can have either zero, one, or two x-intercepts depending on the solutions of the equation. If the parabola intersects the x-axis at two points, it means the equation has two real solutions. If the parabola touches the x-axis at one point, it means the equation has one real solution (a repeated root). And if the parabola does not intersect the x-axis at all, it means the equation has no real solutions. In summary, the relationship between the graph of a quadratic equation and the solutions it represents is that the number and nature of the solutions are directly related to the x-intercepts of the parabolic graph.
How can you determine the minimum or maximum point of a quadratic equation?
To determine the minimum or maximum point of a quadratic equation in the form of y = ax^2 + bx + c, you can use the formula x = -b / 2a to find the x-coordinate of the vertex. Once you have the x-coordinate of the vertex, substitute it back into the equation to find the y-coordinate. If the coefficient of the x^2 term (a) is positive, the parabola opens upwards, and the vertex represents the minimum point. If a is negative, the parabola opens downwards, and the vertex represents the maximum point.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





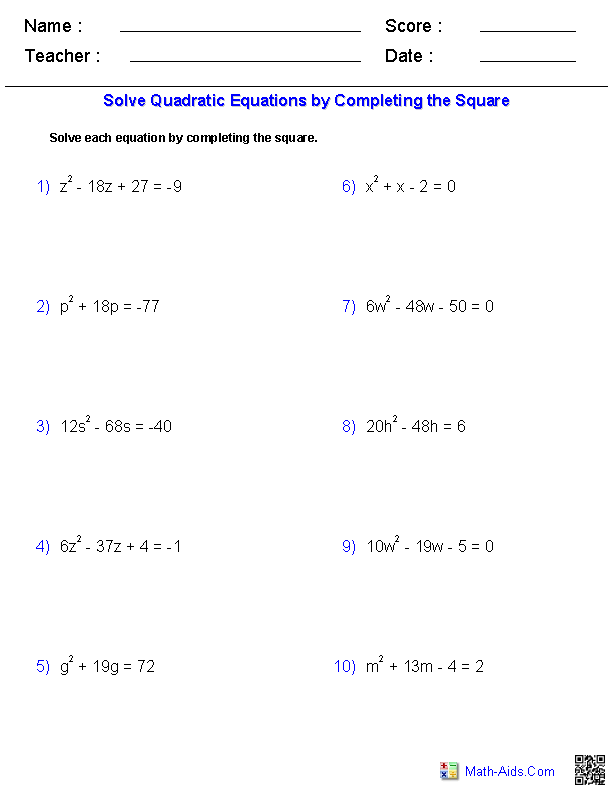
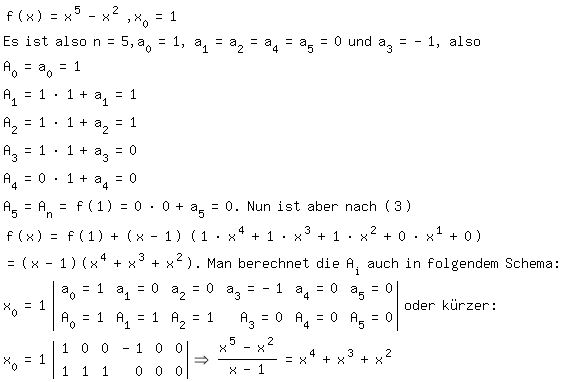















Comments