Graphing Equations Worksheet

A graphing equations worksheet is a valuable tool for students learning how to plot and analyze mathematical functions. Designed to provide practice and reinforcement, these worksheets are perfect for students who want to improve their skills in graphing.

  Graphing Equation Using Table of Values Worksheet

---

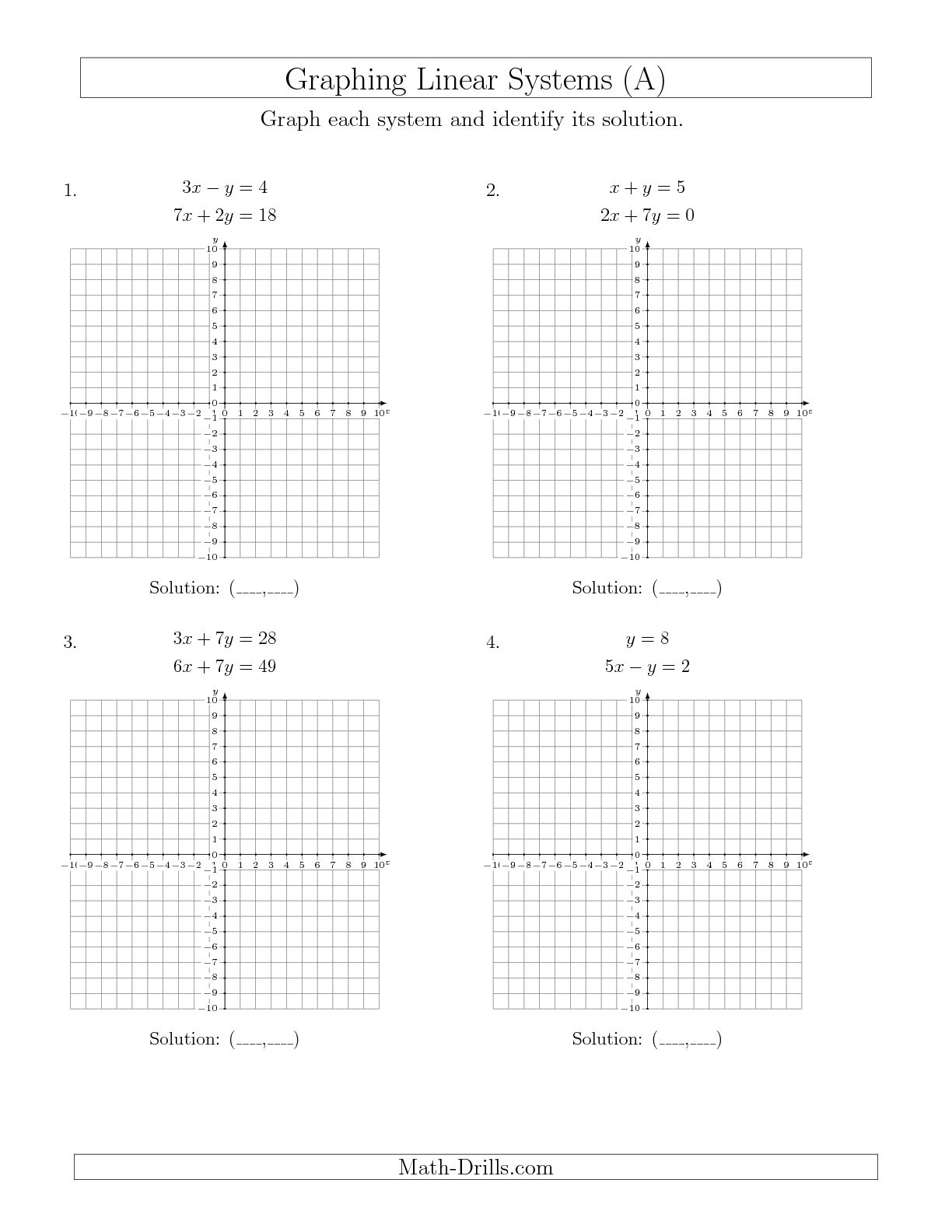
  Solving Systems of Linear Equations by Graphing

---

  Graphing Linear Equations Worksheet

---

  Graphing Quadratic Equations Finding the Vertex

---

  Algebra 1 Linear Equation Worksheets

---

  Simultaneous Equations Worksheets and Answers

---

  Coordinate Plane Worksheets 6th Grade

---

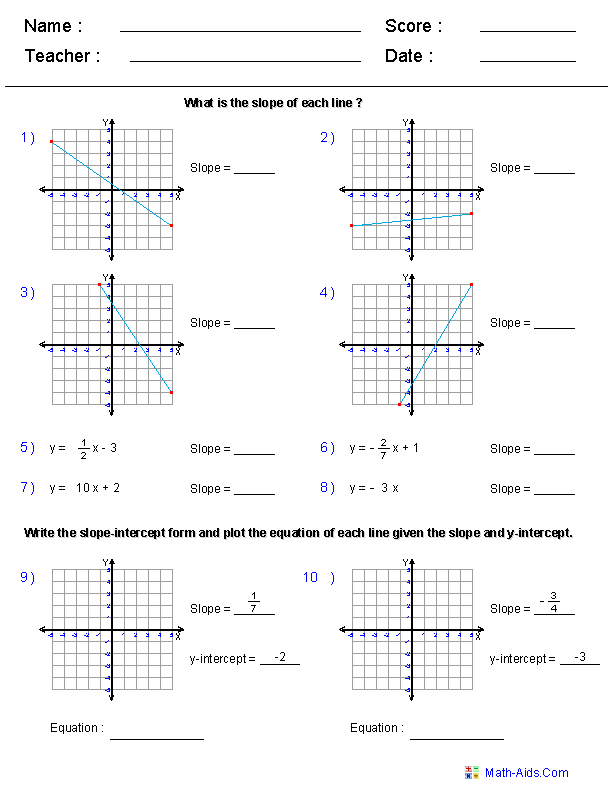
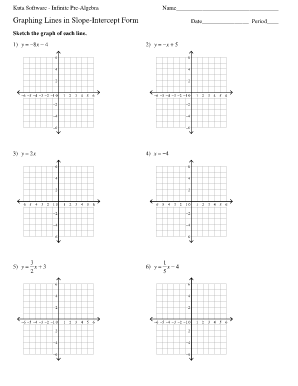
  Graph Slope-Intercept Form Worksheet Kuta

---

  Pre-Algebra Equations Worksheets

---

  Algebra Equations Word Problems Worksheets

---

  Inverse Functions Algebra 1 Worksheet

---

  6th Grade Algebra Equations Worksheets

---

  7th Grade Math Worksheets

---

What is the purpose of graphing equations?

The purpose of graphing equations is to visually represent the relationship between variables and understand how one variable changes in response to changes in another variable. Graphs provide a clear and concise way to analyze and interpret mathematical equations, allowing us to identify patterns, trends, and key features of the relationships being studied. They help in making predictions, solving problems, and making decisions based on the information provided by the graph.

How do you determine the x-intercept of a graphed equation?

To determine the x-intercept of a graphed equation, you need to look for the point where the graph intersects the x-axis. This point corresponds to the value of x when y equals zero. In other words, it is the point where the function crosses the x-axis, and the y-coordinate is zero. To find the x-intercept algebraically, you can set y equal to zero in the equation and solve for the values of x.

How do you determine the y-intercept of a graphed equation?

To determine the y-intercept of a graphed equation, you need to find the point where the graph intersects the y-axis. This point will have an x-coordinate of 0. By substituting x=0 into the equation, you can solve for the y-coordinate, which represents the y-intercept of the graph.

What is the slope of a line on a graphed equation?

The slope of a line on a graphed equation represents the rate at which the line is rising or falling. It is calculated as the change in the y-values divided by the change in the x-values between two points on the line. The slope is denoted by the letter "m" in the equation y = mx + b, where "m" is the slope and "b" is the y-intercept.

How do you identify parallel lines on a graphed equation?

You can identify parallel lines on a graphed equation by looking for lines that have the same slope. Parallel lines have the same slope but different y-intercepts. So, if you have two lines on a graph with the same slope, they are parallel to each other.

How do you identify perpendicular lines on a graphed equation?

Perpendicular lines on a graphed equation can be identified by looking at their slopes. Perpendicular lines have slopes that are negative reciprocals of each other. This means that if one line has a slope of m, the line perpendicular to it will have a slope of -1/m. By calculating the slopes of the lines and confirming that they are negative reciprocals, you can determine if the lines are perpendicular on the graph.

How do you determine the domain of a graphed equation?

To determine the domain of a graphed equation, you need to observe the x-values that are covered by the graph. The domain comprises all possible x-values for which the equation is defined. In other words, you identify the leftmost and rightmost points on the graph to establish the range of x-values that the equation covers. Any gaps, asymptotes, or undefined points on the graph indicate restrictions on the domain.

How do you determine the range of a graphed equation?

To determine the range of a graphed equation, you look at the vertical spread of the graph. The range is the set of all possible output values of the function, so you need to find the lowest and highest points on the y-axis that the graph reaches. The range includes all y-values between these minimum and maximum points. In other words, it is the interval of y-values that correspond to the function's output.

How do you identify symmetry on a graphed equation?

To identify symmetry on a graphed equation, you can check for symmetry across the x-axis, y-axis, or origin. If a function is even, it is symmetric across the y-axis, meaning that replacing x with -x results in the same function. If a function is odd, it is symmetric across the origin, meaning that replacing x with -x and y with -y results in the same function. Additionally, you can also check for symmetry across the line y=x, which is known as diagonal symmetry. If the function remains unchanged under these transformations, then it exhibits symmetry.

How can you use graphing to solve systems of equations?

Graphing systems of equations involves plotting the equations on a graph and finding the point where they intersect, which represents the solution to the system. Each equation is graphed as a line, and the point of intersection is where the x and y values satisfy both equations simultaneously. By visually analyzing the graphs, you can determine the point of intersection and thus find the solution to the system of equations.