Graph Transformations Worksheet

A graph transformations worksheet provides valuable practice and reinforcement for students learning about how different transformations affect the shape and position of graphs. This resource targets individuals studying algebra or pre-calculus, who are looking to solidify their understanding of graphing functions and how they can be adjusted and manipulated.

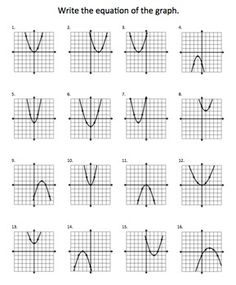
  Quadratic Function Graph Transformations Worksheet

---

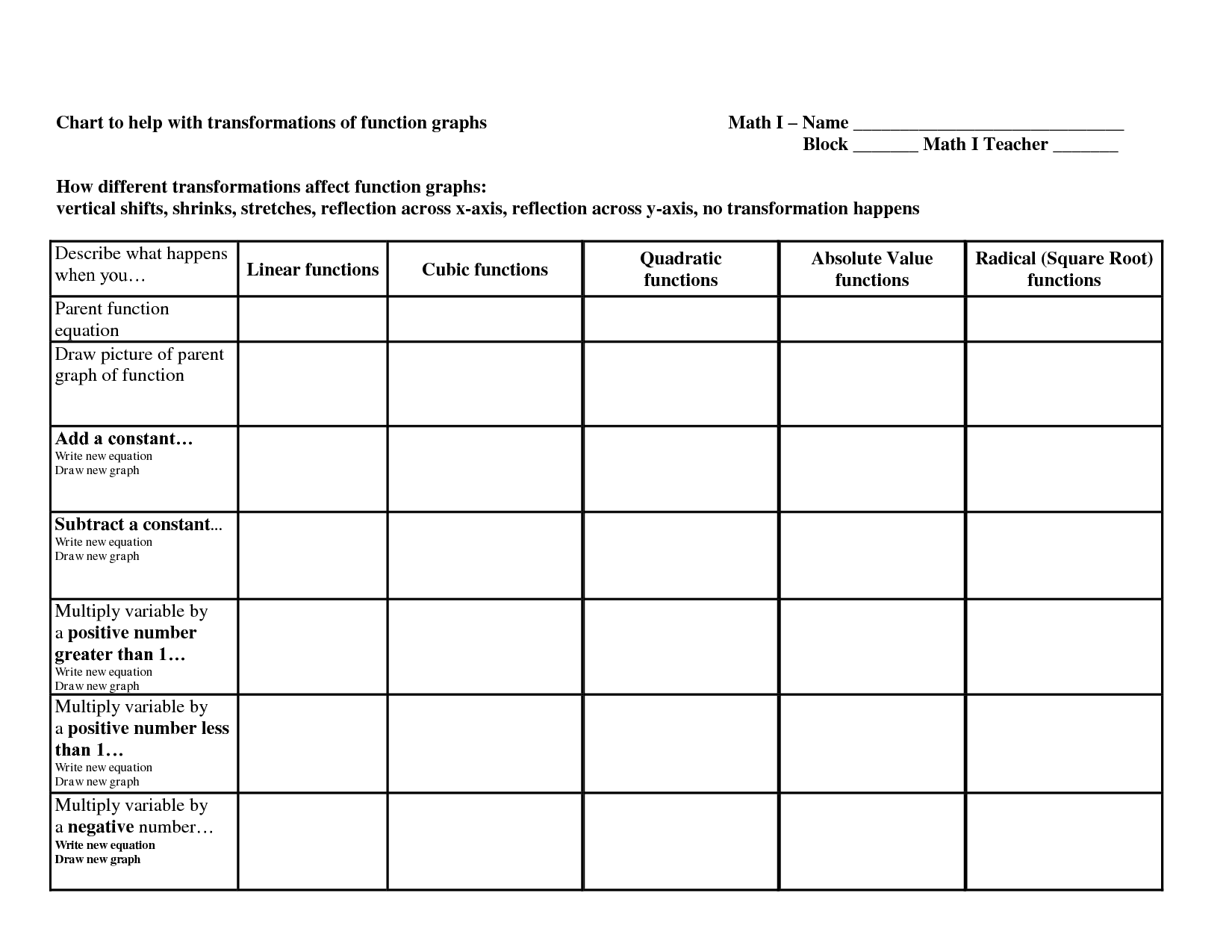
  Chart Graph Functions Transformations

---

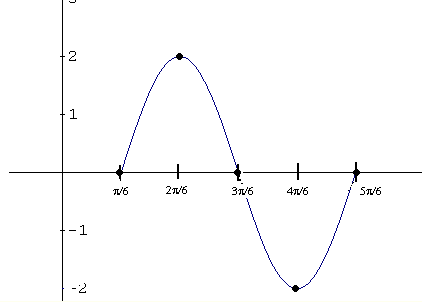
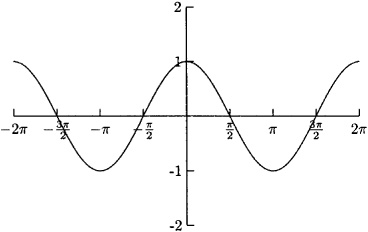
  Real Life Examples of Sine and Cosine Graphs

---

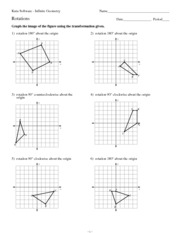
  Kuta Software Transformations Worksheets

---

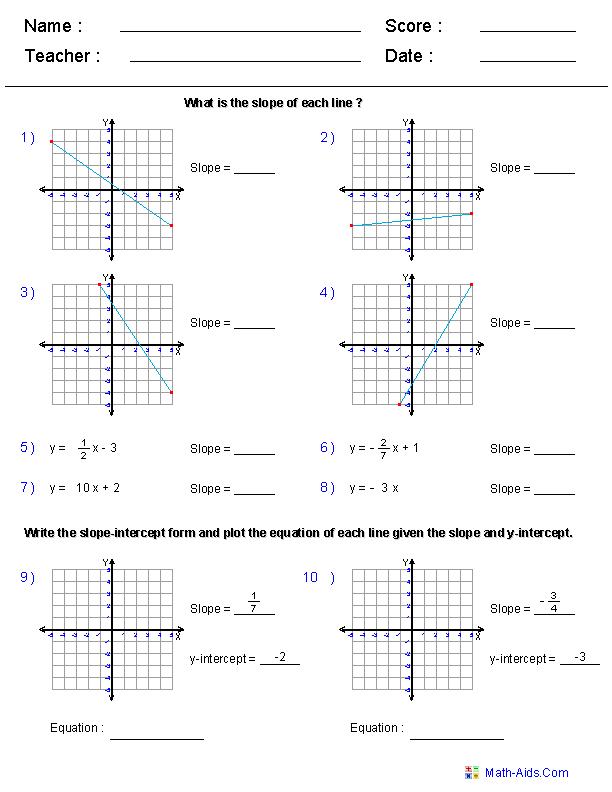
  These Linear Equations Worksheets

---

  Cos X Parent Function Graph

---

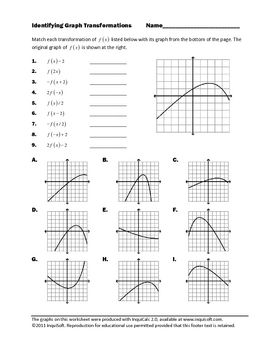
  Identifying Graph Transformations

---

  Inverse Functions Algebra 2 Worksheets

---

What are graph transformations?

Graph transformations are changes made to the shape or position of a graph, typically by applying operations such as translations, reflections, expansions, or compressions. These transformations alter the appearance of the graph while preserving its basic characteristics, allowing for a more intuitive understanding of how the function behaves under different adjustments.

How do you identify a graph transformation?

To identify a graph transformation, examine how the original function has been modified. Look for any changes to the equation such as shifts, stretches, compressions, reflections, or vertical/horizontal translations. These changes will affect the shape, size, and position of the graph compared to the original function. By analyzing these alterations, you can determine the graph transformation that has occurred.

What happens to the shape of a graph during a vertical translation?

During a vertical translation, the shape of a graph remains the same while the entire graph is shifted up or down vertically. This means the relationship between the x and y values remains consistent, but the position of the graph on the coordinate plane changes.

How is a horizontal reflection depicted on a graph?

A horizontal reflection on a graph is depicted by flipping the graph across the y-axis. This means that all points on the graph are mirrored across the y-axis, with points on the left side of the y-axis moving to the right side and vice versa. This reflection results in the graph being a mirror image of its original form with respect to the y-axis.

How does a vertical dilation affect the graph of a function?

A vertical dilation of a function changes the y-coordinates of the points on the graph, but not the x-coordinates. If the dilation factor is greater than 1, the graph is stretched vertically, making it appear taller. If the factor is between 0 and 1, the graph is compressed vertically, making it appear shorter. The shape and steepness of the graph remain the same, only the size along the y-axis is altered by the dilation.

How does a vertical compression impact the graph of a function?

A vertical compression of a function results in the graph being stretched vertically closer to the x-axis. This happens when the function is multiplied by a fraction that is between 0 and 1. The compression causes the y-values of the function to decrease, making the graph appear narrower and taller compared to the original function.

How does a horizontal translation change the graph of a function?

A horizontal translation shifts the graph of a function left or right without changing its shape. For a given function f(x), a horizontal translation by h units to the right can be represented by the function f(x - h), while a translation by h units to the left is represented by f(x + h). This shifts the entire graph of the function horizontally without affecting its vertical position or shape.

How does a horizontal dilation affect the graph of a function?

A horizontal dilation affects the graph of a function by compressing or stretching it horizontally. If the dilation factor is greater than 1, the graph will be stretched horizontally, making it wider. Conversely, if the dilation factor is between 0 and 1, the graph will be compressed horizontally, making it narrower. The vertical position of the graph remains the same, but the horizontal distance between points on the graph will change according to the dilation factor.

What happens to the graph of a function during a vertical reflection?

During a vertical reflection, the entire graph of the function is flipped upside down over the x-axis. This means that points above the x-axis move below it and vice versa, resulting in a reversal of the vertical direction of the graph. The shape and features of the graph remain the same, but the orientation changes to create a mirrored image across the x-axis.

What is the relationship between the original graph and the transformed graph after applying multiple transformations?

The relationship between the original graph and the transformed graph after applying multiple transformations is that the transformed graph is a result of sequentially applying each individual transformation to the original graph. Each transformation alters the original graph in a specific way, such as shifting, stretching, reflecting, or rotating it. The combination of these transformations results in a new graph that is a combination of all the individual changes made to the original graph.