Geometry Shapes Proportion Problems Worksheets
Geometry shapes proportion problems worksheets are a useful tool for students who are learning about the relationship between different shapes and their proportions. With these worksheets, students can practice identifying and comparing the sizes of various shapes, helping them to develop a solid understanding of geometric concepts.
Table of Images 👆
- Solving Proportions Worksheet
- Solving Proportions Worksheet
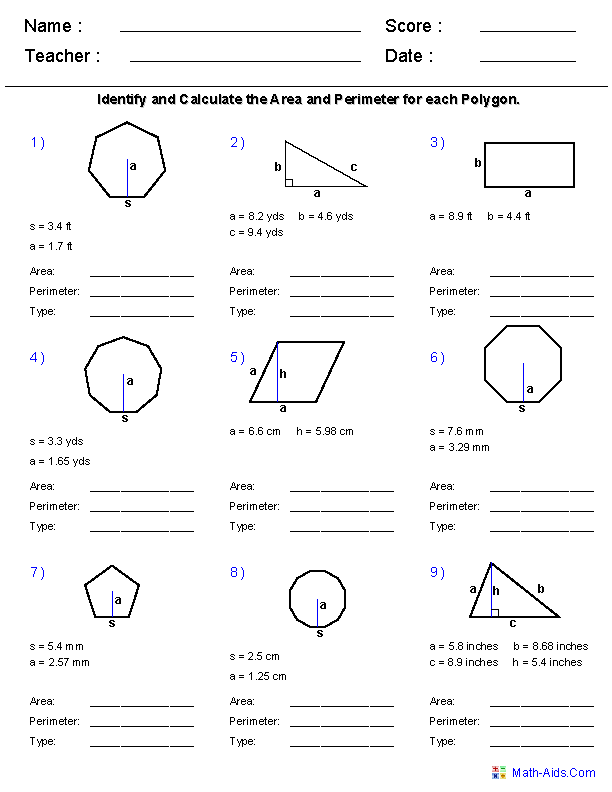
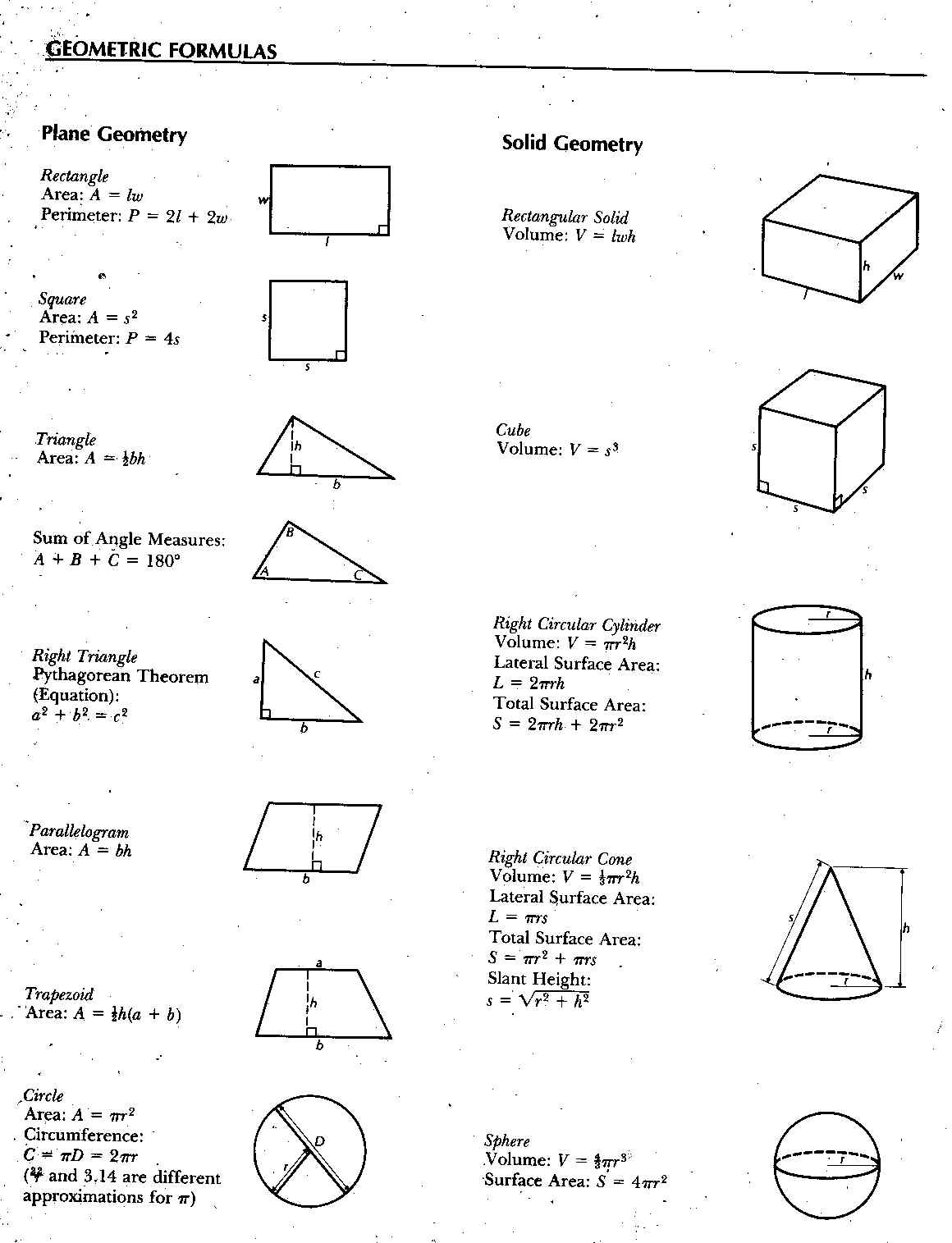
- Area and Perimeter Worksheets
- Equivalent Ratios Worksheets
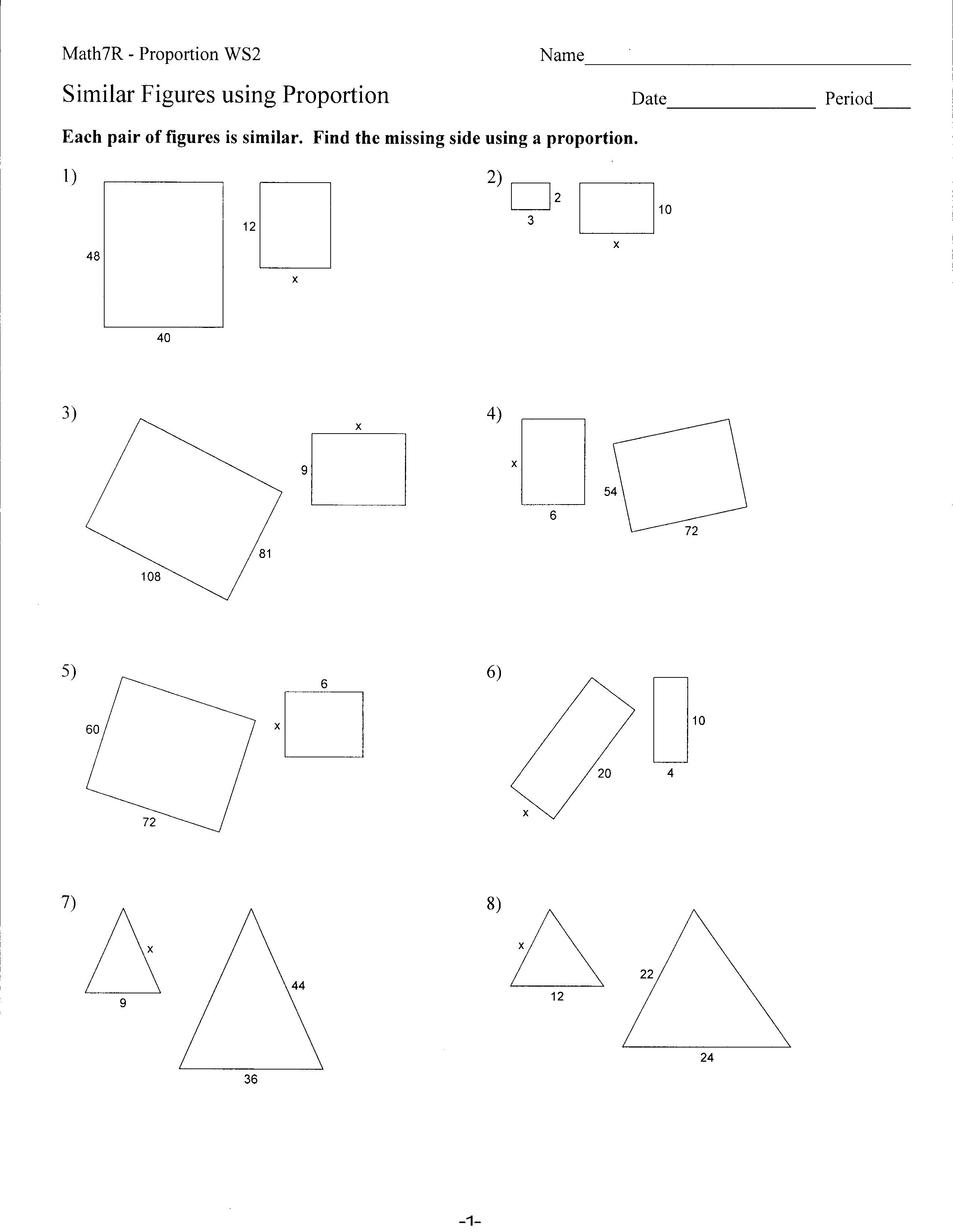
- Similar Figures and Proportions Worksheets
- Similar Figures 7th Grade Worksheets
- Solving Proportions Worksheet
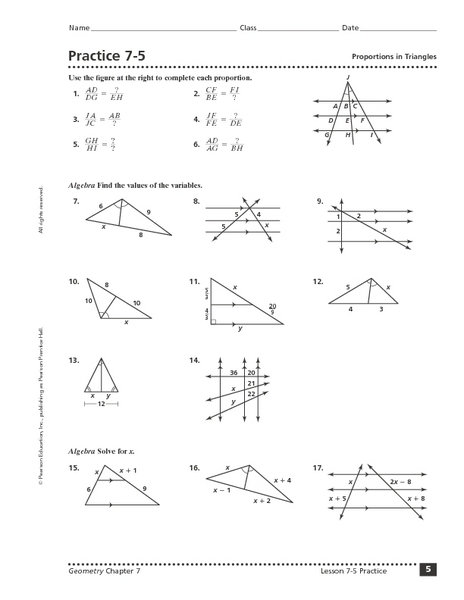
- Practice 7 5 Proportions in Triangles Answers
- Solving Proportions Worksheet
- Similar Figures and Proportions Worksheets
- Shapes Worksheets 1st Grade
- Triangular Prism Surface Area Worksheet
- Proportion and Scale Drawing Worksheet
More Shape Worksheets
Color and Shape Review WorksheetsDrawing Shapes Worksheets
Nets of Shapes Worksheet
Sail Boat Printable Shapes Worksheets
Drawing Shapes Worksheets Kindergarten
Plane Shapes Worksheets for Kindergarten
3D Shapes Worksheets Printables Kindergarten
Preschool Cut and Paste Shape Worksheets
Regular Polygon Shapes Worksheet
Preschool Shape Recognition Worksheets
What is the definition of proportion in geometry?
Proportion in geometry refers to the relationship between quantities or measurements, typically expressed as a ratio or fraction. In a geometric context, proportions are used to compare corresponding sides of similar figures or to determine the dimensions of shapes based on their ratios. They play a crucial role in various geometric concepts, such as similarity, scale factor, and dimensional consistency.
How can we determine if two shapes are proportional?
Two shapes are proportional if their corresponding sides are in the same ratio. To determine if two shapes are proportional, simply compare the ratios of corresponding sides. If these ratios are equal, then the shapes are proportional. This means that when you enlarge or reduce one shape, the other shape will also enlarge or reduce by the same scale factor, maintaining their proportional relationship.
What is the formula for finding the ratio of corresponding sides?
The formula for finding the ratio of corresponding sides in similar triangles is to divide the length of a side in one triangle by the length of the corresponding side in the other triangle. This ratio remains constant for all pairs of corresponding sides in similar triangles and is a fundamental property of similarity.
How can we use proportions to solve for unknown side lengths?
To use proportions to solve for unknown side lengths, you can set up a ratio of corresponding side lengths in similar figures. By equating these ratios, you can create a proportion equation and solve for the unknown side length by cross multiplying. This method works particularly well when dealing with similar geometric shapes where corresponding sides are proportional to each other.
Can proportions be used to solve for unknown angle measures?
Yes, proportions can be used to solve for unknown angle measures in geometric problems. By setting up ratios of side lengths or angles within similar shapes, it is possible to create proportion equations that can help solve for unknown angle measures. This method is commonly used in geometry and trigonometry to find missing angles in various types of triangles or polygons.
How do we use proportions to solve for missing angles in similar triangles?
To use proportions to solve for missing angles in similar triangles, we first establish the corresponding sides are proportional in both triangles. Then, we set up a proportion comparing the corresponding sides that involve the missing angle we want to find. By solving this proportion, we can determine the value of the missing angle in the similar triangles. This technique works because in similar triangles, corresponding angles are congruent and corresponding sides are proportional.
What are some real-life applications of using proportions in geometry?
Proportions in geometry are commonly used in real-life applications such as map scaling, architectural design, and construction. For example, architects use proportions to accurately scale down building blueprints to fit on paper, ensuring that all dimensions are maintained correctly. Similarly, surveyors use proportions to scale distances on maps, allowing them to accurately represent real-world distances on smaller-scale drawings. Additionally, interior designers use proportions to ensure that furniture and decor elements are appropriately sized for a room's dimensions, creating a balanced and harmonious space.
What are the properties of shapes that remain the same when they are scaled proportionally?
When shapes are scaled proportionally, their corresponding angles remain the same, their sides increase or decrease in length by the same scale factor, and their overall shape and orientation are preserved. This means that the ratio of corresponding side lengths remains constant during the scaling process, ensuring that the shape maintains its similarity while changing in size.
How do we determine if three shapes are in proportion?
To determine if three shapes are in proportion, you need to compare the corresponding sides of the shapes. If the ratios of the corresponding sides of the shapes are equal, then the shapes are in proportion. This means that the sides are scaled versions of each other and maintain the same proportions. If the ratios are not equal, the shapes are not in proportion.
How can we use proportions to compare the areas or volumes of shapes?
Proportions can be used to compare the areas or volumes of shapes by setting up ratios that represent the dimensions of the shapes. For two-dimensional shapes, the areas are compared by squaring the corresponding side lengths and setting up a ratio. Similarly, for three-dimensional shapes, the volumes are compared by cubing the corresponding dimensions and setting up a ratio. By utilizing proportions, we can easily determine the relationship between the areas or volumes of different shapes and make comparisons based on their respective dimensions.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





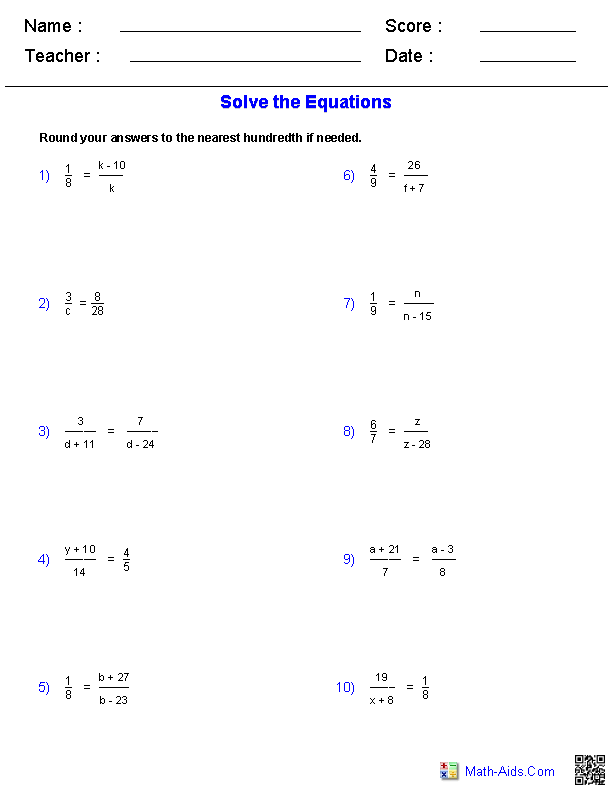




















Comments